
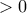 , ώστε
, ώστε  να δείξετε ότι:
να δείξετε ότι:![\displaystyle{\sqrt{\frac 23}\left(\sqrt[2018]{a}\ +\sqrt[2018]{b}\ + \sqrt[2018]{c}\hskip 0.05 in\right)
+\sqrt{a(1-b)+b(1-c)+c(1-a)\ }\geq\sqrt{6}.} \displaystyle{\sqrt{\frac 23}\left(\sqrt[2018]{a}\ +\sqrt[2018]{b}\ + \sqrt[2018]{c}\hskip 0.05 in\right)
+\sqrt{a(1-b)+b(1-c)+c(1-a)\ }\geq\sqrt{6}.}](/forum/ext/geomar/texintegr/latexrender/pictures/ce6d1f4897353ea2d9c18833fdeeac54.png)
Πηγή: (Aops) (Δεν έχει ανέβει κάποια λύση ακόμη).
Συντονιστές: achilleas, emouroukos, silouan
Καλησπέρα σε όλους.ΑΝΔΡΕΑΣ ΛΑΜΠΡΟΥ έγραψε: ↑Πέμ Ιουν 14, 2018 3:25 amΑν
, ώστε
να δείξετε ότι:
Πηγή: (Aops) (Δεν έχει ανέβει κάποια λύση ακόμη).
 πραγματικούς, ισχύει ότι
πραγματικούς, ισχύει ότι  .
. .
. , οπότε
, οπότε  . Τότε, με αντικατάσταση, προκύπτει
. Τότε, με αντικατάσταση, προκύπτει  και άρα αρκεί
και άρα αρκεί 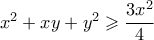 ή αλλιώς
ή αλλιώς  , που ισχύει, γιατί
, που ισχύει, γιατί  .
. (η προς απόδειξη ανισότητα είναι συμμετρική, οπότε μπορούμε να υποθέσουμε κάτι τέτοιο).
(η προς απόδειξη ανισότητα είναι συμμετρική, οπότε μπορούμε να υποθέσουμε κάτι τέτοιο).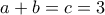 , είναι προφανώς
, είναι προφανώς  .
. .
.![\sqrt{\dfrac{2}{3}}(\sqrt[2018]{a}+\sqrt[2018]{b}+\sqrt[2018]{c})+\sqrt{a+b+c-ab-bc-ca} \geqslant \sqrt{\dfrac{2}{3}}(2+\sqrt[2018]{c})+\dfrac{(c-1)\sqrt{3}}{2}=M \sqrt{\dfrac{2}{3}}(\sqrt[2018]{a}+\sqrt[2018]{b}+\sqrt[2018]{c})+\sqrt{a+b+c-ab-bc-ca} \geqslant \sqrt{\dfrac{2}{3}}(2+\sqrt[2018]{c})+\dfrac{(c-1)\sqrt{3}}{2}=M](/forum/ext/geomar/texintegr/latexrender/pictures/5ca1232bbf2d0fe87ff16175d6ba7287.png) , οπότε αρκεί
, οπότε αρκεί  .
. , με
, με 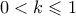 , μετά τις πράξεις, αρκεί
, μετά τις πράξεις, αρκεί  (1).
(1). , οπότε
, οπότε  , άρα έχουμε
, άρα έχουμε  , ό.έ.δ.
, ό.έ.δ.
![\sqrt[n]{x} \geqslant x \sqrt[n]{x} \geqslant x](/forum/ext/geomar/texintegr/latexrender/pictures/247507722b34507401643cf5915f3cb4.png) , για κάθε
, για κάθε  και
και  (πράγματι,
(πράγματι, ![x^n=x \cdot x^{n-1} \leqslant x \Rightarrow \sqrt[n]{x} \geqslant x x^n=x \cdot x^{n-1} \leqslant x \Rightarrow \sqrt[n]{x} \geqslant x](/forum/ext/geomar/texintegr/latexrender/pictures/87f4abd14b0edcc8e523f39fdf24d0f8.png) ) έχουμε :
) έχουμε :![\sqrt{\dfrac{2}{3}}(\sqrt[2018]{a}+\sqrt[2018]{b}+\sqrt[2018]{c})+\sqrt{a+b+c-ab-bc-ca} \geqslant \sqrt{\dfrac{2}{3}}(1+b+c)+\dfrac{(a-1)\sqrt{3}}{2} \sqrt{\dfrac{2}{3}}(\sqrt[2018]{a}+\sqrt[2018]{b}+\sqrt[2018]{c})+\sqrt{a+b+c-ab-bc-ca} \geqslant \sqrt{\dfrac{2}{3}}(1+b+c)+\dfrac{(a-1)\sqrt{3}}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/1bccac45e1d4919961c485061071de6e.png) , οπότε αρκεί
, οπότε αρκεί  ή ισοδύναμα
ή ισοδύναμα  , που προφανώς ισχύει, αφού
, που προφανώς ισχύει, αφού 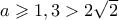 .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες