
Να δειχθεί ότι

Πότε ισχύει η ισότητα;
Ας την αφήσουμε για μαθητές μέχρι να φάμε το αρνί.
Συντονιστές: achilleas, emouroukos, silouan


Καλημέρα κύριε Σταύρο!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 06, 2018 11:46 amΕστω
Να δειχθεί ότι
Πότε ισχύει η ισότητα;
Ας την αφήσουμε για μαθητές μέχρι να φάμε το αρνί.
 . Τότε,
. Τότε,  .
. .
. , από την Cauchy-Schwarz.
, από την Cauchy-Schwarz. .
. . Τότε, αρκεί
. Τότε, αρκεί  (ξαναεφαρμόστηκε η Cauchy-Schwarz).
(ξαναεφαρμόστηκε η Cauchy-Schwarz). , που ισχύει.
, που ισχύει. ,
,  και
και  .
. .
.Καλημέρα Ορέστη.Ορέστης Λιγνός έγραψε: ↑Παρ Απρ 06, 2018 12:33 pmΚαλημέρα κύριε Σταύρο!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 06, 2018 11:46 amΕστω
Να δειχθεί ότι
Πότε ισχύει η ισότητα;
Ας την αφήσουμε για μαθητές μέχρι να φάμε το αρνί.
Έστω. Τότε,
.
Έτσι, η ανισότητα γράφεται.
Είναι, από την Cauchy-Schwarz.
Αρκεί λοιπόν.
Έστω. Τότε, αρκεί
(ξαναεφαρμόστηκε η Cauchy-Schwarz).
Η παραπάνω γράφεται, που ισχύει.
Η ισότητα ισχύει όταν ισχύει η ισότητα σε όλες τις παραπάνω ανισότητες, δηλαδή,
και
.
Από τα παραπάνω, παίρνουμε ότι η ισότητα ισχύει για.

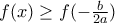


 και μετά σαν τριώνυμο
και μετά σαν τριώνυμο 

Πάνω κάτω όπως ο Ορέστης:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 06, 2018 1:21 pm[
Να σημειώσω ότι μου προέκυψε από άλλο πρόβλημα η γενικότερη
και η πρώτη απόδειξη που έδωσα ήταν με Λογισμό πολλών μεταβλητών.


Σιλουανέ εγώ θα έλεγα ότι και οι τρείς λύσεις βασίστηκαν στην κυρτότητα.silouan έγραψε: ↑Σάβ Απρ 07, 2018 7:22 pmΠάνω κάτω όπως ο Ορέστης:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 06, 2018 1:21 pm[
Να σημειώσω ότι μου προέκυψε από άλλο πρόβλημα η γενικότερη
και η πρώτη απόδειξη που έδωσα ήταν με Λογισμό πολλών μεταβλητών.
Από C-S έχουμε:
Ξανά όμως από C-S
Αφού το δεξί μέλος είναι ίσο με 1 έχουμε το ζητούμενο.




Απλά και μόνο για το Χριστός Ανέστη και σίγουρα για λόγους πλουραλισμού για τους μικρούς σε ηλικία συναδέλφους, όπως ο Ορέστης, αλλά και γενικώτερα, ας δούμε και την εκδοχή που ακολουθεί:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Απρ 06, 2018 11:46 amΕστωΝα δειχθεί ότι
. Πότε ισχύει η ισότητα;
 , να αποδειχθεί ότι:
, να αποδειχθεί ότι:  αρκεί
αρκεί ![1 + 3\left[ {2{x^2} + 2{{\left( {1 - z} \right)}^2} - {{\left( {x + 1 - z} \right)}^2}} \right] \geqslant 1 1 + 3\left[ {2{x^2} + 2{{\left( {1 - z} \right)}^2} - {{\left( {x + 1 - z} \right)}^2}} \right] \geqslant 1](/forum/ext/geomar/texintegr/latexrender/pictures/77ca130c37e92bb7b51608d4820822e9.png) , αρκεί
, αρκεί  αρκεί
αρκεί  που ισχύει, με την ισότητα εδώ να είναι αληθής όταν
που ισχύει, με την ισότητα εδώ να είναι αληθής όταν 
 , ισχύει όταν έχουμε το σύστημα:
, ισχύει όταν έχουμε το σύστημα:  και
και  που οδηγεί στην λύση
που οδηγεί στην λύση 
 Χρησιμοποιήθηκε η ανισότητα
Χρησιμοποιήθηκε η ανισότητα  όταν
όταν  Αυτή ως γνωστόν ισχύει ως ισότητα όταν
Αυτή ως γνωστόν ισχύει ως ισότητα όταν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες