Βρείτε όλους τους (x,y,z) τέτοιοι ώστε

με

(United Kingdom 1998)
Συντονιστές: achilleas, emouroukos, silouan




![\displaystyle{\bullet~ x+y+z\geq 3\sqrt[3]{xyz}\implies a\geq 3\sqrt[3]{a+2}\implies a^3-27a-54\geq 0 \stackrel{a>0}{\implies }a\geq 6.} \displaystyle{\bullet~ x+y+z\geq 3\sqrt[3]{xyz}\implies a\geq 3\sqrt[3]{a+2}\implies a^3-27a-54\geq 0 \stackrel{a>0}{\implies }a\geq 6.}](/forum/ext/geomar/texintegr/latexrender/pictures/409cb5058f9fb908a694874f6f07f3b4.png)
 και ισχύει παντού ισότητα. Άρα
και ισχύει παντού ισότητα. Άρα 
Ακόμα μια λύση:Τσιαλας Νικολαος έγραψε: ↑Παρ Φεβ 23, 2018 2:59 pmΔεν υπάρχει πουθενά λύση. Δεν το βρήκαμε κανείς.
Βρείτε όλους τους (x,y,z) τέτοιοι ώστε
με
(United Kingdom 1998)
 προκύπτει ότι υπάρχουν
προκύπτει ότι υπάρχουν  ώστε
ώστε  οπότε η πρώτη συνθήκη γίνεται
οπότε η πρώτη συνθήκη γίνεται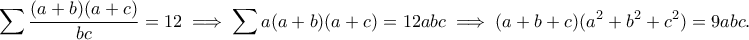
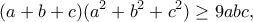 η οποία προκύπτει από τις
η οποία προκύπτει από τις ![\displaystyle{a+b+c\geq 3\sqrt[3]{abc},a^2+b^2+c^2\geq 3\sqrt[3]{abc}^2} \displaystyle{a+b+c\geq 3\sqrt[3]{abc},a^2+b^2+c^2\geq 3\sqrt[3]{abc}^2}](/forum/ext/geomar/texintegr/latexrender/pictures/33e9a5d70b0e932f3feaa6e530daa53e.png) .
. οπότε
οπότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες