Αν
 , δείξτε ότι
, δείξτε ότι  .
.Συντονιστές: achilleas, emouroukos, silouan
 , δείξτε ότι
, δείξτε ότι  .
.![3a^8 + 3b^8 + 2c^8 = a^8+a^8+a^8+b^8+b^8+b^8+c^8+c^8 \geqslant 8\sqrt[8]{(a^8)^3(b^8)^3(c^8)^2} = 8a^3b^3c^2 3a^8 + 3b^8 + 2c^8 = a^8+a^8+a^8+b^8+b^8+b^8+c^8+c^8 \geqslant 8\sqrt[8]{(a^8)^3(b^8)^3(c^8)^2} = 8a^3b^3c^2](/forum/ext/geomar/texintegr/latexrender/pictures/2d3c24ad9abe452638a22c9eb4e04c83.png)


 λαμβάνουμε το ζητούμενο.
λαμβάνουμε το ζητούμενο.Χρόνια πολλά.Ορέστης Λιγνός έγραψε: ↑Δευ Ιαν 01, 2018 4:44 pmΧρόνια Πολλά και Καλή χρονιά σε όλους!
Αν, δείξτε ότι
.

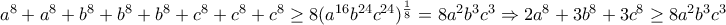
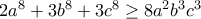
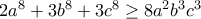

 , δηλαδή το ζητούμενο.
, δηλαδή το ζητούμενο. 
 που ισχύει από
που ισχύει από  , καθώς
, καθώς  .
.Ορέστης Λιγνός έγραψε: ↑Δευ Ιαν 01, 2018 4:44 pmΧρόνια Πολλά και Καλή χρονιά σε όλους!
Αν, δείξτε ότι
.
 Να αποδείξετε ότι:
Να αποδείξετε ότι: 
Με την υπόθεση ότιDatis-Kalali έγραψε: ↑Δευ Ιαν 01, 2018 5:35 pmΟρέστης Λιγνός έγραψε: ↑Δευ Ιαν 01, 2018 4:44 pmΧρόνια Πολλά και Καλή χρονιά σε όλους!
Αν, δείξτε ότι
.
Πιο γενικά , για κάθεΝα αποδείξετε ότι:
Υπόδειξη : Βοηθά η ανισότητα Muirhead

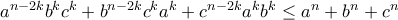

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες