 , το πολυώνυμο
, το πολυώνυμο  δεν έχει πραγματικές ρίζες πέραν των
δεν έχει πραγματικές ρίζες πέραν των  και
και 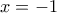 .
.Συντονιστές: achilleas, emouroukos, silouan
 , το πολυώνυμο
, το πολυώνυμο  δεν έχει πραγματικές ρίζες πέραν των
δεν έχει πραγματικές ρίζες πέραν των  και
και 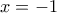 .
.Επαναφορά!gbaloglou έγραψε:Να δειχθεί ότι, για περιττό, το πολυώνυμο
δεν έχει πραγματικές ρίζες πέραν των
και
.




Γεια σου Γιώργο.gbaloglou έγραψε:Σημαδιακό το ότι η λύση εμφανίζεται, έστω και σκιαγραφημένη, περίπου ("on or about") στα γενέθλια (facebook) του Σωτήρη Λουρίδα, που είναι και ο ουσιαστικός δημιουργός του προβλήματος! (Πως και γιατί θα αποκαλυφθεί αργότερα, δίνω τώρα την ευκαιρία και για άλλες λύσεις, μία από τις οποίες θα είναι δική μου, άνευ επαγωγής...)
 αν και μόνον αν
αν και μόνον αν  . Αυτό προκύπτει άμεσα από την ισότητα
. Αυτό προκύπτει άμεσα από την ισότητα![P(x)=(x+1)[x(x-1)^{n+1}(x^{n-3}+...+x^2+1)+(x-1)^n+(x+1)^{n-1}] P(x)=(x+1)[x(x-1)^{n+1}(x^{n-3}+...+x^2+1)+(x-1)^n+(x+1)^{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/97974a7fdb8d6278bc7b81d2e7b42869.png)
 είναι θετικό για
είναι θετικό για  και αρνητικό για
και αρνητικό για  .
.  &
&  για
για  ,
,  &
&  για
για  , και
, και 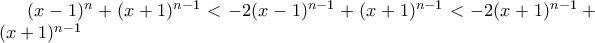
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες