 της διαμέτρου
της διαμέτρου 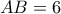 ενός ημικυκλίου , υψώνω το κάθετο τμήμα
ενός ημικυκλίου , υψώνω το κάθετο τμήμα  . Φέρω
. Φέρω την εφαπτομένη του τόξου στο σημείο
 και ονομάζω
και ονομάζω  την προβολή του
την προβολή του  , πάνω σ΄αυτήν .
, πάνω σ΄αυτήν .Υπολογίστε το μέγιστο μήκος του τμήματος
 και την
και την  , την στιγμή της μεγιστοποίησης .
, την στιγμή της μεγιστοποίησης . της διαμέτρου
της διαμέτρου 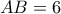 ενός ημικυκλίου , υψώνω το κάθετο τμήμα
ενός ημικυκλίου , υψώνω το κάθετο τμήμα  . Φέρω
. Φέρω  και ονομάζω
και ονομάζω  την προβολή του
την προβολή του  , πάνω σ΄αυτήν .
, πάνω σ΄αυτήν . και την
και την  , την στιγμή της μεγιστοποίησης .
, την στιγμή της μεγιστοποίησης .α) Επειδή ηKARKAR έγραψε: ↑Τετ Οκτ 06, 2021 7:30 pmΜέγιστο και εφαπτομένη.pngΣε σημείοτης διαμέτρου
ενός ημικυκλίου , υψώνω το κάθετο τμήμα
. Φέρω
την εφαπτομένη του τόξου στο σημείοκαι ονομάζω
την προβολή του
, πάνω σ΄αυτήν .
Υπολογίστε το μέγιστο μήκος του τμήματοςκαι την
, την στιγμή της μεγιστοποίησης .
 διχοτομεί την
διχοτομεί την  το τετράπλευρο
το τετράπλευρο  είναι εγγράψιμος χαρταετός και ας είναι
είναι εγγράψιμος χαρταετός και ας είναι  το κέντρο του κύκλου του .
το κέντρο του κύκλου του .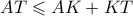 την πιο μεγάλη τιμή την παίρνει όταν τα
την πιο μεγάλη τιμή την παίρνει όταν τα  είναι συνευθειακά .
είναι συνευθειακά .
 είναι ισοσκελές τραπέζιο (
είναι ισοσκελές τραπέζιο ( )
) ,
,  ( σχήμα) έχω :
( σχήμα) έχω :  .
. 
 . .
. .  , βρίσκω ακόμα
, βρίσκω ακόμα  .
.ΕίναιKARKAR έγραψε: ↑Τετ Οκτ 06, 2021 7:30 pmΜέγιστο και εφαπτομένη.pngΣε σημείοτης διαμέτρου
ενός ημικυκλίου , υψώνω το κάθετο τμήμα
. Φέρω
την εφαπτομένη του τόξου στο σημείοκαι ονομάζω
την προβολή του
, πάνω σ΄αυτήν .
Υπολογίστε το μέγιστο μήκος του τμήματοςκαι την
, την στιγμή της μεγιστοποίησης .
 ,
,
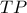 Από το νόμο των συνημιτόνων στο τρίγωνο
Από το νόμο των συνημιτόνων στο τρίγωνο 

 Αρα
Αρα 

 προκύπτει όταν
προκύπτει όταν  .
. η προβολή του
η προβολή του  στην
στην  .
.  η διάμεσός του
η διάμεσός του  άρα
άρα 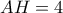 .
. κι έτσι :
κι έτσι :  έχω:
έχω:  και
και 

ΈστωKARKAR έγραψε: ↑Τετ Οκτ 06, 2021 7:30 pmΜέγιστο και εφαπτομένη.pngΣε σημείοτης διαμέτρου
ενός ημικυκλίου , υψώνω το κάθετο τμήμα
. Φέρω
την εφαπτομένη του τόξου στο σημείοκαι ονομάζω
την προβολή του
, πάνω σ΄αυτήν .
Υπολογίστε το μέγιστο μήκος του τμήματοςκαι την
, την στιγμή της μεγιστοποίησης .
 το κέντρο του ημικυκλίου και
το κέντρο του ημικυκλίου και  Τότε
Τότε  Από τα όμοια τρίγωνα
Από τα όμοια τρίγωνα  είναι
είναι 

 έχω
έχω 
 δίνει
δίνει 


 .
. , οπότε
, οπότε  .
. στο
στο  έχει εξίσωση
έχει εξίσωση  .
. έχει εξίσωση
έχει εξίσωση  ,
, 
 , που έχει μέγιστο για
, που έχει μέγιστο για  , με τιμή
, με τιμή  .
. , είναι
, είναι  ,
,  , οπότε
, οπότε 
 και
και  Έστω
Έστω  το μέσο του
το μέσο του  Με τους τύπους των διαμέσων εύκολα βρίσκω ότι
Με τους τύπους των διαμέσων εύκολα βρίσκω ότι  Άρα
Άρα  είναι ορθογώνιο και
είναι ορθογώνιο και  είναι το βαρύκεντρο του
είναι το βαρύκεντρο του  οπότε
οπότε 
 . Παρακαλώ για την μεταφορά ...
. Παρακαλώ για την μεταφορά ...Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες