 Τα εμβαδά των δύο τριγώνων φαίνονται στο σχήμα . Υπολογίστε το εμβαδόν του
Τα εμβαδά των δύο τριγώνων φαίνονται στο σχήμα . Υπολογίστε το εμβαδόν του 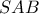 .
.Συντονιστές: silouan, Doloros, george visvikis
 Τα εμβαδά των δύο τριγώνων φαίνονται στο σχήμα . Υπολογίστε το εμβαδόν του
Τα εμβαδά των δύο τριγώνων φαίνονται στο σχήμα . Υπολογίστε το εμβαδόν του 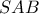 .
.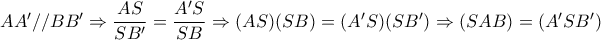 (αφού και οι περιεχόμενες γωνίες ανάμεσα στις πλευρές είναι ίσες)
(αφού και οι περιεχόμενες γωνίες ανάμεσα στις πλευρές είναι ίσες)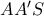 και
και  είναι όμοια με λόγο ομοιότητας
είναι όμοια με λόγο ομοιότητας 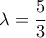 αρα
αρα 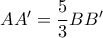

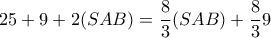 και τελικά
και τελικά 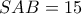
 η απόσταση του
η απόσταση του  από την
από την 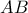 .
. . Έστω
. Έστω 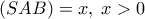 .
.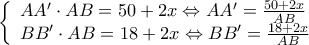
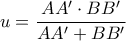 άρα
άρα 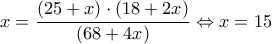
 , που διατυπώνεται ως εξής: "Η απόστασή του
, που διατυπώνεται ως εξής: "Η απόστασή του  από την
από την  είναι ανεξάρτητη του μήκους της
είναι ανεξάρτητη του μήκους της  ". Παρατηρήστε ότι είναι ο τύπος του αρμονικού μέσου των δύο άλλων καθέτων. Σε εύλογο χρόνο θα επανέλθω με περισσότερα στοιχεία.
". Παρατηρήστε ότι είναι ο τύπος του αρμονικού μέσου των δύο άλλων καθέτων. Σε εύλογο χρόνο θα επανέλθω με περισσότερα στοιχεία.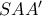 ,
,  είναι ίσος με
είναι ίσος με 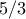 και θα είναι
και θα είναι
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 20 επισκέπτες