 , μήκους
, μήκους  , ολισθαίνει πάνω στην υποτείνουσα
, ολισθαίνει πάνω στην υποτείνουσα  , ορθογωνίου τριγώνου
, ορθογωνίου τριγώνου  , με :
, με :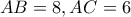 . Ονομάζουμε
. Ονομάζουμε  , τις προβολές των
, τις προβολές των  στην
στην  και
και  τις
τις προβολές των
 στην
στην  . Υπολογίστε το μέγιστο εμβαδόν του πολυγώνου
. Υπολογίστε το μέγιστο εμβαδόν του πολυγώνου  .
.Συντονιστές: silouan, Doloros, george visvikis
 , μήκους
, μήκους  , ολισθαίνει πάνω στην υποτείνουσα
, ολισθαίνει πάνω στην υποτείνουσα  , ορθογωνίου τριγώνου
, ορθογωνίου τριγώνου  , με :
, με :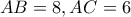 . Ονομάζουμε
. Ονομάζουμε  , τις προβολές των
, τις προβολές των  στην
στην  και
και  τις
τις  στην
στην  . Υπολογίστε το μέγιστο εμβαδόν του πολυγώνου
. Υπολογίστε το μέγιστο εμβαδόν του πολυγώνου  .
.Θέτω
 Το
Το  είναι όμοιο με το
είναι όμοιο με το  με λόγο ομοιότητας
με λόγο ομοιότητας  άρα
άρα  και
και  Εξάλλου και τα τρίγωνα
Εξάλλου και τα τρίγωνα  είναι
είναι  οπότε
οπότε 

 To ζητούμενο εμβαδόν μεγιστοποιείται όταν ελαχιστοποιηθεί το άθροισμα
To ζητούμενο εμβαδόν μεγιστοποιείται όταν ελαχιστοποιηθεί το άθροισμα

 όταν
όταν 
 που αβίαστα με τους συμβολισμούς του
που αβίαστα με τους συμβολισμούς του  αλλά
αλλά  άρα αρκεί
άρα αρκεί  .
. βρίσκουμε ότι
βρίσκουμε ότι  .
. το σημείο τομής των ευθυγράμμων τμημάτων
το σημείο τομής των ευθυγράμμων τμημάτων  και
και  . To τρίγωνο
. To τρίγωνο  είναι όμοιο με το
είναι όμοιο με το  οπότε
οπότε  και τελικά
και τελικά  και
και 
 . Το
. Το  βρίσκεται στο διάστημα [0,5.6].
βρίσκεται στο διάστημα [0,5.6]. και
και  είναι όμοια άρα
είναι όμοια άρα  ή
ή  δηλαδή
δηλαδή  και
και 

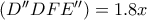



 .
.  με
με  για
για  και
και  άρα στο
άρα στο  έχουμε τοπικό μέγιστο και το συνολικό εμβαδόν είναι
έχουμε τοπικό μέγιστο και το συνολικό εμβαδόν είναι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες