Σελίδα 1 από 1
Ίσες γωνίες 41
Δημοσιεύτηκε: Δευ Φεβ 11, 2019 10:02 pm
από KARKAR

- Ίσες γωνίες.png (13.69 KiB) Προβλήθηκε 870 φορές
Το σημείο

είναι το μέσο της χορδής

και το

τυχαίο σημείο της .
Η κάθετη της χορδής στο

τέμνει τον κύκλο στο

. Έστω

σημείο
στην προέκταση της

, ώστε :

και ας ονομάσουμε

,
την τομή της

με τον κύκλο . Δείξτε ότι
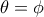
.
Re: Ίσες γωνίες 41
Δημοσιεύτηκε: Δευ Φεβ 11, 2019 11:14 pm
από Doloros
Ας είναι

το κέντρο του κύκλου και

το άλλο σημείο τομής της

με το κύκλο. Φέρνω την ευθεία
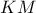
που προφανώς είναι άξονας συμμετρίας του κύκλου .
Αφού στο τρίγωνο

η

είναι μεσοκάθετος , θα είναι ισοσκελές και
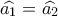

- Ισες γωνίες 41.png (27.05 KiB) Προβλήθηκε 843 φορές
Τα τρίγωνα
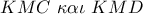
είναι αμβλυγώνια κι έχουν ακόμα
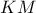
κοινή και

άρα (έμμεσο κριτήριο) είναι ίσα οπότε θα έχουν

.
Η ευθεία

θα είναι έτσι κάθετη στη

και άρα

,
δηλαδή το τετράπλευρο
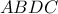
είναι ισοσκελές τραπέζιο οπότε

ως εγγεγραμμένες του ίδιου κύκλου σε ίσα τόξα.
Re: Ίσες γωνίες 41
Δημοσιεύτηκε: Δευ Φεβ 11, 2019 11:25 pm
από Xriiiiistos

τέμνει τον κύκλο για δεύτερη φορά στο

. Αφού

μεσοκάθετη της

έχουμε
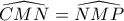

Για να είναι ίσες οι γωνίες που ζητάμε αρκεί να δείξουμε πως τα τρίγωνο

είναι όμοια δηλαδή
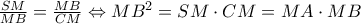

όμως από το εγγράψιμο

έχουμε

οπότε αρκεί να δείξουμε
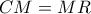

σημείο του τόξου

ώστε
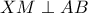
έχουμε

όμως αφού

είναι το μέσο της

τότε το

περνάει και από το

ΠΟΥ είναι το κέντρο του κύκλου
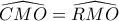
τότε to

ανήκει στην μεσοκάθετο του

οπότε

άρα


και αφού

έχουμε

Re: Ίσες γωνίες 41
Δημοσιεύτηκε: Δευ Φεβ 11, 2019 11:32 pm
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 είναι το μέσο της χορδής
είναι το μέσο της χορδής  και το
και το  τυχαίο σημείο της .
τυχαίο σημείο της . τέμνει τον κύκλο στο
τέμνει τον κύκλο στο  . Έστω
. Έστω  σημείο
σημείο , ώστε :
, ώστε :  και ας ονομάσουμε
και ας ονομάσουμε  ,
, με τον κύκλο . Δείξτε ότι
με τον κύκλο . Δείξτε ότι 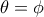 .
. είναι το μέσο της χορδής
είναι το μέσο της χορδής  και το
και το  τυχαίο σημείο της .
τυχαίο σημείο της . τέμνει τον κύκλο στο
τέμνει τον κύκλο στο  . Έστω
. Έστω  σημείο
σημείο , ώστε :
, ώστε :  και ας ονομάσουμε
και ας ονομάσουμε  ,
, με τον κύκλο . Δείξτε ότι
με τον κύκλο . Δείξτε ότι 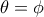 .
. το κέντρο του κύκλου και
το κέντρο του κύκλου και  το άλλο σημείο τομής της
το άλλο σημείο τομής της 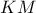 που προφανώς είναι άξονας συμμετρίας του κύκλου .
που προφανώς είναι άξονας συμμετρίας του κύκλου . η
η  είναι μεσοκάθετος , θα είναι ισοσκελές και
είναι μεσοκάθετος , θα είναι ισοσκελές και 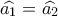
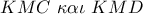 είναι αμβλυγώνια κι έχουν ακόμα
είναι αμβλυγώνια κι έχουν ακόμα  άρα (έμμεσο κριτήριο) είναι ίσα οπότε θα έχουν
άρα (έμμεσο κριτήριο) είναι ίσα οπότε θα έχουν  .
. θα είναι έτσι κάθετη στη
θα είναι έτσι κάθετη στη  και άρα
και άρα  ,
, 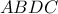 είναι ισοσκελές τραπέζιο οπότε
είναι ισοσκελές τραπέζιο οπότε  ως εγγεγραμμένες του ίδιου κύκλου σε ίσα τόξα.
ως εγγεγραμμένες του ίδιου κύκλου σε ίσα τόξα. . Αφού
. Αφού  μεσοκάθετη της
μεσοκάθετη της  έχουμε
έχουμε 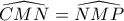
 Για να είναι ίσες οι γωνίες που ζητάμε αρκεί να δείξουμε πως τα τρίγωνο
Για να είναι ίσες οι γωνίες που ζητάμε αρκεί να δείξουμε πως τα τρίγωνο  είναι όμοια δηλαδή
είναι όμοια δηλαδή 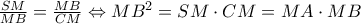
 όμως από το εγγράψιμο
όμως από το εγγράψιμο  έχουμε
έχουμε  οπότε αρκεί να δείξουμε
οπότε αρκεί να δείξουμε 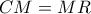
 σημείο του τόξου
σημείο του τόξου  ώστε
ώστε 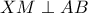 έχουμε
έχουμε  όμως αφού
όμως αφού  περνάει και από το
περνάει και από το  ΠΟΥ είναι το κέντρο του κύκλου
ΠΟΥ είναι το κέντρο του κύκλου 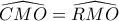 τότε to
τότε to  ανήκει στην μεσοκάθετο του
ανήκει στην μεσοκάθετο του  οπότε
οπότε  άρα
άρα 
 και αφού
και αφού 

 (κάθετες στην
(κάθετες στην 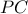 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο 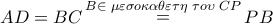 και με
και με  παραλληλόγραμμο (δύο απέναντι πλευρές ίσες και παράλληλες) άρα οι διαγώνιές του διχοτομούνται, δηλαδή η
παραλληλόγραμμο (δύο απέναντι πλευρές ίσες και παράλληλες) άρα οι διαγώνιές του διχοτομούνται, δηλαδή η 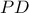 διέρχεται από το μέσο
διέρχεται από το μέσο  είναι συνευθειακά.
είναι συνευθειακά.  (εγγεγραμμένες σε ίσα τόξα (από τις παράλληλες χορδές) του ίδιου κύκλου) και το ζητούμενο έχει αποδειχθεί.
(εγγεγραμμένες σε ίσα τόξα (από τις παράλληλες χορδές) του ίδιου κύκλου) και το ζητούμενο έχει αποδειχθεί.