 είναι το έγκεντρο του ορθογωνίου τριγώνου
είναι το έγκεντρο του ορθογωνίου τριγώνου  . Ο κύκλος
. Ο κύκλος 
τέμνει την υποτείνουσα
 στο
στο  (πλησίον του
(πλησίον του  ) και την πλευρά
) και την πλευρά  στο
στο  .
.α) Δείξτε ότι
 ... β) Βρείτε την
... β) Βρείτε την  αν το
αν το  είναι το μέσο της
είναι το μέσο της  .
.Συντονιστές: silouan, Doloros, george visvikis
 είναι το έγκεντρο του ορθογωνίου τριγώνου
είναι το έγκεντρο του ορθογωνίου τριγώνου  . Ο κύκλος
. Ο κύκλος 
 στο
στο  (πλησίον του
(πλησίον του  ) και την πλευρά
) και την πλευρά  στο
στο  .
. ... β) Βρείτε την
... β) Βρείτε την  αν το
αν το  είναι το μέσο της
είναι το μέσο της  .
.α) Τα αμβλυγώνια τρίγωνα
 είναι ίσα, άρα
είναι ίσα, άρα 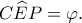 Αλλά,
Αλλά, 

 και αν
και αν  τότε
τότε 
 Άρα,
Άρα, 

 ισοσκελές τραπέζιο ,άρα
ισοσκελές τραπέζιο ,άρα 
 διάμετρος
διάμετρος .Άρα,
.Άρα, 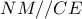
 είναι ισοσκελές ορθογώνιο και με
είναι ισοσκελές ορθογώνιο και με  μέσο της
μέσο της  είναι
είναι 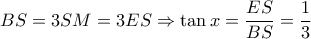
 παίρνουμε
παίρνουμε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες