 , φέρουμε τη διχοτόμο
, φέρουμε τη διχοτόμο  , καθώς και τμήματα :
, καθώς και τμήματα :  ,
,  . Ενδιαφερόμαστε για τον λόγο των διαγωνίων
. Ενδιαφερόμαστε για τον λόγο των διαγωνίων 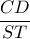
του σχηματιζόμενου ρόμβου - γιατί είναι ρόμβος ; -
 .
.Ποιος είναι ο λόγος
 , αν :
, αν : 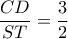 ; Ποιος είναι ο λόγος
; Ποιος είναι ο λόγος 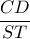 , αν :
, αν :  ;
;Συντονιστές: silouan, Doloros, george visvikis
 , φέρουμε τη διχοτόμο
, φέρουμε τη διχοτόμο  , καθώς και τμήματα :
, καθώς και τμήματα :  ,
,  . Ενδιαφερόμαστε για τον λόγο των διαγωνίων
. Ενδιαφερόμαστε για τον λόγο των διαγωνίων 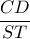
 .
. , αν :
, αν : 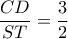 ; Ποιος είναι ο λόγος
; Ποιος είναι ο λόγος 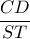 , αν :
, αν :  ;
;Μία εκτός φακέλου. Λόγω της διχοτόμου και των παραλληλιών προκύπτει ότι το παραλληλόγραμμο
 είναι ρόμβος.
είναι ρόμβος.

 ( υπόθεση) και
( υπόθεση) και 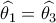 (
(  ) θα είναι
) θα είναι 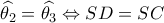
 είναι ρόμβος. Έστω
είναι ρόμβος. Έστω  το σημείο τομής των
το σημείο τομής των  .
.  παράλληλη στην
παράλληλη στην  που τέμνει την ευθεία
που τέμνει την ευθεία  στο
στο  .
. . Αφού τώρα
. Αφού τώρα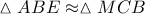 θα είναι :
θα είναι : 
 η προηγούμενη γίνεται :
η προηγούμενη γίνεται :  έτσι η εξίσωση αυτή δίδει :
έτσι η εξίσωση αυτή δίδει : 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες