 έχουν άθροισμα
έχουν άθροισμα 
Να βρείτε τη μέγιστη και την ελάχιστη τιμή της παράστασης

 έχουν άθροισμα
έχουν άθροισμα 

Αποδυκνύεται ότι
 , με ισότητες στα
, με ισότητες στα  και, αντίστοιχα,
και, αντίστοιχα,  .
. 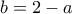 . Tότε η μεν αριστερή γράφεται
. Tότε η μεν αριστερή γράφεται  , ισοδύναμα
, ισοδύναμα  , που ισχύει. Η δε δεξιά γράφεται
, που ισχύει. Η δε δεξιά γράφεται  , ισοδύναμα
, ισοδύναμα  , που ισχύει αφού
, που ισχύει αφού  .
. και παρατηρούμε ότι
και παρατηρούμε ότι 

 και
και  .
.  , οπότε
, οπότε  , και αφού
, και αφού  , θα είναι
, θα είναι
 .
.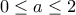 , οπότε, έχουμε τις ανισώσεις
, οπότε, έχουμε τις ανισώσεις

 και
και  αντίστοιχα.
αντίστοιχα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες