
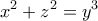

Να εξηγήσω:

 , από την πρώτη σχέση
, από την πρώτη σχέση 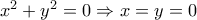


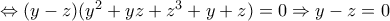 , καθώς
, καθώς 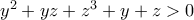
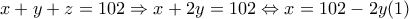
 και την πρώτη σχέση:
και την πρώτη σχέση: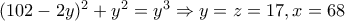
Σύμφωνα με τον κανονισμό του mathematica,
2. Οι απαντήσεις πρέπει να είναι κατά τα δυνατόν πλήρεις να αποφεύγονται οι υποδείξεις και η παράθεση μόνο του αποτελέσματος.
Η λύση είναι κατά βάση σωστή, αλλά είναι
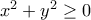 , και όχι
, και όχι 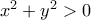 .
. 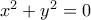 αν και μόνο αν
αν και μόνο αν  , που αντιβαίνει στην τελευταία δοθείσα σχέση.
, που αντιβαίνει στην τελευταία δοθείσα σχέση.Απροσεξία. Το διορθώνω.achilleas έγραψε: ↑Τρί Νοέμ 09, 2021 11:32 pmΣύμφωνα με τον κανονισμό του mathematica,
2. Οι απαντήσεις πρέπει να είναι κατά τα δυνατόν πλήρεις να αποφεύγονται οι υποδείξεις και η παράθεση μόνο του αποτελέσματος.Η λύση είναι κατά βάση σωστή, αλλά είναι, και όχι
.
Φυσικά συμπληρώνεται εύκολα με την παρατήρηση ότιαν και μόνο αν
, που αντιβαίνει στην τελευταία δοθείσα σχέση.
Φιλικά,
Αχιλλέας
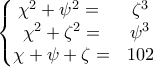
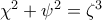


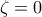 τότε
τότε  Άτοπο αφού
Άτοπο αφού 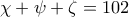
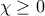 και
και 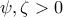
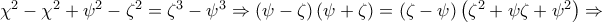


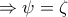 ή
ή 
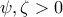 κι έτσι έχω
κι έτσι έχω 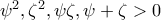 (δηλαδή είναι θετικοί όλοι οι όροι)
(δηλαδή είναι θετικοί όλοι οι όροι)

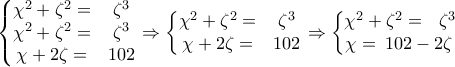


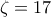
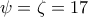 και
και 

Παρόλα αυτά κανένας από εμάς δεν απέδειξε για ποιο λόγο ζ=17 ή αντίστοιχα για ποιο λόγο ψ=17 (μιας και ζ=ψ).achilleas έγραψε: ↑Τρί Νοέμ 09, 2021 11:32 pmΣύμφωνα με τον κανονισμό του mathematica,
2. Οι απαντήσεις πρέπει να είναι κατά τα δυνατόν πλήρεις να αποφεύγονται οι υποδείξεις και η παράθεση μόνο του αποτελέσματος.Η λύση είναι κατά βάση σωστή, αλλά είναι, και όχι
.
Φυσικά συμπληρώνεται εύκολα με την παρατήρηση ότιαν και μόνο αν
, που αντιβαίνει στην τελευταία δοθείσα σχέση.
Φιλικά,
Αχιλλέας
 ) την έλυσα με υπολογιστή τσέπης. Αν μπορεί κάποιος να γράψει την απόδειξη.
) την έλυσα με υπολογιστή τσέπης. Αν μπορεί κάποιος να γράψει την απόδειξη.Κατά την διαίρεσή του με το πολυώνυμοNickSpanoudis έγραψε: ↑Σάβ Νοέμ 13, 2021 2:25 pmΠαρόλα αυτά κανένας από εμάς δεν απέδειξε για ποιο λόγο ζ=17 ή αντίστοιχα για ποιο λόγο ψ=17 (μιας και ζ=ψ).achilleas έγραψε: ↑Τρί Νοέμ 09, 2021 11:32 pmΣύμφωνα με τον κανονισμό του mathematica,
2. Οι απαντήσεις πρέπει να είναι κατά τα δυνατόν πλήρεις να αποφεύγονται οι υποδείξεις και η παράθεση μόνο του αποτελέσματος.Η λύση είναι κατά βάση σωστή, αλλά είναι, και όχι
.
Φυσικά συμπληρώνεται εύκολα με την παρατήρηση ότιαν και μόνο αν
, που αντιβαίνει στην τελευταία δοθείσα σχέση.
Φιλικά,
Αχιλλέας
Δηλαδή, εγώ προσωπικά την τριτοβάθμια εξίσωση () την έλυσα με υπολογιστή τσέπης. Αν μπορεί κάποιος να γράψει την απόδειξη.
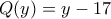 , το πολυώνυμο
, το πολυώνυμο 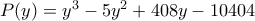 μας δίνει πηλίκο
μας δίνει πηλίκο 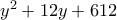 και υπόλοιπο
και υπόλοιπο  (Με σχήμα Horner). Άρα παραγοντοποιείται και δεχόμαστε την
(Με σχήμα Horner). Άρα παραγοντοποιείται και δεχόμαστε την 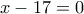 για μόνη ακέραιη λύση της εξίσωσης.
για μόνη ακέραιη λύση της εξίσωσης.Μπορούμε και χωρίς το σχήμα του Horner, να βρούμε την λύση , (με λίγο κόπο βέβαια)NickSpanoudis έγραψε: ↑Σάβ Νοέμ 13, 2021 2:25 pm
Παρόλα αυτά κανένας από εμάς δεν απέδειξε για ποιο λόγο ζ=17 ή αντίστοιχα για ποιο λόγο ψ=17 (μιας και ζ=ψ).
Δηλαδή, εγώ προσωπικά την τριτοβάθμια εξίσωση () την έλυσα με υπολογιστή τσέπης. Αν μπορεί κάποιος να γράψει την απόδειξη.
 , τότε η πρώτη των εξισώσεων γράφεται:
, τότε η πρώτη των εξισώσεων γράφεται: 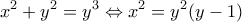 .
. όπου
όπου 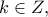 . Άρα
. Άρα  .
.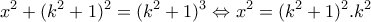
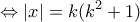 , και
, και 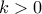
 .
.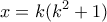 . Αφού όμως
. Αφού όμως  θα έχουμε:
θα έχουμε: 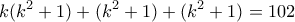 και άρα:
και άρα: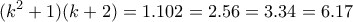 . (ΣΧΕΣΗ 1)
. (ΣΧΕΣΗ 1) , έχουμε
, έχουμε 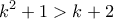 , ενώ αν
, ενώ αν 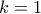 , θα είναι
, θα είναι 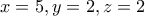 , που είναι αδύνατον
, που είναι αδύνατον . Άρα από την ΣΧΕΣΗ 1, παίρνουμε
. Άρα από την ΣΧΕΣΗ 1, παίρνουμε 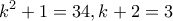 , ή
, ή  , από όπου
, από όπου . Τότε
. Τότε  .
.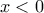 .
. , και αφού
, και αφού  , βρίσκουμε
, βρίσκουμε  και από εδώ,
και από εδώ,  ,
,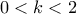 . Άρα
. Άρα 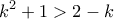 .
.  , και δεδομένου ότι ο
, και δεδομένου ότι ο  είναι ακέραιος, εύκολα βλέπουμε
είναι ακέραιος, εύκολα βλέπουμε  .
. 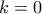 και άρα
και άρα 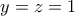 , είναι αδύνατον, αφού
, είναι αδύνατον, αφού 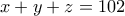
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 18 επισκέπτες