Νόμος της τετραγωνικής αντιστροφής

Συντονιστής: polysot

Απάντηση
Άβαταρ μέλους
Demetres
Γενικός Συντονιστής
Δημοσιεύσεις: 8989
Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
Τοποθεσία: Λεμεσός/Πύλα
Επικοινωνία:
Επικοινωνία Demetres

Νόμος της τετραγωνικής αντιστροφής

#1

Μη αναγνωσμένη δημοσίευση από Demetres » Σάβ Δεκ 24, 2016 4:21 pm

Προαπαιτούμενα: Πρώτοι αριθμοί, Αριθμητική υπολοίπων (modular arithmetic)
Άλλες επιθυμητές γνώσεις: Μικρό θεώρημα Fermat, Θεώρημα Wilson
Επίπεδο: Απολύτως απαραίτητο σε όσους λαμβάνουν μέρους σε διεθνείς διαγωνισμούς. Επιθυμητό σε όσους λαμβάνουν μέρος στον Αρχιμήδη των μεγάλων και πάνω. Επιθυμητό για όσους juniors θα λάβουν μέρος σε διεθνείς διαγωνισμούς.

Εδώ θα μας απασχολήσει αν υπάρχουν λύσεις ή όχι σε εξισώσεις της μορφής x^2 = \equiv a \bmod p όπου ο p είναι πρώτος. Για p=2 η εξίσωση έχει πάντα λύση οπότε στα περισσότερα που θα ακολουθήσουν ο p θα είναι περιττός πρώτος.

Ορισμός: Έστω ένας πρώτος p και έστω ακέραιος a ο οποίος δεν είναι πολλαπλάσιο του p. Αν η εξίσωση x^2 \equiv a \bmod p έχει λύση, τότε ονομάζουμε τον a τετραγωνικό υπόλοιπο ή τετραγωνικό κατάλοιπο \mod p. Αλλιώς ονομάζεται μη τετραγωνικό υπόλοιπο \mod p.

Παραδείγματα:

(α) Αν x \equiv 0 \bmod 3, τότε x^2 \equiv 0 \bmod 3. Αν x \equiv 1 \bmod 3, τότε x^2 \equiv 1 \bmod 3. Αν x \equiv 2 \bmod 3, τότε x^2 \equiv 4 \equiv 1 \bmod 3. Οπότε

- Τα τετραγωνικά υπόλοιπα \mod 3 είναι όλοι οι αριθμοί της μορφής 1 \bmod 3.
- Τα μη τετραγωνικά υπόλοιπα \mod 3 είναι όλοι οι αριθμοί της μορφής 2 \bmod 3.

(β) Δουλεύοντας με παρόμοιο τρόπο, τα τετραγωνικά υπόλοιπα \bmod 5 είναι όλοι οι αριθμοί της μορφής 1,4 \bmod 5. Τα μη τετραγωνικά υπόλοιπα είναι όλοι οι αριθμοί της μορφής 2,3 \bmod 5.

(γ) Τα τετραγωνικά υπόλοιπα \bmod 7 είναι όλοι οι αριθμοί της μορφής 1,2,4 \bmod 7. Τα μη τετραγωνικά υπόλοιπα είναι όλοι οι αριθμοί της μορφής 35,6 \bmod 7.

Ορισμός: Έστω p περιττός πρώτος. Ορίζουμε το σύμβολο Legendre ως εξής:

\displaystyle{ \left( \frac{a}{p} \right) = \begin{cases} 0 & \text{\gr αν } p|a \\ 1 & \text{\gr αν υπάρχει } x \not \equiv 0 \bmod p \text{ \gr με } x^2 \equiv a \bmod p \\ -1 & \text{\gr αν δεν υπάρχει } x \text{ \gr με } x^2 \equiv a \bmod p\end{cases}}

Παραδείγματα:

(α) \displaystyle{\left( \frac{21}{7} \right) = 0 } αφού 7|21.

(β) \displaystyle{\left( \frac{23}{7} \right) = 1 } αφού 7 \nmid 23 και επιπλέον 3^2 = 9 \equiv 23 \bmod 7. Αλλιώς: Είναι 23 \equiv 2 \bmod 7 και γνωρίζουμε από προηγούμενο παράδειγμα ότι το 2 είναι τετραγωνικό υπόλοιπο \mod 7.

(γ) \displaystyle{\left( \frac{31}{7} \right) = -1 } αφού 31 \equiv 3 \bmod 7 και γνωρίζουμε ότι το 3 είναι μη τετραγωνικό υπόλοιπο \bmod 7.

Άμεσα από τον ορισμό προκύπτουν οι εξής προφανείς ιδιότητες:

Ιδιότητα 1: Έστω p περιττός πρώτος και a,b με a \equiv b \bmod p. Τότε \displaystyle{\left( \frac{a}{p} \right) = \left( \frac{b}{p} \right) .}

Ιδιότητα 2: Έστω p περιττός πρώτος. Τότε

\displaystyle{\left( \frac{a^2}{p} \right) = \begin{cases} 0 & \text{\gr αν } p|a \\ 1 & \text{\gr αν } p \nmid a.\end{cases}}

Λόγω της Ιδιότητας 1 συνηθίζουμε να λέμε π.χ. ότι τα τετραγωνικά υπόλοιπα \bmod 7 είναι τα 1,2,4 αντί να λέμε ότι είναι όλοι οι αριθμοί της μορφής 1,2,4 \bmod 7.

Πρόταση: Αν p περιττός πρώτος, τότε υπάρχουν ακριβώς (p-1)/2 τετραγωνικά υπόλοιπα \bmod p και ακριβώς (p-1)/2 μη τετραγωνικά υπόλοιπα \bmod p.

Παραδείγματα: Έχουμε ήδη δει ότι η πρόταση ισχύει για p=5 και p=7.

Απόδειξη:
Παρατηρούμε ότι x^2 \equiv y^2 \bmod p αν και μόνο αν x \equiv y \bmod p ή x \equiv -y \bmod p. Άρα τα τετραγωνικά υπόλοιπα \bmod p είναι τα 1^2 , 2^2, \ldots, [(p-1)/2]^2.

Δηλαδή έχουμε (p-1)/2 τετραγωνικά υπόλοιπα \bmod p όλα τα υπόλοιπα υπόλοιπα \bmod p δηλαδή άλλα (p-1)/2 είναι μη τετραγωνικά υπόλοιπα.
Ένας τρόπος για να υπολογίσουμε το σύμβολο Legendre είναι ο εξής:

Κριτήριο Euler: Έστω p περιττός πρώτος και a σχετικά πρώτος ως προς τον p. Τότε

\displaystyle{ \left( \frac{a}{p} \right) \equiv a^{(p-1)/2} \bmod p }

Παραδείγματα:

(α) \displaystyle{ \left(\frac{23}{7} \right) = \left(\frac{2}{7} \right) \equiv 2^{(7-1)/2} \equiv 8 \equiv 1 \bmod 7}

(β) \displaystyle{ \left(\frac{31}{7} \right) = \left(\frac{3}{7} \right) \equiv 3^{(7-1)/2} \equiv 27 \equiv -1 \bmod 7}

Απόδειξη:
Από το μικρό θεώρημα του Fermat, έχουμε a^{p-1} \equiv 1 \bmod p. Ισοδύναμα, \displaystyle{(a^{(p-1)/2}-1)(a^{(p-1)/2}+1) \equiv 0 \bmod p} Επειδή ο p είναι πρώτος παίρνουμε a^{(p-1)/2} \equiv -1 \bmod p ή a^{(p-1)/2} \equiv 1 \bmod p.

Αν ο a είναι τετραγωνικό υπόλοιπο \mod p τότε υπάρχει x ώστε x^2 \equiv a \bmod p. Επειδή (a,p)=1 είναι και (x,p)=1. Άρα από το μικρό θεώρημα του Fermat παίρνουμε
\displaystyle{ a^{(p-1)/2} \equiv (x^2)^{(p-1)/2} \equiv x^{p-1} \equiv 1 \bmod p}

Αν ο a δεν είναι τετραγωνικό υπόλοιπο \mod p, θα δείξουμε ότι a^{(p-1)/2} \not \equiv 1 \bmod p και άρα αναγκαστικά είναι a^{(p-1)/2} \equiv -1 \bmod p. (Οπότε η απόδειξη θα ολοκληρωθεί.)

Κοιτάζουμε την εξίσωση \displaystyle{ x^{(p-1)/2} \equiv 1 \bmod p} Γνωρίζουμε ότι υπάρχουν (p-1)/2 τετραγωνικά υπόλοιπα \bmod p τα οποία όλα ικανοποιούν αυτήν εξίσωση. Επειδή οι αριθμοί \bmod p είναι σώμα η εξίσωση δεν μπορεί να έχει περισσότερες από (p-1)/2 λύσεις. Άρα οι μόνες λύσεις της είναι τα τετραγωνικά υπόλοιπα \bmod p. Οπότε όντως τα μη τετραγωνικά υπόλοιπα δεν ικανοποιούν αυτήν την εξίσωση.
Η χρήση του κριτηρίου του Euler είναι εν γένει δύσκολη. Θα δούμε αργότερα ένα πολύ πιο εύκολο τρόπο υπολογισμού του συμβόλου Legendre. Αυτός ο τρόπος βασίζεται σε κάποιες επιπλέον ιδιότητες του συμβόλου. Πριν να τις αποδείξουμε ας δούμε ακόμη ένα θεωρητικό κυρίως αποτέλεσμα.

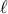Λήμμα Gauss: Έστω p περιττός πρώτος και a σχετικά πρώτος ως προς τον p. Κοιτάμε τα υπόλοιπα που αφήνουν οι \displaystyle{a,2a,\ldots,\left(\frac{p-1}{2}\right)a} όταν διαιρεθούν με τον p. Έστω ότι ακριβώς \ell από αυτά είναι μεγαλύτερα του (p-1)/2. Τότε \displaystyle{ \left( \frac{a}{p} \right) = (-1)^{\ell}.}

Παράδειγμα:

Για p=13 και a=5, κοιτάμε τα 5,10,15,20,25,30 τα οποία αφήνουν υπόλοιπα 5,10,2,7,12,4. Ακριβώς 3 είναι μεγαλύτερα του 6 οπότε \displaystyle{ \left(\frac{5}{13} \right) = -1}

Απόδειξη:
Θα υπολογίσουμε το γινόμενο \displaystyle{ \prod_{k=1}^{(p-1)/2} (ka)} με δύο διαφορετικούς τρόπους. Καταρχάς το γινόμενο σίγουρα ισούται με \displaystyle{ N! a^{(p-1)/2}} όπου N = (p-1)/2.

Διαφορετικά, αν m το υπόλοιπο του ka όταν διαιρεθεί με τον p, ορίζουμε f(k) = m αν m \leqslant (p-1)/2 και f(k) = m-p αν m > (p-1)/2. Παρατηρούμε ότι για 1 \leqslant k,r\leqslant (p-1)/2 με k \neq \ell έχουμε |f(k)| \neq |f(r)|. Πράγματι αν f(k) = f(r), τότε \displaystyle{ ka \equiv ra \bmod p} οπότε k = r ενώ αν f(k) = -f(r) τότε \displaystyle{ (k + r)a \equiv 0 \bmod p} το οποίο είναι άτοπο αφού 2 \leqslant k+r\leqslant p-1. Οπότε τα |f(1)|,|f(2)|,\ldots,|f((p-1)/2)| ισούνται με 1,2,\ldots,(p-1)/2 με κάποια σειρά. Επιπλέον ακριβώς \ell από τα f(1),\ldots,f((p-1)/2) είναι αρνητικά. Άρα εν τέλει το αρχικό γινόμενο ισούται modulo p με \displaystyle{ N! (-1)^{\ell}}} όπου N = (p-1)/2.

Επομένως \displaystyle{ a^{(p-1)/2} \equiv (-1)^{\ell} \bmod p} και το αποτέλεσμα έπεται από το κριτήριο του Euler.
Οι βασικές επιπλέον ιδιότητες είναι οι εξής:

Ιδιότητα 3: \displaystyle{ \left( \frac{ab}{p} \right) = \left( \frac{a}{p} \right)\left( \frac{b}{p} \right)}
Απόδειξη: Άμεση από το κριτήριο Euler.
Ιδιότητα 4: \displaystyle{ \left( \frac{-1}{p} \right) = \begin{cases} 1 & \text{\gr αν } p \equiv 1 \bmod 4\\ -1 & \text{\gr αν } p \equiv 3 \bmod 4\end{cases}}

Απόδειξη:
Απόδειξη: Άμεση από το κριτήριο Euler.
Ιδιότητα 5: \displaystyle{ \left( \frac{2}{p} \right) = \begin{cases} 1 & \text{\gr αν } p \equiv 1,7 \bmod 8\\ -1 & \text{\gr αν } p \equiv 3,5 \bmod 8\end{cases}}

Απόδειξη:
Χρησιμοποιούμε το λήμμα του Gauss. Κοιτάμε τα 2,4,6,\ldots,p-1.

Αν p=8k+1, τότε ακριβώς 2k είναι μεγαλύτερα του (p-1)/2 = 4k. Οπότε σε αυτήν την περίπτωση έχουμε \displaystyle{\left(\frac{2}{p} \right) = 1}

Αν p=8k+3, τότε ακριβώς 2k+1 είναι μεγαλύτερα του (p-1)/2 = 4k+1. Οπότε σε αυτήν την περίπτωση έχουμε \displaystyle{\left(\frac{2}{p} \right) = -1}

Αν p=8k+5, τότε ακριβώς 2k+1 είναι μεγαλύτερα του (p-1)/2 = 4k+2. Οπότε σε αυτήν την περίπτωση έχουμε \displaystyle{\left(\frac{2}{p} \right) = -1}

Αν p=8k+7, τότε ακριβώς 2k+2 είναι μεγαλύτερα του (p-1)/2 = 4k+3. Οπότε σε αυτήν την περίπτωση έχουμε \displaystyle{\left(\frac{2}{p} \right) = -1}
Ιδιότητα 6: (Νόμος τετραγωνικής αντιστροφής) Αν p,q περιττοί πρώτοι τότε:

\displaystyle{ \left( \frac{p}{q} \right) = \begin{cases} \left( \frac{q}{p} \right) & \text{\gr αν } p \equiv 1 \bmod 4 \text{ \gr ή } q \equiv 1 \bmod 4\\ -\left( \frac{q}{p} \right) & \text{\gr αν } p \equiv q \equiv 3 \bmod 4\end{cases}}

Απόδειξη:
Προσθήκη αργότερα
Παραδείγματα:

(α) \displaystyle{ \left( \frac{2482}{2017} \right) = \left( \frac{465}{2017} \right) = \left( \frac{5}{2017} \right)\left( \frac{93}{2017} \right) = \left( \frac{2017}{5} \right)\left( \frac{2017}{93} \right) = \left( \frac{2}{5} \right)\left( \frac{64}{93} \right) = -1}
Εδώ χρησιμοποιήσαμε ότι ο 2017 είναι πρώτος. Στην πρώτη ισότητα χρησιμοποιήσαμε την Ιδιότητα 1. Στην δεύτερη την Ιδιότητα 3. Στην τρίτη τον νόμο της τετραγωνικής αντιστροφής και το γεγονός ότι 2017 \equiv 1 \bmod 4. Στην επόμενη χρησιμοποιήσαμε ξανά την ιδιότητα 1. Τέλος στην τελευταία ισότητα χρησιμοποιήσαμε την Ιδιότητα 2 καθώς και το γεγονός ότι το 2 είναι μη τετραγωνικό υπόλοιπο \bmod 5.
(β) \displaystyle{\left( \frac{2500}{2017} \right) = \left( \frac{50^2}{2017} \right) = 1}
Αν όμως δεν βλέπαμε άμεσα το πιο πάνω τότε θα κάναμε τις εξής πράξεις:

\displaystyle{ \left( \frac{2500}{2017} \right) = \left( \frac{483}{2017} \right) = \left( \frac{3}{2017} \right)\left( \frac{7}{2017}\right)\left( \frac{23}{2017} \right) = \left( \frac{2017}{3} \right)\left( \frac{2017}{7} \right)\left( \frac{2017}{23} \right) = \left( \frac{1}{3} \right)\left( \frac{1}{7} \right)\left( \frac{16}{23} \right) = 1.}
(γ)

\displaystyle{ \begin{aligned} \left( \frac{2482}{2003} \right) &= \left( \frac{479}{2003} \right) = -\left( \frac{2003}{479} \right) = -\left( \frac{87}{479} \right) = -\left( \frac{3}{479} \right)\left( \frac{29}{479} \right) = \left( \frac{479}{3}\right)\left( \frac{479}{29}\right) = \left( \frac{2}{3}\right)\left( \frac{15}{29}\right) \\ &= -\left( \frac{3}{29}\right)\left( \frac{5}{29}\right) = -\left( \frac{29}{3}\right)\left( \frac{29}{5}\right) = - \left( \frac{2}{3}\right)\left( \frac{4}{5}\right) = 1 \end{aligned}}
Εδώ χρησιμοποιήσαμε αρκετές φορές τον νόμο της τετραγωνικής αντιστροφής. Χρειάζεται προσοχή ώστε σε κάθε εφαρμογή να εργαζόμαστε με πρώτους αριθμούς και όχι σύνθετους. Επιπλέον πρέπει να ελέγχουμε αν και οι δύο πρώτοι είναι της μορφής 3 \bmod 4 ή όχι. (Στην πρώτη περίπτωση αντιστρέφουμε και αλλάζουμε το πρόσημο. Στην δεύτερη περίπτωση αντιστρέφουμε χωρίς αλλαγή προσήμου.)
Άλλα παραδείγματα
viewtopic.php?p=215199#p215199
viewtopic.php?f=63&t=44673
viewtopic.php?f=182&t=56905
viewtopic.php?f=111&t=23041
viewtopic.php?f=186&t=56881
viewtopic.php?f=182&t=56905
viewtopic.php?p=218662#p218662
viewtopic.php?p=213943#p213943
viewtopic.php?p=217809#p217809
viewtopic.php?f=111&t=38101
viewtopic.php?f=111&t=40522
Αρχιμήδης 2013-14/3
BMO 2015/4

Πρόσθεσα ήδη αρκετές λεπτομέρειες. Λείπουν ακόμη κάποια πράγματα τα οποία θα προστεθούν αργότερα. Μετά τα Χριστούγεννα αλλά ελπίζω εντός 2016.


Λέξεις Κλειδιά:
τετραγωνικό-υπόλοιπο
τετραγωνικό-κατάλοιπο
τετραγωνική-ανιστροφή
σύμβολο-Legendre
θεωρία-αριθμών
Κορυφή
Απάντηση

Επιστροφή σε “Θεωρία Αριθμών”

Μέλη σε σύνδεση

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες