Μιλώντας "προβολικά", η απόδειξη θα πρέπει να γίνει έτσι, όπως την έκανε ο min£##!
Ας την δούμε, όμως, και με τον κακώς παραμελειμένο, και κατά την γνώμη μου πολύ, Μενέλαο.
Έστω

το σημείο που τέμνονται οι

. Το κλειδί είναι το τρίγωνο

του οποίου διατέμνουσες είναι δύο από τις πλευρές και οι δύο διαγώνιοι του αρχικού τετραπλεύρου. Έτσι με διατέμουσες τις πλευρές

έχουμε:

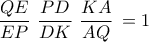
Και από εδώ θα πάρουμε:

Με αυτή την σχέση ουσιαστικά τελειώσαμε. Πραγματικά, αν δουλέψουμε, τώρα, όπως παραπάνω, με διατέμνουσες τις διαγώνιες του τετραπλεύρου, τότε ίσο με το δεύτερο μέλος της σχέσης

θα προκύψει και το

. Αυτό τελειώνει την απόδειξη του πρώτου μέρους.
Για το δεύτερο μέρος, επανερχόμαστε στην

Αν η κωνική είναι κύκλος, τότε από το θεώρημα τεμνομένων χορδών έχουμε:

Με αυτές το δεύτερο μέλος της

θα γίνει
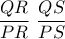
και η απόδειξη έγινε.
Αν, τέλος, η κωνική δεν είναι κύκλος, τότε θεωρούμε ένα προβολικό μετασχηματισμό που την στέλνει σε κύκλο. Ο μετασχηματισμός διατηρεί τις ισότητες των λόγων μας, και δίνει την απόδειξη.
Με επιφύλαξη για την πληκτρολόγηση. Ίσως ξέφυγε κάποιο γράμμα ...
 και ευθεία που τέμνει τις
και ευθεία που τέμνει τις 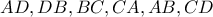 κατά σειρά στα σημεία
κατά σειρά στα σημεία  . Να αποδειχτεί ότι:
. Να αποδειχτεί ότι:
 , τότε
, τότε

 (υποθέτω-νομίζω ότι εννοείτε
(υποθέτω-νομίζω ότι εννοείτε  αντί
αντί  ),δηλαδή
),δηλαδή  .Είναι όμως
.Είναι όμως  και
και  και το ζητούμενο δείχτηκε.
και το ζητούμενο δείχτηκε. (ο διπλός λόγος δέσμης 4 σημείων και κέντρου σε κωνική είναι ανεξάρτητος του κέντρου) δηλαδή
(ο διπλός λόγος δέσμης 4 σημείων και κέντρου σε κωνική είναι ανεξάρτητος του κέντρου) δηλαδή  .Έχουμε ότι ένας προβολικός μετασχηματισμός σε μια ευθεία ορίζεται από 3 ζεύγη σημείων (δεδομένων τριών σημείων,κατασκευάζεται μονάχα ένα ώστε η τετράδα να έχει δοσμένο διπλό λόγο).Για τον προβολικό μετασχηματισμό πάνω στην l που ορίζεται από τα ζεύγη
.Έχουμε ότι ένας προβολικός μετασχηματισμός σε μια ευθεία ορίζεται από 3 ζεύγη σημείων (δεδομένων τριών σημείων,κατασκευάζεται μονάχα ένα ώστε η τετράδα να έχει δοσμένο διπλό λόγο).Για τον προβολικό μετασχηματισμό πάνω στην l που ορίζεται από τα ζεύγη  ,έστω f ,ισχύει
,έστω f ,ισχύει  για κάθε σημείο.Αυτό έπεται από την πρόταση:
για κάθε σημείο.Αυτό έπεται από την πρόταση: ,έστω
,έστω 
 ένα άλλο σημείο και
ένα άλλο σημείο και  ,θα είναι
,θα είναι  κλπ.
κλπ. στο
στο  και αντίστροφα (από
και αντίστροφα (από ) ενώ από το
) ενώ από το  στέλνει και το
στέλνει και το  στο
στο  και αντίστροφα.Τελικά δηλαδή τα ζεύγη
και αντίστροφα.Τελικά δηλαδή τα ζεύγη  είναι όλα συζηγή του ίδιου προβολικού μετασχηματισμού από το οποίο έπεται η σχέση προς απόδειξη(η ισότητα διπλών λόγων).
είναι όλα συζηγή του ίδιου προβολικού μετασχηματισμού από το οποίο έπεται η σχέση προς απόδειξη(η ισότητα διπλών λόγων). το σημείο που τέμνονται οι
το σημείο που τέμνονται οι  . Το κλειδί είναι το τρίγωνο
. Το κλειδί είναι το τρίγωνο  του οποίου διατέμνουσες είναι δύο από τις πλευρές και οι δύο διαγώνιοι του αρχικού τετραπλεύρου. Έτσι με διατέμουσες τις πλευρές
του οποίου διατέμνουσες είναι δύο από τις πλευρές και οι δύο διαγώνιοι του αρχικού τετραπλεύρου. Έτσι με διατέμουσες τις πλευρές  έχουμε:
έχουμε:
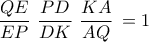

 θα προκύψει και το
θα προκύψει και το  . Αυτό τελειώνει την απόδειξη του πρώτου μέρους.
. Αυτό τελειώνει την απόδειξη του πρώτου μέρους.

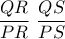 και η απόδειξη έγινε.
και η απόδειξη έγινε.