

Συντονιστής: polysot


 και για το δεύτερο το γινόμενο
και για το δεύτερο το γινόμενο 
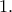 Με πρόσθεση κατά μέλη:
Με πρόσθεση κατά μέλη:  Στη συνέχεια αφαιρώντας από αυτήν τις εξισώσεις του
Στη συνέχεια αφαιρώντας από αυτήν τις εξισώσεις του 
 Με πολλαπλασιασμό κατά μέλη:
Με πολλαπλασιασμό κατά μέλη: 
 Αν
Αν  το σύστημα είναι αδύνατο.
το σύστημα είναι αδύνατο. Αν
Αν  τότε το σύστημα λύνεται κατά περίπτωση (δεν έχει πάντα λύση).
τότε το σύστημα λύνεται κατά περίπτωση (δεν έχει πάντα λύση). Αν
Αν  τότε
τότε  και διαιρώντας με καθεμία από τις εξισώσεις του συστήματος βρίσκουμε τους
και διαιρώντας με καθεμία από τις εξισώσεις του συστήματος βρίσκουμε τους 
 , η οποία απεικονίζεται στο τρισδιάστατο γράφημα που επισυνάπτω.
, η οποία απεικονίζεται στο τρισδιάστατο γράφημα που επισυνάπτω. 

 , (4) – (2)
, (4) – (2)  , (4) – (3)
, (4) – (3) 
 πραγματικούς αριθμούς.
πραγματικούς αριθμούς. .
. δηλαδή αν ένας ή τρεις από τους αριθμούς
δηλαδή αν ένας ή τρεις από τους αριθμούς  είναι αρνητικοί και οι άλλοι θετικοί, τότε το σύστημα είναι αδύνατο.
είναι αρνητικοί και οι άλλοι θετικοί, τότε το σύστημα είναι αδύνατο. τότε
τότε  .
.
 και από (4) : (3) έχουμε
και από (4) : (3) έχουμε 
 τότε
τότε  άρα
άρα  , οπότε
, οπότε 
 ,
,  και από (5) : (3)
και από (5) : (3)  .
. τότε
τότε  άρα
άρα  , οπότε επίσης είναι
, οπότε επίσης είναι 
 , από (5) : (2)
, από (5) : (2) 
 .
. , τότε
, τότε  ,
,  και
και  .
. αδύνατο. Πράγματι
αδύνατο. Πράγματι  .
. ή
ή  .
. τότε
τότε  και
και  .
. τότε
τότε  και
και  .
. τότε
τότε  και
και  .
. , τότε
, τότε  ή
ή  ή
ή  .
.Γιώργο, να είσαι καλά Φίλε!Γιώργος Ρίζος έγραψε: ↑Κυρ Ιουν 07, 2020 10:50 amΚαλημέρα σε όλους. Γράφω κάπως πιο αναλυτικά τις δυνατές περιπτώσεις στο 2ο σύστημα. Στο πρώτο έδωσε απάντηση ο Γιώργος παραπάνω. Να σημειώσω απλώς ότι έχει πάντα λύση στο, η οποία απεικονίζεται στο τρισδιάστατο γράφημα που επισυνάπτω.
Ουφ.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες