22591
α) Να αποδείξετε ότι η εξίσωση της υπερβολής που τέμνει τον άξονα

στα σημεία

και διέρχεται από το σημείο

είναι η

(Μονάδες 10)
β) Να βρείτε την εξίσωση του κύκλου

με διάμετρο το τμήμα

(Μονάδες 5)
γ) Να αποδείξετε ότι οι μοναδικές κοινές εφαπτόμενες της υπερβολής

και του κύκλου

είναι οι ευθείες

και

. (Μονάδες 10)
ΛΥΣΗ
Με την παραδοχή ότι η υπερβολή έχει κέντρο την αρχή των αξόνων και άξονα συμμετρίας τον

έχουμε:
α) Έστω

η εξίσωση της υπερβολής. Τα σημεία

είναι οι κορυφές της, οπότε

. Οι συντεταγμένες του σημείου

επαληθεύουν την εξίσωση, επομένως:

Ώστε,

, όποτε η εξίσωση της υπερβολής είναι η

β) Ο κύκλος έχει κέντρο το μέσο του

που είναι το σημείο

και ακτίνα ίση με

, επομένως η εξίσωσή του είναι


- 22591.png (9.17 KiB) Προβλήθηκε 3559 φορές
γ) Έστω

μια κοινή εφαπτομένη των δύο κωνικών τομών, που εφάπτεται του κύκλου στο σημείο

και της υπερβολής στο

. Ισχύουν οι σχέσεις

Αφού η

εφάπτεται του κύκλου στο

έχει εξίσωση

Αφού η

εφάπτεται στην υπερβολή στο

έχει εξίσωση
 1ος τρόπος.
1ος τρόπος. Η απόσταση της ευθείας

από το κέντρο

του κύκλου είναι ίση με την ακτίνα του
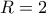
:

Το σύστημα των εξισώσεων

δίνει

, επομένως έχει λύσεις

ή

.
Στην πρώτη περίπτωση από την

η κοινή εφαπτόμενη είναι η

Στην δεύτερη περίπτωση από την

η κοινή εφαπτόμενη είναι η
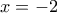 2oς τρόπος.
2oς τρόπος. Οι εξισώσεις

και

παριστάνουν την ίδια ευθεία. Έστω ότι δεν είναι της μορφής

. Από την

συμπεραίνουμε ότι τέμνει τον άξονα των

στο σημείο

. Από την

συμπεραίνουμε ότι θα τον τέμνει στο σημείο

. Τα δύο αυτά σημεία συμπίπτουν, επομένως

. Οι εξισώσεις

και

τώρα γράφονται αντίστοιχα

και παριστάνουν την ίδια ευθεία όταν

άτοπο, γιατί θα πρέπει να είναι της μορφής

. Άρα, οι κοινές εφαπτόμενες είναι της μορφής

. Αυτές είναι προφανώς μόνο οι
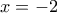
και
 3ος τρόπος.
3ος τρόπος. Έστω ότι έχουμε εφαπτόμενη της μορφής

Το σύστημα των

και

έχει μοναδική λύση. Επομένως η εξίσωση

έχει διακρίνουσα μηδέν:

Ομοίως και το σύστημα των

και

έχει μοναδική λύση, επομένως και η εξίσωση

έχει διακρίνουσα μηδέν:

Οι ισότητες

και

με αφαίρεση κατά μέλη δίνουν 5=0, άτοπο. Επομένως δεν υπάρχουν εφαπτόμενες της μορφής

. Άρα υπάρχουν μόνο της μορφής

. Αυτές είναι προφανώς οι
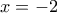
και

 ,
, .
. , με
, με  , παριστάνει κύκλο. Κατόπιν να βρείτε τι παριστάνει η εξίσωση, όταν
, παριστάνει κύκλο. Κατόπιν να βρείτε τι παριστάνει η εξίσωση, όταν  . (Μονάδες 12)
. (Μονάδες 12)  οι κύκλοι που προκύπτουν από την παραπάνω εξίσωση όταν
οι κύκλοι που προκύπτουν από την παραπάνω εξίσωση όταν  και
και  αντίστοιχα.
αντίστοιχα.  και
και  εφάπτονται εξωτερικά. (Μονάδες 6)
εφάπτονται εξωτερικά. (Μονάδες 6) 

 και ακτίνα
και ακτίνα 
 τότε
τότε  και η εξίσωση παριστάνει το σημείο
και η εξίσωση παριστάνει το σημείο 
 και
και  έχουμε αντίστοιχα τις εξισώσεις των κύκλων:
έχουμε αντίστοιχα τις εξισώσεις των κύκλων: με κέντρο
με κέντρο  και ακτίνα
και ακτίνα 
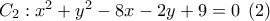 με κέντρο
με κέντρο  και ακτίνα
και ακτίνα 

 έτσι οι κύκλοι
έτσι οι κύκλοι  και
και  εφάπτονται εξωτερικά
εφάπτονται εξωτερικά




 εφάπτονται στο σημείο
εφάπτονται στο σημείο 

 και προαιρετικά μπορεί η δημοσίεση να περιλαμβάνει τη λύση γραμμένη και σε Mathtype.
και προαιρετικά μπορεί η δημοσίεση να περιλαμβάνει τη λύση γραμμένη και σε Mathtype. στα σημεία
στα σημεία  και διέρχεται από το σημείο
και διέρχεται από το σημείο  είναι η
είναι η  (Μονάδες 10)
(Μονάδες 10) με διάμετρο το τμήμα
με διάμετρο το τμήμα  (Μονάδες 5)
(Μονάδες 5) και του κύκλου
και του κύκλου  και
και  . (Μονάδες 10)
. (Μονάδες 10) η εξίσωση της υπερβολής. Τα σημεία
η εξίσωση της υπερβολής. Τα σημεία  . Οι συντεταγμένες του σημείου
. Οι συντεταγμένες του σημείου 
 , όποτε η εξίσωση της υπερβολής είναι η
, όποτε η εξίσωση της υπερβολής είναι η  που είναι το σημείο
που είναι το σημείο  και ακτίνα ίση με
και ακτίνα ίση με  , επομένως η εξίσωσή του είναι
, επομένως η εξίσωσή του είναι 
 μια κοινή εφαπτομένη των δύο κωνικών τομών, που εφάπτεται του κύκλου στο σημείο
μια κοινή εφαπτομένη των δύο κωνικών τομών, που εφάπτεται του κύκλου στο σημείο  και της υπερβολής στο
και της υπερβολής στο  . Ισχύουν οι σχέσεις
. Ισχύουν οι σχέσεις


 από το κέντρο
από το κέντρο 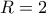 :
:
 δίνει
δίνει  , επομένως έχει λύσεις
, επομένως έχει λύσεις  ή
ή  .
. 
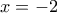
 και
και  . Από την
. Από την  στο σημείο
στο σημείο  . Από την
. Από την  . Τα δύο αυτά σημεία συμπίπτουν, επομένως
. Τα δύο αυτά σημεία συμπίπτουν, επομένως  . Οι εξισώσεις
. Οι εξισώσεις  και παριστάνουν την ίδια ευθεία όταν
και παριστάνουν την ίδια ευθεία όταν  άτοπο, γιατί θα πρέπει να είναι της μορφής
άτοπο, γιατί θα πρέπει να είναι της μορφής  . Άρα, οι κοινές εφαπτόμενες είναι της μορφής
. Άρα, οι κοινές εφαπτόμενες είναι της μορφής  Το σύστημα των
Το σύστημα των  και
και  έχει μοναδική λύση. Επομένως η εξίσωση
έχει μοναδική λύση. Επομένως η εξίσωση

 και
και 

 και
και  με αφαίρεση κατά μέλη δίνουν 5=0, άτοπο. Επομένως δεν υπάρχουν εφαπτόμενες της μορφής
με αφαίρεση κατά μέλη δίνουν 5=0, άτοπο. Επομένως δεν υπάρχουν εφαπτόμενες της μορφής  . Άρα υπάρχουν μόνο της μορφής
. Άρα υπάρχουν μόνο της μορφής  θεωρούμε τα σημεία
θεωρούμε τα σημεία  για τα οποία ισχύει η ισότητα
για τα οποία ισχύει η ισότητα 
 και
και  .
. ανήκουν στον κύκλο
ανήκουν στον κύκλο  (Μονάδες 11)
(Μονάδες 11) και
και  είναι τα σημεία τομής του κύκλου
είναι τα σημεία τομής του κύκλου  και εστίες τα σημεία
και εστίες τα σημεία  και
και  . (Μονάδες 10)
. (Μονάδες 10) ,οπότε
,οπότε
 , εστιακή απόσταση
, εστιακή απόσταση  , οπότε ο μικρός ημιάξονας είναι
, οπότε ο μικρός ημιάξονας είναι  . Επομένως η εξίσωσή της είναι
. Επομένως η εξίσωσή της είναι 
 ,
,  .
.  . (Μονάδες 5)
. (Μονάδες 5)  του
του  ως προς την ευθεία
ως προς την ευθεία  . (Μονάδες 5)
. (Μονάδες 5) 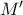 κινείται, για τις διάφορες τιμές του
κινείται, για τις διάφορες τιμές του  , στην ευθεία
, στην ευθεία  . (Μονάδες 5)
. (Μονάδες 5)  και
και  , τότε
, τότε  τέμνει την ευθεία
τέμνει την ευθεία  , το
, το  και επειδή ανήκει στην ευθεία
και επειδή ανήκει στην ευθεία 
 με
με  ,
,  η
η 

 βρίσκουμε ότι:
βρίσκουμε ότι: και
και  , οπότε
, οπότε 
 και
και  θα έχουμε:
θα έχουμε: