 είναι παραγωγίσιμη σε ένα σημείο
είναι παραγωγίσιμη σε ένα σημείο  τότε είναι και συνεχής στο σημείο αυτό.
τότε είναι και συνεχής στο σημείο αυτό.β) i) Να αποδείξετε ότι
 για κάθε
για κάθε 
ii) Έστω συνάρτηση
 παραγωγίσιμη στο
παραγωγίσιμη στο  για την οποία ισχύει
για την οποία ισχύει ![\displaystyle{{{\left[ f(x) \right]}^{5}}+2{{\left[ f(x) \right]}^{3}}+3f(x)=(x+1)\ln (x+1)-\frac{4}{5}x-\frac{{{x}^{2}}}{2}+\frac{{{x}^{3}}}{6}+182} \displaystyle{{{\left[ f(x) \right]}^{5}}+2{{\left[ f(x) \right]}^{3}}+3f(x)=(x+1)\ln (x+1)-\frac{4}{5}x-\frac{{{x}^{2}}}{2}+\frac{{{x}^{3}}}{6}+182}](/forum/ext/geomar/texintegr/latexrender/pictures/80d4bd15e817a9fbfdc56d9ad766f5f6.png)
για κάθε
 . Να αποδείξετε ότι η
. Να αποδείξετε ότι η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
2. α) Δίνονται τα σημεία του επιπέδου

i) Να βρείτε την εξίσωση της ευθείας που διέρχεται από το
 και είναι κάθετη στην ευθεία
και είναι κάθετη στην ευθεία  .
.ii) Έστω
 ο κύκλος με κέντρο το σημείο
ο κύκλος με κέντρο το σημείο  και ακτίνα
και ακτίνα  .
.Να βρείτε τις συντεταγμένες των σημείων τομής της ευθείας
 με τον παραπάνω κύκλο.
με τον παραπάνω κύκλο.β) Έστω
 ένας δειγματικός χώρος με
ένας δειγματικός χώρος με 
i) Να βρείτε το

ii) Έστω η συνάρτηση
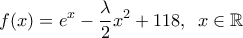 με
με  .
.Θεωρούμε το ενδεχόμενο
 η γραφική παράσταση της
η γραφική παράσταση της  έχει σημείο καμπής το
έχει σημείο καμπής το  .
. Να βρείτε την πιθανότητα του ενδεχομένου
 .
.3. α) Δίνεται η συνάρτηση
 και
και  . Να βρείτε την τιμή του
. Να βρείτε την τιμή του  ώστε να ισχύει
ώστε να ισχύει  για κάθε
για κάθε 
β) Δίνεται η συνάρτηση

i) Να μελετήσετε ως προς την μονοτονία τη συνάρτηση
 και να αποδείξετε ότι
και να αποδείξετε ότι  για κάθε
για κάθε ![\displaystyle{x \in [1,3]} \displaystyle{x \in [1,3]}](/forum/ext/geomar/texintegr/latexrender/pictures/2413aa9c530c98a4d88bc3b54ce11c71.png)
ii) Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της συνάρτησης
 , τον άξονα
, τον άξονα  και τις ευθείες
και τις ευθείες 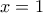 και
και  .
.4. α) Έστω
 ένας
ένας  πίνακας για τον οποίο ισχύει
πίνακας για τον οποίο ισχύει  όπου
όπου  ο
ο  μοναδιαίος πίνακας
μοναδιαίος πίνακαςi) Να αποδείξετε ότι

ii) Έστω
 πίνακας για τον οποίο ισχύει
πίνακας για τον οποίο ισχύει  . Να αποδείξετε ότι
. Να αποδείξετε ότι 
β) Θεωρούμε παραγωγίσιμη συνάρτηση
 με πεδίο ορισμού το
με πεδίο ορισμού το  και το σύστημα
και το σύστημα  με αγνώστους
με αγνώστους  .
.Υποθέτουμε ότι το σύστημα έχει και μη μηδενικές λύσεις. Να αποδείξετε ότι :
i)
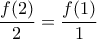
ii) Η εξίσωση
 έχει μια τουλάχιστον ρίζα στο διάστημα
έχει μια τουλάχιστον ρίζα στο διάστημα  .
.
 , παραγωγίσιμη με
, παραγωγίσιμη με 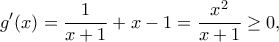 για
για  με
με 
 είναι γνησίως αύξουσα για
είναι γνησίως αύξουσα για  με
με  , άρα
, άρα  για
για 
 παραγωγίσιμη, παραγωγίζοντας τη δοσμένη είναι
παραγωγίσιμη, παραγωγίζοντας τη δοσμένη είναι  αφού
αφού  και
και  δηλαδή η
δηλαδή η 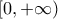

 (1)
(1) (2)
(2)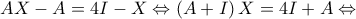




 (3)
(3) και αφαιρώντας την 2η γραμμή η
και αφαιρώντας την 2η γραμμή η  γίνεται:
γίνεται:![\displaystyle{\left| {\begin{array}{*{20}{c}}
{2f\left( 1 \right) - f\left( 2 \right)}&0&0\\
{f\left( 2 \right)}&2&2\\
2&{f\left( 2 \right)}&{2f\left( 1 \right)}
\end{array}} \right| = 0 \Leftrightarrow \left[ {2f\left( 1 \right) - f\left( 2 \right)} \right]\left| {\begin{array}{*{20}{c}}
2&2\\
{f\left( 2 \right)}&{2f\left( 1 \right)}
\end{array}} \right| = 0 \Leftrightarrow } \displaystyle{\left| {\begin{array}{*{20}{c}}
{2f\left( 1 \right) - f\left( 2 \right)}&0&0\\
{f\left( 2 \right)}&2&2\\
2&{f\left( 2 \right)}&{2f\left( 1 \right)}
\end{array}} \right| = 0 \Leftrightarrow \left[ {2f\left( 1 \right) - f\left( 2 \right)} \right]\left| {\begin{array}{*{20}{c}}
2&2\\
{f\left( 2 \right)}&{2f\left( 1 \right)}
\end{array}} \right| = 0 \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/2e6c095c5157efaff57213a86f5f8c46.png)
![\displaystyle{\left[ {2f\left( 1 \right) - f\left( 2 \right)} \right]\left[ {4f\left( 1 \right) - 2f\left( 2 \right)} \right] = 0 \Leftrightarrow 2{\left[ {2f\left( 1 \right) - f\left( 2 \right)} \right]^2} = 0 \Leftrightarrow } \displaystyle{\left[ {2f\left( 1 \right) - f\left( 2 \right)} \right]\left[ {4f\left( 1 \right) - 2f\left( 2 \right)} \right] = 0 \Leftrightarrow 2{\left[ {2f\left( 1 \right) - f\left( 2 \right)} \right]^2} = 0 \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/08da16750bd4daea6c9ed1bf00fd105d.png)

 με
με 
 είναι συνεχής στο
είναι συνεχής στο ![\left[ {1,2} \right] \left[ {1,2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/920e557d494338f99247a92f36565036.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 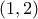 ως πηλίκο συνεχών και παραγωγίσιμων συναρτήσεων.
ως πηλίκο συνεχών και παραγωγίσιμων συναρτήσεων. και
και 
 .
. , υπάρχει ένα τουλάχιστον
, υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε 
 είναι η
είναι η

 συμβολίσουμε τον συντελεστή διεύθυνσης της ζητούμενης ευθείας, τότε,
συμβολίσουμε τον συντελεστή διεύθυνσης της ζητούμενης ευθείας, τότε,
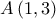 , η εξίσωση της δίνεται από την
, η εξίσωση της δίνεται από την





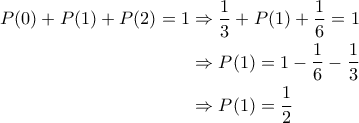
 έχουμε,
έχουμε,
 τότε
τότε  με αποτέλεσμα η
με αποτέλεσμα η  , τότε,
, τότε, 

 , τότε,
, τότε,  .
. .
.

 για κάθε
για κάθε 
![\displaystyle{f'(x)=[sin^{2}(\alpha x)]'=2sin(\alpha x).(sin\alpha x)'=2sin(\alpha x).cos(\alpha x).(\alpha x)'=2\alpha.sin(\alpha x).cos(\alpha x)=\alpha sin(2\alpha x)} \displaystyle{f'(x)=[sin^{2}(\alpha x)]'=2sin(\alpha x).(sin\alpha x)'=2sin(\alpha x).cos(\alpha x).(\alpha x)'=2\alpha.sin(\alpha x).cos(\alpha x)=\alpha sin(2\alpha x)}](/forum/ext/geomar/texintegr/latexrender/pictures/4476479c0958379c76eaecccaf9ba111.png)
![\displaystyle{f''(x)=[\alpha sin(2\alpha x)]'=\alpha (sin(2\alpha x))'=\alpha cos(2\alpha x).(2\alpha x)'=2\alpha ^{2}cos(2\alpha x)\Leftrightarrow f''(x)=2\alpha ^{2}cos(2\alpha x)} \displaystyle{f''(x)=[\alpha sin(2\alpha x)]'=\alpha (sin(2\alpha x))'=\alpha cos(2\alpha x).(2\alpha x)'=2\alpha ^{2}cos(2\alpha x)\Leftrightarrow f''(x)=2\alpha ^{2}cos(2\alpha x)}](/forum/ext/geomar/texintegr/latexrender/pictures/0f5f81b1a74db0a002f8f7d3928c0751.png)

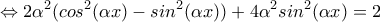



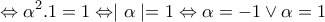


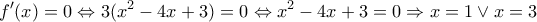
![\displaystyle{(-\infty ,1]\cup [3,+\infty )} \displaystyle{(-\infty ,1]\cup [3,+\infty )}](/forum/ext/geomar/texintegr/latexrender/pictures/ce52d460956dc79a98e41cd11a37b31d.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![\displaystyle{[1,3]} \displaystyle{[1,3]}](/forum/ext/geomar/texintegr/latexrender/pictures/c9d58c1778b53af992ebce56b3819be1.png)
 Αλλά
Αλλά 



![\displaystyle{[\frac{x^{4}}{4}]_{1}^{3}-6[\frac{x^{3}}{3}]_{1}^{3}+9[\frac{x^{2}}{2}]_{1}^{3}+2=...=6} \displaystyle{[\frac{x^{4}}{4}]_{1}^{3}-6[\frac{x^{3}}{3}]_{1}^{3}+9[\frac{x^{2}}{2}]_{1}^{3}+2=...=6}](/forum/ext/geomar/texintegr/latexrender/pictures/cf3fb0b07cdcd2813993e5413db05414.png) τ.μ.
τ.μ.