 είναι πίνακας
είναι πίνακας  και υπάρχουν πραγματικοί αριθμοί
και υπάρχουν πραγματικοί αριθμοί 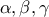 με
με  για τους οποίους ισχύει ότι
για τους οποίους ισχύει ότι  όπου
όπου  ο μοναδιαίος και ο μηδενικός πίνακας
ο μοναδιαίος και ο μηδενικός πίνακας  αντιστοίχως
αντιστοίχωςνα αποδείξετε ότι
 είναι αντιστρέψιμος .
είναι αντιστρέψιμος .β) Αν
![A =\left[ \begin{matrix}
2 & 4 \\
-1 & 3 \\
\end{matrix} \right] A =\left[ \begin{matrix}
2 & 4 \\
-1 & 3 \\
\end{matrix} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/cd7792c96f5121c2aa2f8eb3a9fabcc4.png) και
και  ο μοναδιαίος και ο μηδενικός πίνακας
ο μοναδιαίος και ο μηδενικός πίνακας  αντιστοίχως,
αντιστοίχως, να βρείτε όλες τις τριάδες
 πραγματικών αριθμών για τις οποίες ισχύει ότι
πραγματικών αριθμών για τις οποίες ισχύει ότι  .
.2. α) Να αποδείξετε ότι :
''Αν οι συναρτήσεις
 είναι ορισμένες στο διάστημα
είναι ορισμένες στο διάστημα  και παραγωγίσιμες στο
και παραγωγίσιμες στο  τότε η
τότε η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και είναι
και είναι 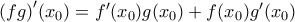 ''.
''.β) Δίνεται η συνάρτηση
 η οποία είναι ορισμένη στο
η οποία είναι ορισμένη στο  , δυο φορές παραγωγίσιμη σ’ αυτό και ισχύει
, δυο φορές παραγωγίσιμη σ’ αυτό και ισχύει  .
. Αν
 είναι μια συνάρτηση με
είναι μια συνάρτηση με 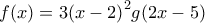 να αποδείξετε ότι η
να αποδείξετε ότι η  είναι δυο φορές παραγωγίσιμη στο
είναι δυο φορές παραγωγίσιμη στο 
και να υπολογίσετε την
 .
.3. Έστω
 πραγματικός αριθμός και
πραγματικός αριθμός και  η συνάρτηση με
η συνάρτηση με  .
. Να αποδείξετε ότι η γραφική παράσταση της
 δεν έχει σημεία καμπής.
δεν έχει σημεία καμπής.4. α) Έστω μια συνάρτηση
 συνεχής στο διάστημα
συνεχής στο διάστημα  και
και  με
με 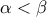 .
. Αν
 είναι μια παράγουσα της
είναι μια παράγουσα της  στο
στο ![\displaystyle{[\alpha ,\beta]} \displaystyle{[\alpha ,\beta]}](/forum/ext/geomar/texintegr/latexrender/pictures/52427afc2dcbdbb11264309a8f654c9a.png) τότε να αποδείξετε ότι
τότε να αποδείξετε ότι  .
.β) Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται μεταξύ της γραφικής παράστασης της συνάρτησης
 με
με 
του άξονα
 και των ευθειών με εξισώσεις
και των ευθειών με εξισώσεις 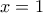 και
και  .
.

 είναι αντιστρέψιμος με
είναι αντιστρέψιμος με 
![{{\rm A}^2} = \left[ {\begin{array}{*{20}{c}}
2&4\\
{ - 1}&3
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
2&4\\
{ - 1}&3
\end{array}} \right] \Rightarrow {{\rm A}^2} = \left[ {\begin{array}{*{20}{c}}
0&{20}\\
{ - 5}&5
\end{array}} \right] {{\rm A}^2} = \left[ {\begin{array}{*{20}{c}}
2&4\\
{ - 1}&3
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
2&4\\
{ - 1}&3
\end{array}} \right] \Rightarrow {{\rm A}^2} = \left[ {\begin{array}{*{20}{c}}
0&{20}\\
{ - 5}&5
\end{array}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/021bf0d317242e337ce826ac4d3f77ea.png)
![\kappa {{\rm A}^2} + 3\lambda {\rm A} - \mu {\rm I} = {\rm O} \Rightarrow \kappa \left[ {\begin{array}{*{20}{c}}
0&{20}\\
{ - 5}&5
\end{array}} \right] + 3\lambda \left[ {\begin{array}{*{20}{c}}
2&4\\
{ - 1}&3
\end{array}} \right] - \mu \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right] = {\rm O} \Rightarrow \kappa {{\rm A}^2} + 3\lambda {\rm A} - \mu {\rm I} = {\rm O} \Rightarrow \kappa \left[ {\begin{array}{*{20}{c}}
0&{20}\\
{ - 5}&5
\end{array}} \right] + 3\lambda \left[ {\begin{array}{*{20}{c}}
2&4\\
{ - 1}&3
\end{array}} \right] - \mu \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right] = {\rm O} \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/d87986062ce309f89f10fd9646dd45fb.png)
![\left[ {\begin{array}{*{20}{c}}
0&{20\kappa }\\
{ - 5\kappa }&{5\kappa }
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{6\lambda }&{12\lambda }\\
{ - 3\lambda }&{9\lambda }
\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}
\mu &0\\
0&\mu
\end{array}} \right] = {\rm O} \Rightarrow \left[ {\begin{array}{*{20}{c}}
0&{20\kappa }\\
{ - 5\kappa }&{5\kappa }
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{6\lambda }&{12\lambda }\\
{ - 3\lambda }&{9\lambda }
\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}
\mu &0\\
0&\mu
\end{array}} \right] = {\rm O} \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/39a0acfb2c624ee2862e0ba6ef8a8f9d.png)
![\left[ {\begin{array}{*{20}{c}}
{6\lambda - \mu }&{20\kappa + 12\lambda }\\
{ - 5\kappa - 3\lambda }&{5\kappa + 9\lambda - \mu }
\end{array}} \right] = {\rm O} \Leftrightarrow \left\{ \begin{array}{l}
6\lambda - \mu = 0\\
- 5\kappa - 3\lambda = 0\\
20\kappa + 12\lambda = 0\\
5\kappa + 9\lambda - \mu = 0
\end{array} \right.\mathop \Rightarrow \limits_{:4}^{ \cdot \left( { - 1} \right)} \left\{ \begin{array}{l}
6\lambda - \mu = 0\quad \;\;(1)\\
5\kappa + 3\lambda = 0\quad (2)\\
5\kappa + 3\lambda = 0\\
5\kappa + 9\lambda - \mu = 0\;(3)
\end{array} \right. \left[ {\begin{array}{*{20}{c}}
{6\lambda - \mu }&{20\kappa + 12\lambda }\\
{ - 5\kappa - 3\lambda }&{5\kappa + 9\lambda - \mu }
\end{array}} \right] = {\rm O} \Leftrightarrow \left\{ \begin{array}{l}
6\lambda - \mu = 0\\
- 5\kappa - 3\lambda = 0\\
20\kappa + 12\lambda = 0\\
5\kappa + 9\lambda - \mu = 0
\end{array} \right.\mathop \Rightarrow \limits_{:4}^{ \cdot \left( { - 1} \right)} \left\{ \begin{array}{l}
6\lambda - \mu = 0\quad \;\;(1)\\
5\kappa + 3\lambda = 0\quad (2)\\
5\kappa + 3\lambda = 0\\
5\kappa + 9\lambda - \mu = 0\;(3)
\end{array} \right.](/forum/ext/geomar/texintegr/latexrender/pictures/454402273a0a8d35d84b8996659b41f1.png)
 και
και 


 στο
στο ![\displaystyle{[1,3]} \displaystyle{[1,3]}](/forum/ext/geomar/texintegr/latexrender/pictures/c9d58c1778b53af992ebce56b3819be1.png) διότι
διότι  όταν
όταν ![\displaystyle{x \in [1,3]} \displaystyle{x \in [1,3]}](/forum/ext/geomar/texintegr/latexrender/pictures/2413aa9c530c98a4d88bc3b54ce11c71.png)
![\displaystyle{\int_{1 }^{3 }{|f(x)|}dx=\int_{1 }^{3 }{f(x)}dx=\int\limits_{1 }^{3 }{{{x}^{2}}{{e}^{x}}}dx =\int_{1 }^{3 }{{{x}^{2}}{({e}^{x})'}}dx=[{x}^{2}}{{e}^{x}]_{1}^{3}-\int_{1 }^{3 }{{({x}^{2})'}{{e}^{x}}}dx} \displaystyle{\int_{1 }^{3 }{|f(x)|}dx=\int_{1 }^{3 }{f(x)}dx=\int\limits_{1 }^{3 }{{{x}^{2}}{{e}^{x}}}dx =\int_{1 }^{3 }{{{x}^{2}}{({e}^{x})'}}dx=[{x}^{2}}{{e}^{x}]_{1}^{3}-\int_{1 }^{3 }{{({x}^{2})'}{{e}^{x}}}dx}](/forum/ext/geomar/texintegr/latexrender/pictures/deae9c1d3b9fd937c7ee4b20be4b9baf.png)
![\displaystyle{=3^2e^3-1^2e^1-\int_{1 }^{3 }{2x}{{e}^{x}}}dx}=9e^3-e-\int_{1 }^{3 }{2x}{({e}^{x})'}}dx=9e^3-e-\left([2x}{{e}^{x}]_{1}^{3}-\int_{1 }^{3 }{(2x})'{{e}^{x}}}dx\right)} \displaystyle{=3^2e^3-1^2e^1-\int_{1 }^{3 }{2x}{{e}^{x}}}dx}=9e^3-e-\int_{1 }^{3 }{2x}{({e}^{x})'}}dx=9e^3-e-\left([2x}{{e}^{x}]_{1}^{3}-\int_{1 }^{3 }{(2x})'{{e}^{x}}}dx\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/d69e7b07cb035b68b9b93be0ff69df47.png)
![\displaystyle{=9e^3-e-[2x{{e}^{x}]_{1}^{3}+\int_{1 }^{3 }{2}{{e}^{x}}}dx=9e^3-e-(2\cdot 3 e^3-2\cdot 1e^1)+[2{{e}^{x}]_{1}^{3}=} \displaystyle{=9e^3-e-[2x{{e}^{x}]_{1}^{3}+\int_{1 }^{3 }{2}{{e}^{x}}}dx=9e^3-e-(2\cdot 3 e^3-2\cdot 1e^1)+[2{{e}^{x}]_{1}^{3}=}](/forum/ext/geomar/texintegr/latexrender/pictures/61bd37e27e170533edb380be12864790.png)

 , με
, με
 είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο 

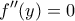 .
. έχουμε
έχουμε![\displaystyle{\begin{aligned}f''(x)=0&\Leftrightarrow 4\,x^2+4\alpha\,x+\left(2\alpha^2-4\alpha+5\right)=0\\&\Leftrightarrow x^2+\alpha\,x+\frac{2\alpha^2-4\alpha+5}{4}=0\\&\Leftrightarrow \left(x+\frac{\alpha}{2}\right)^2=\frac{\alpha^2}{4}-\frac{2\alpha^2-4\alpha+5}{4}\\&\Leftrightarrow \left(x+\frac{\alpha}{2}\right)^2=\left(-\frac{1}{4}\right)\left[\left(\alpha-2\right)^2+1\right]\\&\Leftrightarrow x\in \varnothing \end{aligned}} \displaystyle{\begin{aligned}f''(x)=0&\Leftrightarrow 4\,x^2+4\alpha\,x+\left(2\alpha^2-4\alpha+5\right)=0\\&\Leftrightarrow x^2+\alpha\,x+\frac{2\alpha^2-4\alpha+5}{4}=0\\&\Leftrightarrow \left(x+\frac{\alpha}{2}\right)^2=\frac{\alpha^2}{4}-\frac{2\alpha^2-4\alpha+5}{4}\\&\Leftrightarrow \left(x+\frac{\alpha}{2}\right)^2=\left(-\frac{1}{4}\right)\left[\left(\alpha-2\right)^2+1\right]\\&\Leftrightarrow x\in \varnothing \end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/e31fc465f5c4d0651cf42b0853d726ee.png)