 όπου
όπου  και
και  και
και  . Να δώσετε τους παρακάτω ορισμούς:
. Να δώσετε τους παρακάτω ορισμούς:i) Πότε η
 λέγεται γνησίως αύξουσα;
λέγεται γνησίως αύξουσα;ii) Πότε η
 λέγεται γνησίως φθίνουσα;
λέγεται γνησίως φθίνουσα;iii) Πότε η
 λέγεται αύξουσα;
λέγεται αύξουσα;iv) Πότε η
 λέγεται φθίνουσα;
λέγεται φθίνουσα;v) Πότε η
 λέγεται « συνάρτηση επί»;
λέγεται « συνάρτηση επί»;β) i) Να βρείτε την εξίσωση της ευθείας που διέρχεται από τα σημεία
 και
και 
ii) Να βρείτε το
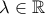 έτσι ώστε η παραπάνω ευθεία να διέρχεται από το σημείο
έτσι ώστε η παραπάνω ευθεία να διέρχεται από το σημείο  .
.2. α) Έστω
 η μέση τιμή της μεταβλητής
η μέση τιμή της μεταβλητής  ως προς τη οποία εξετάζουμε ένα δείγμα.
ως προς τη οποία εξετάζουμε ένα δείγμα. Να αποδειχθεί ότι η μέση τιμή
 της μεταβλητής
της μεταβλητής  (
( ) είναι
) είναι  .
.β) Να αποδειχθεί ότι

3. Να βρεθούν οι τιμές των
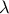 και
και  για τις οποίες τα συστήματα
για τις οποίες τα συστήματα  και
και  είναι συγχρόνως αδύνατα.
είναι συγχρόνως αδύνατα.4. α) Να αποδειχθεί ότι αν μια συνάρτηση
 είναι παραγωγίσιμη σε ένα σημείο
είναι παραγωγίσιμη σε ένα σημείο  τότε είναι συνεχής στο σημείο αυτό.
τότε είναι συνεχής στο σημείο αυτό.β) Έστω
 η γραφική παράσταση της συνάρτησης f με
η γραφική παράσταση της συνάρτησης f με  .
. Να προσδιορίσετε τα
 έτσι ώστε το σημείο
έτσι ώστε το σημείο  να ανήκει στην
να ανήκει στην 
και η εφαπτομένη της
 στο σημείο
στο σημείο  να έχει συντελεστή διευθύνσεως τον αριθμό
να έχει συντελεστή διευθύνσεως τον αριθμό  .
.
 τις γραμμές, τότε εκτελώντας τις γραμμοπράξεις
τις γραμμές, τότε εκτελώντας τις γραμμοπράξεις η ορίζουσα γίνεται
η ορίζουσα γίνεται
 .
.

 ισχύει:
ισχύει: 