 . Να υπολογισθεί ο πίνακας
. Να υπολογισθεί ο πίνακας  .
.β)Έστω
 και
και  ένας πίνακας
ένας πίνακας  . Να βρεθεί ο
. Να βρεθεί ο  αν
αν 
2. Δίνεται η συνάρτηση
 με
με  .
. Να βρεθούν τα διαστήματα μονοτονίας της
 και το είδος μονοτονίας σε καθένα από αυτά, καθώς και τα τοπικά μέγιστα και ελάχιστα.
και το είδος μονοτονίας σε καθένα από αυτά, καθώς και τα τοπικά μέγιστα και ελάχιστα. Επίσης να βρεθούν τα διαστήματα στα οποία η γραφική παράσταση της
 στρέφει
στρέφει α) τα κοίλα άνω
β) τα κοίλα κάτω
Ακόμα να βρεθούν τα ενδεχόμενα σημεία καμπής.
3. α) Έστω η συνάρτηση
 με πεδίο ορισμού
με πεδίο ορισμού  . Να δώσετε τους παρακάτω ορισμούς:
. Να δώσετε τους παρακάτω ορισμούς:i) Πότε η f λέγεται άρτια
ii) Πότε η f λέγεται περιττή
iii) Πότε η f λέγεται περιοδική
iv) Πότε η f λέγεται φραγμένη άνω και
v) Πότε η f λέγεται φραγμένη κάτω
β) Δίνεται η συνάρτηση
 με
με  . Να βρεθεί το σύνολο τιμών της
. Να βρεθεί το σύνολο τιμών της  .
.4. α) Έστω f,g συναρτήσεις που ορίζονται στο διάστημα
 και
και  .
. Αν οι
 είναι παραγωγίσιμες στο
είναι παραγωγίσιμες στο  τότε να αποδειχθεί ότι και η
τότε να αποδειχθεί ότι και η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και είναι
και είναι 
β) Έστω η συνάρτηση
 με
με  .
.Να βρεθεί η εξίσωση της εφαπτομένης της γραφικής παράστασης της
 στο σημείο
στο σημείο  .
.

 ο ζητούμενος πίνακας.Έχουμε:
ο ζητούμενος πίνακας.Έχουμε:






 Βάζουμε όπου χ το -χ και λαμβάνουμε:
Βάζουμε όπου χ το -χ και λαμβάνουμε:
 είναι περριτή και επομένως αρκεί να τη μελετήσουμε στο
είναι περριτή και επομένως αρκεί να τη μελετήσουμε στο 





 ,
, 

![\displaystyle{f(D_{f})=\left[-\frac{3}{2},\frac{3}{2}\right]} \displaystyle{f(D_{f})=\left[-\frac{3}{2},\frac{3}{2}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/32b399430ac71c3cfed4bfa3d4ed92d1.png)
 . Αν
. Αν  . Δηλαδή το
. Δηλαδή το  . Αν
. Αν  τότε για να έχει μία τουλάχιστον ρίζα πραγματική το τριώνυμο, πρέπει
τότε για να έχει μία τουλάχιστον ρίζα πραγματική το τριώνυμο, πρέπει  , δηλαδή πρέπει
, δηλαδή πρέπει  , δηλαδή ισοδύναμα πρέπει
, δηλαδή ισοδύναμα πρέπει 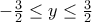 kai επομένως
kai επομένως ![f(R)=[-\frac{3}{2} , \frac{3}{2}] f(R)=[-\frac{3}{2} , \frac{3}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/fb9be9f35271fe05ba0b5d7d69abea0f.png)
 είναι:
είναι: 
 όπου είναι και η ζητούμενη ευθεία.
όπου είναι και η ζητούμενη ευθεία. Θέτουμε
Θέτουμε  με
με 
 ΄
΄ και για
και για ![a\in \left[-\frac{\pi}{4} , \frac{\pi}{4}\right] . a\in \left[-\frac{\pi}{4} , \frac{\pi}{4}\right] .](/forum/ext/geomar/texintegr/latexrender/pictures/c146ad45ac8ffe2a7fa816546f6f2ac6.png) η παράσταση
η παράσταση  παίρνει όλες τις τιμές του διαστήματος
παίρνει όλες τις τιμές του διαστήματος ![\left[-\dfrac{3}{2} , \dfrac{3}{2}\right]. \left[-\dfrac{3}{2} , \dfrac{3}{2}\right].](/forum/ext/geomar/texintegr/latexrender/pictures/024facb678a4ee562d7809fa00bf3ae1.png)
![f(\mathbb{R})=\left[-\dfrac{3}{2} , \dfrac{3}{2}\right]. f(\mathbb{R})=\left[-\dfrac{3}{2} , \dfrac{3}{2}\right].](/forum/ext/geomar/texintegr/latexrender/pictures/f3bb31fd930aafd2814af23fbf643005.png)

 ως πολυωνυμική
ως πολυωνυμική
 ή
ή 


 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle{(-\infty,1]} \displaystyle{(-\infty,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/e1069188bbe9f27b2735887eb0cd2b89.png) και στο
και στο  και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![\displaystyle{[1,3]} \displaystyle{[1,3]}](/forum/ext/geomar/texintegr/latexrender/pictures/c9d58c1778b53af992ebce56b3819be1.png)
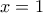 στο
στο ![\displaystyle{(-\infty,3]} \displaystyle{(-\infty,3]}](/forum/ext/geomar/texintegr/latexrender/pictures/8958579cf0ec30c43a758b3af8d15916.png) και τοπικό ελάχιστο για
και τοπικό ελάχιστο για 

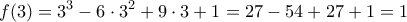
 είναι συνεχής και παραγωγισίμη στο
είναι συνεχής και παραγωγισίμη στο 



 και κοίλη στο
και κοίλη στο ![\displaystyle{(-\infty,2]} \displaystyle{(-\infty,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/43212cdda49a7967e1c6b7f97bf1922d.png)

