 και ονομάζουμε
και ονομάζουμε  τον πρώτο και
τον πρώτο και  το δεύτερο.
το δεύτερο.α) Να αποδείξετε ότι ισχύει
 όπου
όπου  ο πίνακας
ο πίνακας 
β) Να λύσετε την εξίσωση
 (
( )
)2. α) Έστω το σύστημα (
 ) :
) :  με τους
με τους  πραγματικούς αριθμούς.
πραγματικούς αριθμούς. Να αποδείξετε ότι αν ο πίνακας
 είναι αντιστρέψιμος τότε το σύστημα έχει μία μόνο λύση.
είναι αντιστρέψιμος τότε το σύστημα έχει μία μόνο λύση.β) Να λύσετε (και να διερευνήσετε) το σύστημα
 όπου
όπου 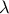 πραγματικός αριθμός.
πραγματικός αριθμός.3. Έστω η πραγματική συνάρτηση
 της πραγματικής μεταβλητής
της πραγματικής μεταβλητής  με
με 
α) Να βρείτε το πεδίο ορισμού και το σύνολο των τιμών της

β) Να εξετάσετε την
 ως προς την μονοτονία σε καθένα από τα διαστήματα
ως προς την μονοτονία σε καθένα από τα διαστήματα ![(0,2] (0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/eb1351ddf84d6ca6e06bbb319592766d.png) και
και 
4. α) Έστω μια πραγματική συνάρτηση
 με πεδίο ορισμού της
με πεδίο ορισμού της  ένα υποσύνολο του
ένα υποσύνολο του  ,
, που περιέχει ένα ανοικτό διάστημα
 με
με  και έστω
και έστω  ένα από τα άκρα του διαστήματος
ένα από τα άκρα του διαστήματος  .
. Τι εννοούμε όταν λέμε ότι η συνάρτηση f έχει όριο στο
 το
το  και τι όταν λέμε ότι η συνάρτηση
και τι όταν λέμε ότι η συνάρτηση  έχει όριο στο
έχει όριο στο  το
το  ;
;β) Έστω η πραγματική συνάρτηση της πραγματικής μεταβλητής
 με
με  να βρείτε το
να βρείτε το  .
.
 και ονομάζουμε
και ονομάζουμε 



![\displaystyle{=\frac{1}{2}\left[\begin{bmatrix}\displaystyle{cosx & sinx}\\ & \\ \displaystyle{sinx & cosx}\end{bmatrix}\cdot\begin{bmatrix}\displaystyle{cosx & sinx}\\ & \\ \displaystyle{sinx & cosx}\end{bmatrix} + \begin{bmatrix}\displaystyle{cosx & -sinx}\\ & \\ \displaystyle{-sinx & cosx}\end{bmatrix}\cdot\begin{bmatrix}\displaystyle{cosx & -sinx}\\ & \\ \displaystyle{-sinx & cosx}\end{bmatrix}\right]=} \displaystyle{=\frac{1}{2}\left[\begin{bmatrix}\displaystyle{cosx & sinx}\\ & \\ \displaystyle{sinx & cosx}\end{bmatrix}\cdot\begin{bmatrix}\displaystyle{cosx & sinx}\\ & \\ \displaystyle{sinx & cosx}\end{bmatrix} + \begin{bmatrix}\displaystyle{cosx & -sinx}\\ & \\ \displaystyle{-sinx & cosx}\end{bmatrix}\cdot\begin{bmatrix}\displaystyle{cosx & -sinx}\\ & \\ \displaystyle{-sinx & cosx}\end{bmatrix}\right]=}](/forum/ext/geomar/texintegr/latexrender/pictures/3511ea33f83e592d8d4737427a94917e.png)
![\displaystyle{=\frac{1}{2}\left[\begin{bmatrix}\displaystyle{1 & sin2x}\\ & \\ \displaystyle{sin2x & 1}\end{bmatrix}+ \begin{bmatrix}\displaystyle{1 & -sin2x}\\ & \\ \displaystyle{-sin2x & 1}\end{bmatrix}\right]=} \displaystyle{=\frac{1}{2}\left[\begin{bmatrix}\displaystyle{1 & sin2x}\\ & \\ \displaystyle{sin2x & 1}\end{bmatrix}+ \begin{bmatrix}\displaystyle{1 & -sin2x}\\ & \\ \displaystyle{-sin2x & 1}\end{bmatrix}\right]=}](/forum/ext/geomar/texintegr/latexrender/pictures/828db75208c86ed9e6a09c228ff69f13.png)



![\displaystyle{\frac{1}{2}\left[\begin{bmatrix}\displaystyle{1 & sin2x}\\ & \\ \displaystyle{sin2x & 1}\end{bmatrix}- \begin{bmatrix}\displaystyle{1 & -sin2x}\\ & \\ \displaystyle{-sin2x & 1}\end{bmatrix}\right]=\begin{bmatrix}\displaystyle{0 & 0}\\ & \\ \displaystyle{0 & 0}\end{bmatrix}} \displaystyle{\frac{1}{2}\left[\begin{bmatrix}\displaystyle{1 & sin2x}\\ & \\ \displaystyle{sin2x & 1}\end{bmatrix}- \begin{bmatrix}\displaystyle{1 & -sin2x}\\ & \\ \displaystyle{-sin2x & 1}\end{bmatrix}\right]=\begin{bmatrix}\displaystyle{0 & 0}\\ & \\ \displaystyle{0 & 0}\end{bmatrix}}](/forum/ext/geomar/texintegr/latexrender/pictures/43a5d218e160a99a36c3a7dc75419790.png)


 ,
, 

 είναι
είναι 
 και, επί πλέον, ότι
και, επί πλέον, ότι
![\displaystyle{f\left(D\left(\psi\right)\right)=\left(\lim_{x\to -\infty}\psi(x),\psi(-2)\right]\cup\left(\lim_{x\to 0^{-}}\psi(x),\psi(-2)\right]\left[\psi(2),\lim_{x\to 0^{+}}\psi(x)\right)\cup\left[\psi(2),\lim_{x\to +\infty}\psi(x)\right) \displaystyle{f\left(D\left(\psi\right)\right)=\left(\lim_{x\to -\infty}\psi(x),\psi(-2)\right]\cup\left(\lim_{x\to 0^{-}}\psi(x),\psi(-2)\right]\left[\psi(2),\lim_{x\to 0^{+}}\psi(x)\right)\cup\left[\psi(2),\lim_{x\to +\infty}\psi(x)\right)](/forum/ext/geomar/texintegr/latexrender/pictures/8d31201730c59efcffa1db80c9a17c54.png) , όπου
, όπου



![\displaystyle{f\left(D\left(\psi\right)\right)=\left(-\infty,-4\right]\cup\left(-\infty,-4\right]\cup\left[4,+\infty\right)\cup\left[4,+\infty\right)=\left(-\infty,-4\right]\cup\left[4,+\infty\right)} \displaystyle{f\left(D\left(\psi\right)\right)=\left(-\infty,-4\right]\cup\left(-\infty,-4\right]\cup\left[4,+\infty\right)\cup\left[4,+\infty\right)=\left(-\infty,-4\right]\cup\left[4,+\infty\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/7444de716f0b1a6f56a1b716127f7339.png)
 .Τότε, υπάρχει
.Τότε, υπάρχει  τέτοιο,
τέτοιο, , οπότε,
, οπότε,![\displaystyle{x+\frac{4}{x}=y\Rightarrow x^2+4=xy\Rightarrow x^2-xy=-4\Rightarrow \left(x-\frac{y}{2}\right)^2=\frac{y^2}{4}-4\Rightarrow \frac{y^2}{4}\geq 4\Rightarrow y^2\geq 16 \Rightarrow y\in\left(-\infty,-4\right]\cup\left[4,+\infty\right)} \displaystyle{x+\frac{4}{x}=y\Rightarrow x^2+4=xy\Rightarrow x^2-xy=-4\Rightarrow \left(x-\frac{y}{2}\right)^2=\frac{y^2}{4}-4\Rightarrow \frac{y^2}{4}\geq 4\Rightarrow y^2\geq 16 \Rightarrow y\in\left(-\infty,-4\right]\cup\left[4,+\infty\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/c65aef98a2f8c75c20b9127a132516c2.png)
![\displaystyle{D\left(\psi\right)\subset \left(-\infty,-4\right]\cup\left[4,+\infty\right)\,\,(I)} \displaystyle{D\left(\psi\right)\subset \left(-\infty,-4\right]\cup\left[4,+\infty\right)\,\,(I)}](/forum/ext/geomar/texintegr/latexrender/pictures/b3fdd9100fb21cf55d5b0b8c7ba05685.png)
![\displaystyle{z\in\left(-\infty,-4\right]\cup\left[4,+\infty\right)} \displaystyle{z\in\left(-\infty,-4\right]\cup\left[4,+\infty\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/fcdaa51fe9cc4934e63a2f92f680ce65.png)
![\displaystyle{z\in\left(-\infty,-4\right]} \displaystyle{z\in\left(-\infty,-4\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/40bb2edf724931606ecbcd58ed0970e2.png)
 ισχύει
ισχύει  , γεγονός που
, γεγονός που

 ισχύει
ισχύει ![\displaystyle{\left(-\infty,-4\right]\cup\left[4,+\infty\right)\subset f\left(D\left(\psi\right)\right)\,\,(II)} \displaystyle{\left(-\infty,-4\right]\cup\left[4,+\infty\right)\subset f\left(D\left(\psi\right)\right)\,\,(II)}](/forum/ext/geomar/texintegr/latexrender/pictures/13ac3203d69269ab52436851ca16768c.png)
 δίνουν
δίνουν ![\displaystyle{f\left(D\left(\psi\right)\right)=\left(-\infty,-4\right]\cup\left[4,+\infty\right)} \displaystyle{f\left(D\left(\psi\right)\right)=\left(-\infty,-4\right]\cup\left[4,+\infty\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/0b760948b9112b8a50a0a950e3975942.png)

 και η ισότητα ισχύει για
και η ισότητα ισχύει για 
 και
και  άρα το
άρα το
![\displaystyle{(-\infty ,-4]\cup [4,+\infty ).} \displaystyle{(-\infty ,-4]\cup [4,+\infty ).}](/forum/ext/geomar/texintegr/latexrender/pictures/2f80be141da5569f0acdf7615a381a7d.png)
 έχουμε
έχουμε  .
. .
.





 Αν
Αν  και
και  , το σύστημα έχει μοναδική λύση
, το σύστημα έχει μοναδική λύση 
 είναι
είναι  , άρα το σύστημα γίνεται
, άρα το σύστημα γίνεται

 της ευθείας
της ευθείας 
 με
με 
 είναι
είναι  , άρα το σύστημα είναι αδύνατο
, άρα το σύστημα είναι αδύνατο