 είναι πίνακες
είναι πίνακες  και ισχύουν οι σχέσεις
και ισχύουν οι σχέσεις  και
και  όπου
όπου  ο μηδενικός πίνακας
ο μηδενικός πίνακας 
τότε να αποδείξετε ότι είναι
 .
.β) Έστω
 πίνακες
πίνακες  και
και  ο μοναδιαίος πίνακας
ο μοναδιαίος πίνακας  .
. Αν ισχύει ότι
 τότε να αποδείξετε ότι ο
τότε να αποδείξετε ότι ο  είναι αντιστρέψιμος και ότι
είναι αντιστρέψιμος και ότι 
γ) Έστω
 πίνακες
πίνακες  όπου ο
όπου ο  είναι αντιστρέψιμος.
είναι αντιστρέψιμος. Να αποδείξετε ότι για κάθε
 θετικό ακέραιο ισχύει η σχέση
θετικό ακέραιο ισχύει η σχέση  .
.2. α) Να αποδείξετε ότι αν η συνάρτηση
 είναι συνεχής στο
είναι συνεχής στο ![\displaystyle{[\alpha ,\beta]} \displaystyle{[\alpha ,\beta]}](/forum/ext/geomar/texintegr/latexrender/pictures/52427afc2dcbdbb11264309a8f654c9a.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 
τότε υπάρχει
 τέτοιο ώστε να είναι
τέτοιο ώστε να είναι  .
.β) Θεωρούμε τη συνάρτηση
 με
με  όπου
όπου  είναι πραγματικοί αριθμοί
είναι πραγματικοί αριθμοί και ισχύει
 .
.Να αποδείξετε ότι υπάρχει
 τέτοιο ώστε η εφαπτομένη της γραφικής παράστασης της
τέτοιο ώστε η εφαπτομένη της γραφικής παράστασης της  στο σημείο
στο σημείο 
να είναι παράλληλη προς τον άξονα
 .
.3. α) Θεωρούμε κύκλο με κέντρο
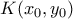 και ακτίνα
και ακτίνα  καθώς και σημείο
καθώς και σημείο  αυτού του κύκλου.
αυτού του κύκλου. Να αποδείξετε ότι η εφαπτομένη του κύκλου στο σημείο
 έχει εξίσωση
έχει εξίσωση  .
.β) Δίνονται η ευθεία
 με εξίσωση
με εξίσωση 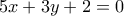 και ο κύκλος
και ο κύκλος  με εξίσωση
με εξίσωση  που τέμνονται στα σημεία
που τέμνονται στα σημεία  και
και  .
.i) Να αποδείξετε ότι για κάθε πραγματικό αριθμό
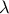 η εξίσωση
η εξίσωση  παριστάνει κύκλο
παριστάνει κύκλο ο οποίος περνάει από τα σημεία
 και
και  . Για ποια τιμή του
. Για ποια τιμή του 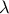 ο κύκλος αυτός περνάει από την αρχή των αξόνων;
ο κύκλος αυτός περνάει από την αρχή των αξόνων;ii) Να αποδείξετε ότι τα κέντρα των κύκλων του ερωτήματος (i) ανήκουν σε ευθεία
 της οποίας να βρείτε την εξίσωση.
της οποίας να βρείτε την εξίσωση.4. Δίνεται η συνάρτηση
 με
με 
α) Να βρείτε τις ασύμπτωτες της γραφικής παράστασης της συνάρτησης
β) Να υπολογίσετε το εμβαδόν
 του χωρίου που περικλείεται μεταξύ της γραφικής παράστασης της
του χωρίου που περικλείεται μεταξύ της γραφικής παράστασης της  της ευθείας
της ευθείας με εξίσωση
 και των ευθειών με εξισώσεις
και των ευθειών με εξισώσεις 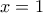 και
και  με
με  .
.γ) Να υπολογίσετε το όριο του εμβαδού
 του ανωτέρου χωρίου όταν το
του ανωτέρου χωρίου όταν το  \alpha}$ τείνει στο άπειρο.
\alpha}$ τείνει στο άπειρο.
 , όμοια
, όμοια
 και αφού
και αφού 

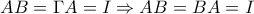 άρα ο
άρα ο  αντιστρέφεται με
αντιστρέφεται με 
 προφανώς η σχέση ισχύει
προφανώς η σχέση ισχύει δηλαδή
δηλαδή 
 είναι
είναι  και το ζητούμενο έπεται από τη μαθηματική επαγωγή.
και το ζητούμενο έπεται από τη μαθηματική επαγωγή. η οποία είναι:
η οποία είναι: Συνεχής στο διάστημα
Συνεχής στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ως πολυωνυμική,
ως πολυωνυμική, για τον ίδιο λόγο.
για τον ίδιο λόγο.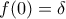 και
και 

 από όπου αποδεικνύεται το ζητούμενο.
από όπου αποδεικνύεται το ζητούμενο.