
β) Να δείξετε ότι το σύνολο
 εφοδιασμένο με την συνήθη πράξη
εφοδιασμένο με την συνήθη πράξη του πολλαπλασιασμού κλασμάτων στο
 είναι πολλαπλασιαστική ομάδα.
είναι πολλαπλασιαστική ομάδα.2. α) Να αποδείξετε ότι κάθε ακολουθία αύξουσα και φραγμένη άνω είναι συγκλίνουσα
β) Να βρείτε το όριο της ακολουθίας
 με
με  και
και  .
.3. α) Θεωρούμε συνάρτηση
 ορισμένη σε ένα διάστημα
ορισμένη σε ένα διάστημα  .
. Να αποδείξετε ότι αν η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και
και  τότε και
τότε και η συνάρτηση
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και είναι
και είναι ![\displaystyle{{{\left( \frac{1}{g} \right)}^{\prime }}({{x}_{0}})=-\frac{{g}'({{x}_{0}})}{{{\left[ g({{x}_{0}}) \right]}^{2}}}} \displaystyle{{{\left( \frac{1}{g} \right)}^{\prime }}({{x}_{0}})=-\frac{{g}'({{x}_{0}})}{{{\left[ g({{x}_{0}}) \right]}^{2}}}}](/forum/ext/geomar/texintegr/latexrender/pictures/eb6e784dd75485c91b94ae26384a8c5b.png) .
.β) Δίνεται η συνάρτηση
 με
με 
i) Να βρείτε τα διαστήματα μονοτονίας και τα ακρότατα της συνάρτησης .
ii) Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση
 της συνάρτησης
της συνάρτησης  τον άξονα
τον άξονα 
και τις ευθείες με εξισώσεις
 .
.4. α) i) Να δώσετε τον ορισμό της παραβολής.
ii) Δίνεται η παραβολή
 και η ευθεία με εξίσωση
και η ευθεία με εξίσωση  .
. Να αποδείξετε ότι η ευθεία και η παραβολή έχουν ένα διπλό κοινό σημείο αν και μόνο αν
 .
.β) Δίνεται η παραβολή με εξίσωση
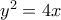 .
.i) Να βρείτε την εξίσωση της εφαπτομένης της παραβολής που είναι κάθετη στην ευθεία με εξίσωση
 .
.ii) Να βρείτε τις εξισώσεις των εφαπτόμενων της παραβολής τις οποίες φέρνουμε από το σημείο
 .
.
 και την ευθεία:
και την ευθεία: 
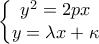 θα επιλύσουμε το μη γραμμικό αυτό σύστημα με την μέθοδο της αντικατάστασης, δηλαδή:
θα επιλύσουμε το μη γραμμικό αυτό σύστημα με την μέθοδο της αντικατάστασης, δηλαδή:
 παρατηρούμε ότι είναι τριώνυμο ως προς
παρατηρούμε ότι είναι τριώνυμο ως προς  και αφού θέλουμε το εν λόγω τριώνυμο να έχει διπλή λύση, τότε απαιτούμε:
και αφού θέλουμε το εν λόγω τριώνυμο να έχει διπλή λύση, τότε απαιτούμε: ![\Delta =0\Leftrightarrow \beta ^{2}-4\alpha \gamma =0\Leftrightarrow [2(\lambda \kappa -p)]^2-4\lambda ^{2}\kappa ^{2}=0\Leftrightarrow 4(\lambda^2 \kappa ^{2}-2\lambda \kappa p+p^{2})-4\lambda^2 \kappa ^{2}=0\Leftrightarrow 4p^{2}=8\lambda \kappa p\overset{p\neq 0}{\rightarrow}p=2\kappa \lambda \Delta =0\Leftrightarrow \beta ^{2}-4\alpha \gamma =0\Leftrightarrow [2(\lambda \kappa -p)]^2-4\lambda ^{2}\kappa ^{2}=0\Leftrightarrow 4(\lambda^2 \kappa ^{2}-2\lambda \kappa p+p^{2})-4\lambda^2 \kappa ^{2}=0\Leftrightarrow 4p^{2}=8\lambda \kappa p\overset{p\neq 0}{\rightarrow}p=2\kappa \lambda](/forum/ext/geomar/texintegr/latexrender/pictures/1aa88915e5795b3dc4d398e4e2fedc9c.png)
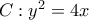 από όπου παίρνουμε:
από όπου παίρνουμε: 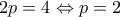

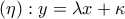 ζητούμενη και αφού
ζητούμενη και αφού 
 αν εφαρμόσουμε το προηγούμενο ερώτημα
αν εφαρμόσουμε το προηγούμενο ερώτημα 
 .
. το κοινό σημείο της ζητούμενης ευθείας με την κωνική. Από θεωρία γνωρίζουμε ότι όταν έχουμε το σημείο επαφής η εξίσωση εφαπτομένης δίνεται από τον τύπο:
το κοινό σημείο της ζητούμενης ευθείας με την κωνική. Από θεωρία γνωρίζουμε ότι όταν έχουμε το σημείο επαφής η εξίσωση εφαπτομένης δίνεται από τον τύπο: 
 .
. 


 Οπότε προκύπτουν δύο ευθείες που είναι οι ζητούμενες:
Οπότε προκύπτουν δύο ευθείες που είναι οι ζητούμενες: 
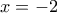 δεν αποτελεί λύση του προβλήματός μας.
δεν αποτελεί λύση του προβλήματός μας. με τύπο:
με τύπο: 
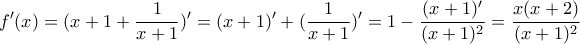 με την βοήθεια και του ερωτήματος Α, πάντα με
με την βοήθεια και του ερωτήματος Α, πάντα με  .
.
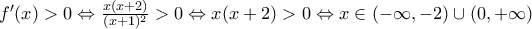

 και
και 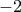 σημαίνει ότι τα σημεία αυτά είναι τοπικά ακρότατα σύμφωνα με το θεώρημα της πρώτης παραγώγου.
σημαίνει ότι τα σημεία αυτά είναι τοπικά ακρότατα σύμφωνα με το θεώρημα της πρώτης παραγώγου. ![\left ( -\infty,-2\right ]\cup \left [ 0,+\infty \right ) \left ( -\infty,-2\right ]\cup \left [ 0,+\infty \right )](/forum/ext/geomar/texintegr/latexrender/pictures/7110dbfc548424468db4e055072c3c9a.png) και γνησίως φθίνουσα στο:
και γνησίως φθίνουσα στο: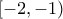 και
και![(-1,0] (-1,0]](/forum/ext/geomar/texintegr/latexrender/pictures/291752b00d4774efa8912eafde589cc4.png) . Οπότε, το σημείο
. Οπότε, το σημείο  είναι τοπικό μέγιστο και
είναι τοπικό μέγιστο και  είναι τοπικό ελάχιστο.
είναι τοπικό ελάχιστο.
![[2,5] [2,5]](/forum/ext/geomar/texintegr/latexrender/pictures/db5dc72ec1da78e609bf9f0ae1447688.png) αφού
αφού  συνεπώς είναι:
συνεπώς είναι:  στο
στο  .
. ):
):

 ,
,  ,
,
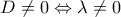 . Tότε το σύστημα (
. Tότε το σύστημα ( . Για να είναι δεκτή η λύση αυτή, πρέπει να επαληθεύει και την
. Για να είναι δεκτή η λύση αυτή, πρέπει να επαληθεύει και την 
 , (αφού είναι
, (αφού είναι  ).
).
 . Τότε το δοσμένο σύστημα είναι ισοδύναμο με την εξίσωση
. Τότε το δοσμένο σύστημα είναι ισοδύναμο με την εξίσωση  , η οποία έχει άπειρες
, η οποία έχει άπειρες  , με
, με 

 , διότι π.χ
, διότι π.χ  , (αφού
, (αφού 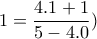 .
. είναι κλειστό ως προς την πράξη του πολλαπλασιασμού:
είναι κλειστό ως προς την πράξη του πολλαπλασιασμού: Τότε υπάρχουν ακέραιοι αριθμοί
Τότε υπάρχουν ακέραιοι αριθμοί  και
και  , ώστε:
, ώστε: και
και  . Άρα:
. Άρα: ,
, . Άρα
. Άρα 
 , υπάρχει
, υπάρχει  , τέτοιο ώστε
, τέτοιο ώστε 
 , ώστε
, ώστε 
 ,
, και αφού
και αφού  , έχουμε ότι
, έχουμε ότι 
 είναι αβελιανή ομάδα
είναι αβελιανή ομάδα και
και 
 προκύπτει:
προκύπτει: 
 . Επίσης ισχύει:
. Επίσης ισχύει:  .
. .
. Για
Για  έχω
έχω  που ισχύει.
που ισχύει. δηλαδή:
δηλαδή: 
 δηλαδή:
δηλαδή:  .
.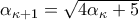

 που σημαίνει ότι η ακολουθία:
που σημαίνει ότι η ακολουθία:  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. , δηλαδή:
, δηλαδή: 
 που σημαίνει ότι η εν λόγω ακολουθία είναι φραγμένη άνω. Οπότε σύμφωνα με το α) ερώτημα του ζητήματος συγκλίνει.
που σημαίνει ότι η εν λόγω ακολουθία είναι φραγμένη άνω. Οπότε σύμφωνα με το α) ερώτημα του ζητήματος συγκλίνει. οπότε
οπότε 
 , Άρα
, Άρα  με
με 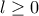 .
.  με λύσεις :
με λύσεις :  , αυτή που ικανοποιεί τον περιορισμό είναι:
, αυτή που ικανοποιεί τον περιορισμό είναι: 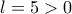 .
. που είναι και το ζητούμενο.
που είναι και το ζητούμενο. Το σημείο
Το σημείο  είναι κέντρο συμμετρίας της
είναι κέντρο συμμετρίας της  αν και μόνο αν:
αν και μόνο αν: είναι
είναι  και
και για κάθε
για κάθε  είναι κέντρο συμμετρίας της
είναι κέντρο συμμετρίας της  και
και  αφού:
αφού: και
και
 είναι
είναι 
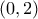 ως προς το
ως προς το 