Συγκεντρωμένες θα είναι στο Ευρετήριο Θεμάτων Πανελλαδικών Εξετάσεων
1. α) Αν
 ακολουθίες πραγματικών αριθμών με
ακολουθίες πραγματικών αριθμών με  να αποδειχθεί ότι
να αποδειχθεί ότι 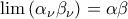 .
.β) Να βρεθεί το όριο της ακολουθίας
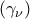 με
με ![{{\gamma }_{\nu }}=\sqrt[\nu ]{{{\nu }^{\nu +1}}}\left( \sqrt{{{\nu }^{2}}+1}-\nu \right) {{\gamma }_{\nu }}=\sqrt[\nu ]{{{\nu }^{\nu +1}}}\left( \sqrt{{{\nu }^{2}}+1}-\nu \right)](/forum/ext/geomar/texintegr/latexrender/pictures/923121cd3274de71de59b554b3f066a5.png)
2. Η συνάρτηση
 ορισμένη και συνεχής στο κλειστό διάστημα
ορισμένη και συνεχής στο κλειστό διάστημα ![[\alpha ,\beta ] [\alpha ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/13ac621dab037fd260a54755bb2382a3.png) έχει παράγωγο στο ανοικτό διάστημα
έχει παράγωγο στο ανοικτό διάστημα  και
και 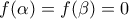 .
. Να αποδειχθεί :
α) Ότι για τη συνάρτηση
 όπου
όπου ![c\notin [\alpha ,\beta ] c\notin [\alpha ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/3ad513b03c7ae90705c08d0df4e3377d.png) υπάρχει
υπάρχει  τέτοιο ώστε
τέτοιο ώστε  .
.β) Αν
![c\notin [\alpha ,\beta ] c\notin [\alpha ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/3ad513b03c7ae90705c08d0df4e3377d.png) , ότι υπάρχει
, ότι υπάρχει  τέτοιο ώστε η εφαπτομένη στο σημείο
τέτοιο ώστε η εφαπτομένη στο σημείο  της γραμμής με εξίσωση
της γραμμής με εξίσωση  διέρχεται από το σημείο
διέρχεται από το σημείο  .
.3. α) Να αποδειχθεί ότι για κάθε
 ισχύει η σχέση
ισχύει η σχέση  .
.β) Έστω η συνάρτηση
 ορισμένη στο διάστημα
ορισμένη στο διάστημα  με
με  .
. Να αποδειχθεί ότι :
i) Η
 είναι συνεχής στο πεδίο ορισμού της
είναι συνεχής στο πεδίο ορισμού της ii) Είναι φθίνουσα στο διάστημα

iii)

4. Στο τετράεδρο
 να αποδειχθεί ότι :
να αποδειχθεί ότι :α) Αν
 και
και  τότε
τότε 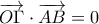
β) Αν
 και
και 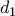 είναι η απόσταση των μέσων των ευθυγράμμων τμημάτων
είναι η απόσταση των μέσων των ευθυγράμμων τμημάτων  και
και  είναι η απόσταση των μέσων των ευθυγράμμων τμημάτων
είναι η απόσταση των μέσων των ευθυγράμμων τμημάτων  τότε
τότε  .
.Υ.Γ. Για να φαίνεται πιο ωραία η απάντηση της καλό είναι να συνοδεύεται από την εκφώνηση της.
Για να το κάνετε αυτό κάνετε παράθεση στην αρχική δημοσίευση
και από την παράθεση αυτή σβήνετε τις υπόλοιπες ασκήσεις, κατόπιν την λύνετε κανονικά .
edit
Διορθώθηκε ο παρονομαστής στην κλαδική συνάρτηση στο 3ο θέμα, σωστός ο Ωmega Man

![\displaystyle{\gamma _\nu =\nu \sqrt[\nu]{\nu}\frac{(\sqrt{\nu ^2 +1}-\nu )(\sqrt{\nu ^2 +1}+\nu )}{\sqrt{\nu ^2 +1}+\nu}=} \displaystyle{\gamma _\nu =\nu \sqrt[\nu]{\nu}\frac{(\sqrt{\nu ^2 +1}-\nu )(\sqrt{\nu ^2 +1}+\nu )}{\sqrt{\nu ^2 +1}+\nu}=}](/forum/ext/geomar/texintegr/latexrender/pictures/2337f4f8da53d08cffbc9d76e67911e3.png)
![\displaystyle{=\nu \sqrt[\nu]{\nu}\frac{1}{\nu \sqrt{1+\frac{1}{\nu}}+\nu}=\frac{\sqrt[\nu ]{\nu}}{\sqrt{1+\frac{1}{\nu}}+1}} \displaystyle{=\nu \sqrt[\nu]{\nu}\frac{1}{\nu \sqrt{1+\frac{1}{\nu}}+\nu}=\frac{\sqrt[\nu ]{\nu}}{\sqrt{1+\frac{1}{\nu}}+1}}](/forum/ext/geomar/texintegr/latexrender/pictures/d8a88b16cecb33707bb98934260f2a67.png)
![\displaystyle{lim \sqrt[\nu ]{\nu}=1} \displaystyle{lim \sqrt[\nu ]{\nu}=1}](/forum/ext/geomar/texintegr/latexrender/pictures/bdb09ca7c56ee8633718eb26576574ce.png) και
και 

 με το
με το  και διορθώθηκε μια αβλεψία στο τέλος
και διορθώθηκε μια αβλεψία στο τέλος , ισχύουν οι προϋποθέσεις του Θ. Rolle. Άρα υπάρχει
, ισχύουν οι προϋποθέσεις του Θ. Rolle. Άρα υπάρχει  ώστε να είναι
ώστε να είναι 
 . Άρα
. Άρα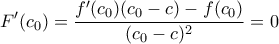 . Συνεπώς:
. Συνεπώς:  , (ΣΧΕΣΗ 1).
, (ΣΧΕΣΗ 1). που ζητάμε , είναι αυτό που βρήκαμε στην πρώτη ερώτηση.
που ζητάμε , είναι αυτό που βρήκαμε στην πρώτη ερώτηση.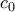 , είναι:
, είναι: . Πρέπει να δείξουμε ότι η ευθεία αυτή διέρχεται από το σημείο
. Πρέπει να δείξουμε ότι η ευθεία αυτή διέρχεται από το σημείο  , το οποίο είναι αληθές εξ αιτίας της (ΣΧΕΣΗΣ 1).
, το οποίο είναι αληθές εξ αιτίας της (ΣΧΕΣΗΣ 1). .
.  είναι προφανές ότι
είναι προφανές ότι  , για
, για  επαληθεύεται η ισότητα
επαληθεύεται η ισότητα  και μένει να δούμε τι γίνεται για
και μένει να δούμε τι γίνεται για  .
. και εφόσον η h είναι γνησίως φθίνουσα και
και εφόσον η h είναι γνησίως φθίνουσα και  , έπεται ότι
, έπεται ότι  .
. για κάθε
για κάθε  .
. , άρα στο
, άρα στο  είναι συνεχής.
είναι συνεχής. , άρα είναι συνεχής στο
, άρα είναι συνεχής στο  .
. , αφού ο παρονομαστής είναι πάντα θετικός αρκεί να μελετήσουμε τον αριθμητή.
, αφού ο παρονομαστής είναι πάντα θετικός αρκεί να μελετήσουμε τον αριθμητή. , άρα αφού κ γνησίως αύξουσα και
, άρα αφού κ γνησίως αύξουσα και 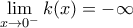 και
και  , έπεται ότι
, έπεται ότι  , άρα
, άρα  για κάθε
για κάθε 
![\displaystyle{\gamma _n =n\sqrt[n]{n}\frac{(\sqrt{n^2 +1}-n)(\sqrt{n^2 +1}+n)}{\sqrt{n^2 +1}+n}=} \displaystyle{\gamma _n =n\sqrt[n]{n}\frac{(\sqrt{n^2 +1}-n)(\sqrt{n^2 +1}+n)}{\sqrt{n^2 +1}+n}=}](/forum/ext/geomar/texintegr/latexrender/pictures/e3fbb23c7e47550c3ba4809deef997ae.png)
![\displaystyle{=n\sqrt[n]{n}\frac{1}{n\sqrt{1+\frac{1}{n}}+n}=\frac{\sqrt[n]{n}}{\sqrt{1+\frac{1}{n}}+1}} \displaystyle{=n\sqrt[n]{n}\frac{1}{n\sqrt{1+\frac{1}{n}}+n}=\frac{\sqrt[n]{n}}{\sqrt{1+\frac{1}{n}}+1}}](/forum/ext/geomar/texintegr/latexrender/pictures/67e42b56436405de66884523d8f8d19a.png)
![\displaystyle{lim \sqrt[n]{n}=1} \displaystyle{lim \sqrt[n]{n}=1}](/forum/ext/geomar/texintegr/latexrender/pictures/dc7962ac64f59e08a45e67f573d3d18c.png) και
και 

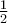 και όχι με τη ρίζα?
και όχι με τη ρίζα? . Θα κάνω την διόρθωση
. Θα κάνω την διόρθωση της συνάρτησης
της συνάρτησης ![f(x)=\sqrt[x]{{{x}^{x+1}}}\left( \sqrt{{{x}^{2}}+1}-x \right) f(x)=\sqrt[x]{{{x}^{x+1}}}\left( \sqrt{{{x}^{2}}+1}-x \right)](/forum/ext/geomar/texintegr/latexrender/pictures/cb9355ce477b5d3d09f027101fd38f92.png)
![f(x)=\sqrt[x]{{{x}^{x+1}}}\left( \sqrt{{{x}^{2}}+1}-x \right)=\sqrt[x]{{{x}^{x}}}\cdot \sqrt{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)= f(x)=\sqrt[x]{{{x}^{x+1}}}\left( \sqrt{{{x}^{2}}+1}-x \right)=\sqrt[x]{{{x}^{x}}}\cdot \sqrt{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=](/forum/ext/geomar/texintegr/latexrender/pictures/2e41d1ddd1d93d26d7e220363421f68f.png)
![\displaystyle{=x\cdot \sqrt[x]{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=x\cdot \sqrt[x]{x}\cdot \frac{\left( \sqrt{{{x}^{2}}+1}-x \right)\cdot \left( \sqrt{{{x}^{2}}+1}+x \right)}{\sqrt{{{x}^{2}}+1}+x}=} \displaystyle{=x\cdot \sqrt[x]{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=x\cdot \sqrt[x]{x}\cdot \frac{\left( \sqrt{{{x}^{2}}+1}-x \right)\cdot \left( \sqrt{{{x}^{2}}+1}+x \right)}{\sqrt{{{x}^{2}}+1}+x}=}](/forum/ext/geomar/texintegr/latexrender/pictures/3e75fdb41f2c029637cb45ddb8ad3488.png)
![\displaystyle{=x\cdot \sqrt[x]{x}\cdot \frac{1}{\left| x \right|\sqrt{1+\frac{1}{{{x}^{2}}}}+x}\overset{x\to +\infty }{\mathop{\text{ }=}}\,x\cdot \sqrt[x]{x}\cdot \frac{1}{x\sqrt{1+\frac{1}{{{x}^{2}}}}+x}=} \displaystyle{=x\cdot \sqrt[x]{x}\cdot \frac{1}{\left| x \right|\sqrt{1+\frac{1}{{{x}^{2}}}}+x}\overset{x\to +\infty }{\mathop{\text{ }=}}\,x\cdot \sqrt[x]{x}\cdot \frac{1}{x\sqrt{1+\frac{1}{{{x}^{2}}}}+x}=}](/forum/ext/geomar/texintegr/latexrender/pictures/840cdd084f5c6a045364f4fc44f14f6f.png)
![\displaystyle{f(x)=\sqrt[x]{{{x}^{x+1}}}\left( \sqrt{{{x}^{2}}+1}-x \right)=\sqrt[x]{{{x}^{x}}}\cdot \sqrt{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=x\cdot \sqrt[x]{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=} \displaystyle{f(x)=\sqrt[x]{{{x}^{x+1}}}\left( \sqrt{{{x}^{2}}+1}-x \right)=\sqrt[x]{{{x}^{x}}}\cdot \sqrt{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=x\cdot \sqrt[x]{x}\cdot \left( \sqrt{{{x}^{2}}+1}-x \right)=}](/forum/ext/geomar/texintegr/latexrender/pictures/35c6f13619aa43eb53e387574b7d082e.png)

![\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\sqrt[x]{x}=\underset{x\to +\infty }{\mathop{\lim }}\,{{\left( x \right)}^{\frac{1}{x}}}=\underset{x\to +\infty }{\mathop{\lim }}\,{{e}^{\ell n{{x}^{\frac{1}{x}}}}}=\underset{x\to +\infty }{\mathop{\lim }}\,{{e}^{\frac{1}{x}\cdot \ell nx}}} \displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\sqrt[x]{x}=\underset{x\to +\infty }{\mathop{\lim }}\,{{\left( x \right)}^{\frac{1}{x}}}=\underset{x\to +\infty }{\mathop{\lim }}\,{{e}^{\ell n{{x}^{\frac{1}{x}}}}}=\underset{x\to +\infty }{\mathop{\lim }}\,{{e}^{\frac{1}{x}\cdot \ell nx}}}](/forum/ext/geomar/texintegr/latexrender/pictures/56e1b5d7cfddd134fe99de2005cc5025.png)
 και
και 

![\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{\sqrt[x]{x}}{\sqrt{1+\frac{1}{{{x}^{2}}}}+1}=\frac{1}{2} \underset{x\to +\infty }{\mathop{\lim }}\,f(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{\sqrt[x]{x}}{\sqrt{1+\frac{1}{{{x}^{2}}}}+1}=\frac{1}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/9d349e69f39bd65b63eaf302a90c6687.png)

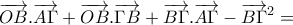
 =
=
 . Επίσης:
. Επίσης:
 είναι τα μέσα των
είναι τα μέσα των 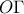 και
και  αντιστοίχως, έχουμε:
αντιστοίχως, έχουμε:
 , (ΣΧΕΣΗ 1)
, (ΣΧΕΣΗ 1) , (ΣΧΕΣΗ 2)
, (ΣΧΕΣΗ 2)


