ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Συντονιστής: Μιχάλης Νάννος
ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Τα κόκκινα είναι τα νέα θέματα και τα μεύρα παλιά που συμπληρώθηκαν οι εκφωνήσεις τους
01. ΘΕΜΑ 4-2789
02. ΘΕΜΑ 4-2809
03. ΘΕΜΑ 4-3702
04. ΘΕΜΑ 4-3703
05. ΘΕΜΑ 4-3711
06. ΘΕΜΑ 4-3731
07. ΘΕΜΑ 4-3767
08. ΘΕΜΑ 4-3803
09. ΘΕΜΑ 4-3813
10. ΘΕΜΑ 4-4555
11. ΘΕΜΑ 4-4579
12. ΘΕΜΑ 4-4614
13. ΘΕΜΑ 4-4619
14. ΘΕΜΑ 4-4652
15. ΘΕΜΑ 4-4653
16. ΘΕΜΑ 4-4741
17. ΘΕΜΑ 4-4753
18. ΘΕΜΑ 4-4762
19. ΘΕΜΑ 4-4778
20. ΘΕΜΑ 4-4786
21. ΘΕΜΑ 4-4794
22. ΘΕΜΑ 4-4798
23. ΘΕΜΑ 4-4804
24. ΘΕΜΑ 4-4806
25. ΘΕΜΑ 4-4808
26. ΘΕΜΑ 4-6876
27. ΘΕΜΑ 4-13527
01. ΘΕΜΑ 4-2789
02. ΘΕΜΑ 4-2809
03. ΘΕΜΑ 4-3702
04. ΘΕΜΑ 4-3703
05. ΘΕΜΑ 4-3711
06. ΘΕΜΑ 4-3731
07. ΘΕΜΑ 4-3767
08. ΘΕΜΑ 4-3803
09. ΘΕΜΑ 4-3813
10. ΘΕΜΑ 4-4555
11. ΘΕΜΑ 4-4579
12. ΘΕΜΑ 4-4614
13. ΘΕΜΑ 4-4619
14. ΘΕΜΑ 4-4652
15. ΘΕΜΑ 4-4653
16. ΘΕΜΑ 4-4741
17. ΘΕΜΑ 4-4753
18. ΘΕΜΑ 4-4762
19. ΘΕΜΑ 4-4778
20. ΘΕΜΑ 4-4786
21. ΘΕΜΑ 4-4794
22. ΘΕΜΑ 4-4798
23. ΘΕΜΑ 4-4804
24. ΘΕΜΑ 4-4806
25. ΘΕΜΑ 4-4808
26. ΘΕΜΑ 4-6876
27. ΘΕΜΑ 4-13527
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Καλημέρα Χρήστο
Τα νέα αυτά θέματα, όταν λυθούν, σε ποιο φάκελο μπορούμε να τα αναρτήσουμε;
Τα νέα αυτά θέματα, όταν λυθούν, σε ποιο φάκελο μπορούμε να τα αναρτήσουμε;
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Γιώργο βάλτε τα σε αυτό το post με times New roman 12 και θα τα αποδελτιώσω σιγά σιγά
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
01. Άσκηση 4-2789
Δίνεται τρίγωνο στο οποίο η εξωτερική του γωνία
στο οποίο η εξωτερική του γωνία  είναι διπλάσια της εσωτερικής του γωνίας
είναι διπλάσια της εσωτερικής του γωνίας  . Από την κορυφή
. Από την κορυφή  διέρχεται ημιευθεία
διέρχεται ημιευθεία  στο ημιεπίπεδο
στο ημιεπίπεδο  . Στην ημιευθεία
. Στην ημιευθεία  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε 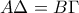 . Να αποδείξετε ότι:
. Να αποδείξετε ότι:
α) Η διέρχεται από το μέσο του τμήματος
διέρχεται από το μέσο του τμήματος  . (Μονάδες
. (Μονάδες  )
)
β) Η είναι διχοτόμος της
είναι διχοτόμος της 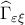 . (Μονάδες
. (Μονάδες  )
)
γ) Το τρίγωνο είναι ισοσκελές. (Μονάδες
είναι ισοσκελές. (Μονάδες  )
)
Λύση:
α) Επειδή , το τετράπλευρο
, το τετράπλευρο  είναι παραλληλόγραμμο, οπότε οι διαγώνιες του διχοτομούνται και κατά συνέπεια η
είναι παραλληλόγραμμο, οπότε οι διαγώνιες του διχοτομούνται και κατά συνέπεια η  διέρχεται από το μέσο του τμήματος
διέρχεται από το μέσο του τμήματος  .
.
β) , οπότε
, οπότε  . Αλλά
. Αλλά  , άρα η
, άρα η  είναι διχοτόμος της
είναι διχοτόμος της 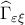 .
.
γ)

Επομένως το τρίγωνο είναι ισοσκελές.
είναι ισοσκελές.
Δίνεται τρίγωνο
 στο οποίο η εξωτερική του γωνία
στο οποίο η εξωτερική του γωνία  είναι διπλάσια της εσωτερικής του γωνίας
είναι διπλάσια της εσωτερικής του γωνίας  . Από την κορυφή
. Από την κορυφή  διέρχεται ημιευθεία
διέρχεται ημιευθεία  στο ημιεπίπεδο
στο ημιεπίπεδο  . Στην ημιευθεία
. Στην ημιευθεία  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε 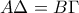 . Να αποδείξετε ότι:
. Να αποδείξετε ότι:α) Η
 διέρχεται από το μέσο του τμήματος
διέρχεται από το μέσο του τμήματος  . (Μονάδες
. (Μονάδες  )
)β) Η
 είναι διχοτόμος της
είναι διχοτόμος της 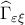 . (Μονάδες
. (Μονάδες  )
)γ) Το τρίγωνο
 είναι ισοσκελές. (Μονάδες
είναι ισοσκελές. (Μονάδες  )
)Λύση:
α) Επειδή
 , το τετράπλευρο
, το τετράπλευρο  είναι παραλληλόγραμμο, οπότε οι διαγώνιες του διχοτομούνται και κατά συνέπεια η
είναι παραλληλόγραμμο, οπότε οι διαγώνιες του διχοτομούνται και κατά συνέπεια η  διέρχεται από το μέσο του τμήματος
διέρχεται από το μέσο του τμήματος  .
.β)
 , οπότε
, οπότε  . Αλλά
. Αλλά  , άρα η
, άρα η  είναι διχοτόμος της
είναι διχοτόμος της 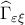 .
.γ)


Επομένως το τρίγωνο
 είναι ισοσκελές.
είναι ισοσκελές.- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
GI_A_GEO_4_2809
Δίνεται ισόπλευρο τρίγωνο και τα ύψη του
και τα ύψη του  και
και  , τα οποία τέμνονται στο
, τα οποία τέμνονται στο  . Αν τα σημεία
. Αν τα σημεία 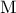 και
και  είναι τα μέσα των
είναι τα μέσα των  και
και  αντίστοιχα, να αποδείξετε ότι:
αντίστοιχα, να αποδείξετε ότι:
α) Το τρίγωνο είναι ισοσκελές (Μονάδες 5)
είναι ισοσκελές (Μονάδες 5)
β) Τα τρίγωνα και
και  είναι ίσα (Μονάδες 5)
είναι ίσα (Μονάδες 5)
γ) Το προεκτεινόμενο διέρχεται από το μέσο της πλευράς
προεκτεινόμενο διέρχεται από το μέσο της πλευράς  . (Μονάδες 5)
. (Μονάδες 5)
δ) Το τετράπλευρο είναι ορθογώνιο παραλληλόγραμμο. (Μονάδες 10)
είναι ορθογώνιο παραλληλόγραμμο. (Μονάδες 10)
α) Αφού το είναι ισόπλευρο, τα ύψη του είναι και διάμεσοι και διχοτόμοι, άρα
είναι ισόπλευρο, τα ύψη του είναι και διάμεσοι και διχοτόμοι, άρα  άρα το
άρα το  είναι ισοσκελές με
είναι ισοσκελές με  .
.
β) Τα τρίγωνα έχουν τις
έχουν τις  ίσες, όπως αποδείξαμε,
ίσες, όπως αποδείξαμε,  , ως κατακορυφήν γωνίες και
, ως κατακορυφήν γωνίες και  , αφού είναι
, αφού είναι 
Από το κριτήριο Γ-Π-Γ προκύπτει ότι είναι ίσα.
γ) Το είναι ορθόκεντρο του
είναι ορθόκεντρο του  , οπότε το
, οπότε το  βρίσκεται επί του ύψους του, το οποίο είναι και διάμεσός του, άρα το
βρίσκεται επί του ύψους του, το οποίο είναι και διάμεσός του, άρα το  προεκτεινόμενο διέρχεται από το μέσο της πλευράς ΒΓ.
προεκτεινόμενο διέρχεται από το μέσο της πλευράς ΒΓ.
δ) Αφού διάμεσοι, τα
διάμεσοι, τα  είναι μέσα των
είναι μέσα των  αντίστοιχα, οπότε είναι
αντίστοιχα, οπότε είναι 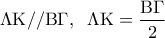
Ομοίως, αφού τα είναι μέσα των
είναι μέσα των  είναι και
είναι και  , οπότε το
, οπότε το  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.
Στο τα
τα  είναι μέσα των
είναι μέσα των  , οπότε είναι
, οπότε είναι  , άρα το
, άρα το  είναι ορθογώνιο παραλληλόγραμμο.
είναι ορθογώνιο παραλληλόγραμμο.
Δίνεται ισόπλευρο τρίγωνο
 και τα ύψη του
και τα ύψη του  και
και  , τα οποία τέμνονται στο
, τα οποία τέμνονται στο  . Αν τα σημεία
. Αν τα σημεία 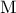 και
και  είναι τα μέσα των
είναι τα μέσα των  και
και  αντίστοιχα, να αποδείξετε ότι:
αντίστοιχα, να αποδείξετε ότι: α) Το τρίγωνο
 είναι ισοσκελές (Μονάδες 5)
είναι ισοσκελές (Μονάδες 5) β) Τα τρίγωνα
 και
και  είναι ίσα (Μονάδες 5)
είναι ίσα (Μονάδες 5) γ) Το
 προεκτεινόμενο διέρχεται από το μέσο της πλευράς
προεκτεινόμενο διέρχεται από το μέσο της πλευράς  . (Μονάδες 5)
. (Μονάδες 5) δ) Το τετράπλευρο
 είναι ορθογώνιο παραλληλόγραμμο. (Μονάδες 10)
είναι ορθογώνιο παραλληλόγραμμο. (Μονάδες 10) α) Αφού το
 είναι ισόπλευρο, τα ύψη του είναι και διάμεσοι και διχοτόμοι, άρα
είναι ισόπλευρο, τα ύψη του είναι και διάμεσοι και διχοτόμοι, άρα  άρα το
άρα το  είναι ισοσκελές με
είναι ισοσκελές με  .
.β) Τα τρίγωνα
 έχουν τις
έχουν τις  ίσες, όπως αποδείξαμε,
ίσες, όπως αποδείξαμε,  , ως κατακορυφήν γωνίες και
, ως κατακορυφήν γωνίες και  , αφού είναι
, αφού είναι 
Από το κριτήριο Γ-Π-Γ προκύπτει ότι είναι ίσα.
γ) Το
 είναι ορθόκεντρο του
είναι ορθόκεντρο του  , οπότε το
, οπότε το  βρίσκεται επί του ύψους του, το οποίο είναι και διάμεσός του, άρα το
βρίσκεται επί του ύψους του, το οποίο είναι και διάμεσός του, άρα το  προεκτεινόμενο διέρχεται από το μέσο της πλευράς ΒΓ.
προεκτεινόμενο διέρχεται από το μέσο της πλευράς ΒΓ.δ) Αφού
 διάμεσοι, τα
διάμεσοι, τα  είναι μέσα των
είναι μέσα των  αντίστοιχα, οπότε είναι
αντίστοιχα, οπότε είναι 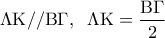
Ομοίως, αφού τα
 είναι μέσα των
είναι μέσα των  είναι και
είναι και  , οπότε το
, οπότε το  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.Στο
 τα
τα  είναι μέσα των
είναι μέσα των  , οπότε είναι
, οπότε είναι  , άρα το
, άρα το  είναι ορθογώνιο παραλληλόγραμμο.
είναι ορθογώνιο παραλληλόγραμμο.- Συνημμένα
-
- Λύση GI_A_GEO_4_2809.doc
- (107.5 KiB) Μεταφορτώθηκε 147 φορές
τελευταία επεξεργασία από Γιώργος Ρίζος σε Τετ Οκτ 29, 2014 9:05 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
03. Άσκηση 4-3702
Έστω ότι και
και  είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  και
και  παραλληλογράμμου Α
παραλληλογράμμου Α  αντίστοιχα.
αντίστοιχα.
Αν για το παραλληλόγραμμο ΑΒΓΔ επιπλέον ισχύουν και γωνία
και γωνία  αμβλεία , να εξετάσετε αν είναι αληθείς οι ακόλουθοι ισχυρισμοί:
αμβλεία , να εξετάσετε αν είναι αληθείς οι ακόλουθοι ισχυρισμοί:
Ισχυρισμός 1: Το τετράπλευρο είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.
Ισχυρισμός 2: Τα τρίγωνα και
και  είναι ίσα.
είναι ίσα.
Ισχυρισμός 3: Τα τρίγωνα και
και  είναι ισοσκελή.
είναι ισοσκελή.
α) Στην περίπτωση που θεωρείτε ότι κάποιος ισχυρισμός είναι αληθής να τον
αποδείξετε. (Μονάδες 16)
β) Στην περίπτωση που κάποιος ισχυρισμός δεν είναι αληθής, να βρείτε τη σχέση
των διαδοχικών πλευρών του παραλληλογράμμου ώστε να είναι αληθής. Να
αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
Λύση
α) Ο ισχυρισμός 1, δηλαδή ότι το είναι παραλληλόγραμμο ισχύει αφού είναι
είναι παραλληλόγραμμο ισχύει αφού είναι  ως μισά των ίσων και παραλλήλων τμημάτων
ως μισά των ίσων και παραλλήλων τμημάτων 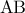 και
και  .
.
Ο ισχυρισμός 2 , δηλαδή ότι τα τρίγωνα και
και  είναι ίσα ισχύει αφού έχουν:
είναι ίσα ισχύει αφού έχουν:
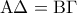 ως απέναντι πλευρές παραλληλογράμμου,
ως απέναντι πλευρές παραλληλογράμμου,
 ως απέναντι γωνίες παραλληλογράμμου και
ως απέναντι γωνίες παραλληλογράμμου και
 ως μισά των ίσων πλευρών
ως μισά των ίσων πλευρών 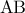 και
και  .
.
Ο ισχυρισμός 3 δεν είναι αληθής γενικά.
β) Για να ισχύει ο ισχυρισμός 3 πρέπει να ισχύει
Έστω ότι
 και
και  είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  και
και  παραλληλογράμμου Α
παραλληλογράμμου Α  αντίστοιχα.
αντίστοιχα. Αν για το παραλληλόγραμμο ΑΒΓΔ επιπλέον ισχύουν
 και γωνία
και γωνία  αμβλεία , να εξετάσετε αν είναι αληθείς οι ακόλουθοι ισχυρισμοί:
αμβλεία , να εξετάσετε αν είναι αληθείς οι ακόλουθοι ισχυρισμοί:Ισχυρισμός 1: Το τετράπλευρο
 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.Ισχυρισμός 2: Τα τρίγωνα
 και
και  είναι ίσα.
είναι ίσα. Ισχυρισμός 3: Τα τρίγωνα
 και
και  είναι ισοσκελή.
είναι ισοσκελή. α) Στην περίπτωση που θεωρείτε ότι κάποιος ισχυρισμός είναι αληθής να τον
αποδείξετε. (Μονάδες 16)
β) Στην περίπτωση που κάποιος ισχυρισμός δεν είναι αληθής, να βρείτε τη σχέση
των διαδοχικών πλευρών του παραλληλογράμμου ώστε να είναι αληθής. Να
αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
Λύση
α) Ο ισχυρισμός 1, δηλαδή ότι το
 είναι παραλληλόγραμμο ισχύει αφού είναι
είναι παραλληλόγραμμο ισχύει αφού είναι  ως μισά των ίσων και παραλλήλων τμημάτων
ως μισά των ίσων και παραλλήλων τμημάτων 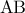 και
και  .
.Ο ισχυρισμός 2 , δηλαδή ότι τα τρίγωνα
 και
και  είναι ίσα ισχύει αφού έχουν:
είναι ίσα ισχύει αφού έχουν: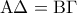 ως απέναντι πλευρές παραλληλογράμμου,
ως απέναντι πλευρές παραλληλογράμμου, ως απέναντι γωνίες παραλληλογράμμου και
ως απέναντι γωνίες παραλληλογράμμου και  ως μισά των ίσων πλευρών
ως μισά των ίσων πλευρών 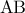 και
και  .
.Ο ισχυρισμός 3 δεν είναι αληθής γενικά.
β) Για να ισχύει ο ισχυρισμός 3 πρέπει να ισχύει

- Συνημμένα
-
- 3702.doc
- (81.5 KiB) Μεταφορτώθηκε 134 φορές
-
- 3702.png (14.67 KiB) Προβλήθηκε 7535 φορές
Ηλίας Καμπελής
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
04. Άσκηση 4-3703
Δίνεται τρίγωνο . Προεκτείνουμε το ύψος του
. Προεκτείνουμε το ύψος του  κατά τμήμα
κατά τμήμα  και τη
και τη
διάμεσό του κατά τμήμα
κατά τμήμα 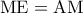 .
.
Να αποδείξετε ότι:
α)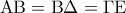 (Μονάδες 8)
(Μονάδες 8)
β) (Μονάδες 8)
(Μονάδες 8)
γ) Το τετράπλευρο είναι ισοσκελές τραπέζιο. (Μονάδες 9)
είναι ισοσκελές τραπέζιο. (Μονάδες 9)
Λύση
α) Το τρίγωνο είναι ισοσκελές αφού το
είναι ισοσκελές αφού το  είναι ύψος και διάμεσος, έτσι
είναι ύψος και διάμεσος, έτσι 
Τα τρίγωνα και
και  είναι ίσα αφού έχουν:
είναι ίσα αφού έχουν:
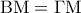 αφού το
αφού το  είναι μέσο της
είναι μέσο της 
 από υπόθεση και
από υπόθεση και
 ως κατακορυφήν.
ως κατακορυφήν.
Έτσι και
και 
Από
β) Στο ισοσκελές τρίγωνο το
το  είναι και διχοτόμος, έτσι
είναι και διχοτόμος, έτσι 
Από
γ) Σημείωση: Αυτό το ερώτημα νομίζω έχει πρόβλημα.
i. Αν είναι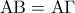 τα σημεία
τα σημεία  ταυτίζονται οπότε δεν υφίσταται τετράπλευρο
ταυτίζονται οπότε δεν υφίσταται τετράπλευρο  .
.
ii. Αν το
το  είναι ορθογώνιο.
είναι ορθογώνιο.
Σε περίπτωση που δεν ισχύουν τα παραπάνω, με το δοσμένο σχήμα δηλαδή, είναι:
Στο τρίγωνο το τμήμα
το τμήμα  ενώνει τα μέσα των πλευρών του
ενώνει τα μέσα των πλευρών του  αντίστοιχα, έτσι
αντίστοιχα, έτσι 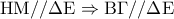 .
.
 δηλαδή οι
δηλαδή οι 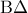 και
και  τέμνονται οπότε το
τέμνονται οπότε το  είναι ισοσκελές τραπέζιο αφού έχει και
είναι ισοσκελές τραπέζιο αφού έχει και 
Δίνεται τρίγωνο
 . Προεκτείνουμε το ύψος του
. Προεκτείνουμε το ύψος του  κατά τμήμα
κατά τμήμα  και τη
και τηδιάμεσό του
 κατά τμήμα
κατά τμήμα 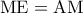 .
. Να αποδείξετε ότι:
α)
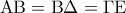 (Μονάδες 8)
(Μονάδες 8)β)
 (Μονάδες 8)
(Μονάδες 8)γ) Το τετράπλευρο
 είναι ισοσκελές τραπέζιο. (Μονάδες 9)
είναι ισοσκελές τραπέζιο. (Μονάδες 9)Λύση
α) Το τρίγωνο
 είναι ισοσκελές αφού το
είναι ισοσκελές αφού το  είναι ύψος και διάμεσος, έτσι
είναι ύψος και διάμεσος, έτσι 
Τα τρίγωνα
 και
και  είναι ίσα αφού έχουν:
είναι ίσα αφού έχουν: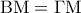 αφού το
αφού το  είναι μέσο της
είναι μέσο της 
 από υπόθεση και
από υπόθεση και  ως κατακορυφήν.
ως κατακορυφήν.Έτσι
 και
και 
Από

β) Στο ισοσκελές τρίγωνο
 το
το  είναι και διχοτόμος, έτσι
είναι και διχοτόμος, έτσι 
Από

γ) Σημείωση: Αυτό το ερώτημα νομίζω έχει πρόβλημα.
i. Αν είναι
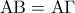 τα σημεία
τα σημεία  ταυτίζονται οπότε δεν υφίσταται τετράπλευρο
ταυτίζονται οπότε δεν υφίσταται τετράπλευρο  .
.ii. Αν
 το
το  είναι ορθογώνιο.
είναι ορθογώνιο.Σε περίπτωση που δεν ισχύουν τα παραπάνω, με το δοσμένο σχήμα δηλαδή, είναι:
Στο τρίγωνο
 το τμήμα
το τμήμα  ενώνει τα μέσα των πλευρών του
ενώνει τα μέσα των πλευρών του  αντίστοιχα, έτσι
αντίστοιχα, έτσι 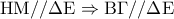 .
. δηλαδή οι
δηλαδή οι 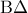 και
και  τέμνονται οπότε το
τέμνονται οπότε το  είναι ισοσκελές τραπέζιο αφού έχει και
είναι ισοσκελές τραπέζιο αφού έχει και 
- Συνημμένα
-
- 3703.doc
- (114.5 KiB) Μεταφορτώθηκε 129 φορές
-
- 3703.png (13.53 KiB) Προβλήθηκε 7495 φορές
Ηλίας Καμπελής
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
GI_A_GEO_4_3731
Δίνεται κύκλος και σημείο
και σημείο  εξωτερικό του. Από το
εξωτερικό του. Από το  φέρουμε τα εφαπτόμενα τμήματα
φέρουμε τα εφαπτόμενα τμήματα  και
και  του κύκλου και έστω ότι το σημείο
του κύκλου και έστω ότι το σημείο  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς την ευθεία
ως προς την ευθεία  .
.
α) Να αποδείξετε ότι το τετράπλευρο είναι εγγράψιμο σε κύκλο. (Μονάδες 7)
είναι εγγράψιμο σε κύκλο. (Μονάδες 7)
β) Να προσδιορίσετε το κέντρο του περιγγεγραμμένου κύκλου του τετραπλεύρου
του περιγγεγραμμένου κύκλου του τετραπλεύρου  και να αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
και να αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
γ) Να αποδείξετε ότι . (Μονάδες 9)
. (Μονάδες 9)
α) Τα είναι εφαπτόμενα τμήματα στον κύκλο, άρα είναι κάθετα στις ακτίνες
είναι εφαπτόμενα τμήματα στον κύκλο, άρα είναι κάθετα στις ακτίνες  αντίστοιχα, οπότε
αντίστοιχα, οπότε  , άρα το
, άρα το  είναι εγγράψιμο τετράπλευρο σε κύκλο αφού έχει δύο απέναντι γωνίες παραπληρωματικές.
είναι εγγράψιμο τετράπλευρο σε κύκλο αφού έχει δύο απέναντι γωνίες παραπληρωματικές.
β) Φέρνουμε τη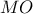 . Αφού είναι
. Αφού είναι  , η
, η 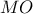 είναι διάμετρος του περιγεγραμμένου κύκλου του
είναι διάμετρος του περιγεγραμμένου κύκλου του  , οπότε το κέντρο
, οπότε το κέντρο  του κύκλου είναι το μέσο του
του κύκλου είναι το μέσο του 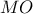 .
.
γ) Το είναι το μέσο του
είναι το μέσο του  και το
και το  είναι το μέσο του
είναι το μέσο του 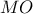 , οπότε στο τρίγωνο
, οπότε στο τρίγωνο  είναι
είναι 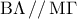 .
.
Χρήστο, παράβλεψα την 4-3711, αφού θέλει απλώς συμπλήρωση, για να μην την ξαναγράψω από την αρχή. Αν θες, ανάρτησε (σε word) όσες θέλουν απλώς συμπλήρωση για να τις επιμεληθούμε.
Δίνεται κύκλος
 και σημείο
και σημείο  εξωτερικό του. Από το
εξωτερικό του. Από το  φέρουμε τα εφαπτόμενα τμήματα
φέρουμε τα εφαπτόμενα τμήματα  και
και  του κύκλου και έστω ότι το σημείο
του κύκλου και έστω ότι το σημείο  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς την ευθεία
ως προς την ευθεία  .
. α) Να αποδείξετε ότι το τετράπλευρο
 είναι εγγράψιμο σε κύκλο. (Μονάδες 7)
είναι εγγράψιμο σε κύκλο. (Μονάδες 7) β) Να προσδιορίσετε το κέντρο
 του περιγγεγραμμένου κύκλου του τετραπλεύρου
του περιγγεγραμμένου κύκλου του τετραπλεύρου  και να αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
και να αιτιολογήσετε την απάντησή σας. (Μονάδες 9) γ) Να αποδείξετε ότι
 . (Μονάδες 9)
. (Μονάδες 9) α) Τα
 είναι εφαπτόμενα τμήματα στον κύκλο, άρα είναι κάθετα στις ακτίνες
είναι εφαπτόμενα τμήματα στον κύκλο, άρα είναι κάθετα στις ακτίνες  αντίστοιχα, οπότε
αντίστοιχα, οπότε  , άρα το
, άρα το  είναι εγγράψιμο τετράπλευρο σε κύκλο αφού έχει δύο απέναντι γωνίες παραπληρωματικές.
είναι εγγράψιμο τετράπλευρο σε κύκλο αφού έχει δύο απέναντι γωνίες παραπληρωματικές.β) Φέρνουμε τη
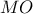 . Αφού είναι
. Αφού είναι  , η
, η 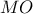 είναι διάμετρος του περιγεγραμμένου κύκλου του
είναι διάμετρος του περιγεγραμμένου κύκλου του  , οπότε το κέντρο
, οπότε το κέντρο  του κύκλου είναι το μέσο του
του κύκλου είναι το μέσο του 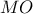 .
. γ) Το
 είναι το μέσο του
είναι το μέσο του  και το
και το  είναι το μέσο του
είναι το μέσο του 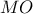 , οπότε στο τρίγωνο
, οπότε στο τρίγωνο  είναι
είναι 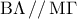 .
.Χρήστο, παράβλεψα την 4-3711, αφού θέλει απλώς συμπλήρωση, για να μην την ξαναγράψω από την αρχή. Αν θες, ανάρτησε (σε word) όσες θέλουν απλώς συμπλήρωση για να τις επιμεληθούμε.
- Συνημμένα
-
- Λύση GI_A_GEO_4_3731.doc
- (51 KiB) Μεταφορτώθηκε 140 φορές
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Ηλία καλησπέρα, εύλογη η ένστασή σου.hlkampel έγραψε:04. Άσκηση 4-3703
γ) Σημείωση: Αυτό το ερώτημα νομίζω έχει πρόβλημα.
i. Αν είναιτα σημεία
ταυτίζονται οπότε δεν υφίσταται τετράπλευρο
.
ii. Αντο
είναι ορθογώνιο.
Ας δεχτούμε ότι αφού αναφέρει ως διακριτά τα σημεία
 και
και  ότι το τρίγωνο δεν είναι ισοσκελές. Άντε να δεχτούμε το ίδιο και για το ορθογώνιο.
ότι το τρίγωνο δεν είναι ισοσκελές. Άντε να δεχτούμε το ίδιο και για το ορθογώνιο.Όμως.... αν
 , τότε το τραπέζιο είναι το
, τότε το τραπέζιο είναι το  κι όχι το
κι όχι το  !
!ΠΡΕΠΕΙ να συμπληρωθεί η εκφώνηση με τους περιορισμούς
 και
και  .
. Αναρωτιέμαι (και ζητώ τη γνώμη σας) Το ότι έχει συνοδευτικό ένα συγκεκριμένο σχήμα, δίχως να δηλώνεται στην υπόθεση, απαλλάσει τον λύτη από την υποχρέωση διερεύνησης;
Γενικότερα, είναι σωστό στη Γεωμετρία, να δίνονται ελλιπή στοιχεία στην υπόθεση και να περιγράφονται απλά με ένα σχήμα;
Ηλία, προτείνω να αναρτήσεις την παρατήρησή σου ΕΔΩ
τελευταία επεξεργασία από Γιώργος Ρίζος σε Τετ Οκτ 29, 2014 11:00 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
GK_A_GEO_4_3803
Σε τετράγωνο προεκτείνουμε τη διαγώνιο
προεκτείνουμε τη διαγώνιο 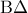 ( προς το
( προς το  ) κατά τμήμα
) κατά τμήμα  .
.
Έστω το μέσο της
το μέσο της  και
και  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  .
.
α) Να αποδείξετε ότι (Μονάδες 6)
(Μονάδες 6)
β) Να υπολογίσετε τις γωνίες του τριγώνου (Μονάδες 5)
(Μονάδες 5)
γ) να αποδείξετε ότι :
i. (Μονάδες 7)
(Μονάδες 7)
ii. (Μονάδες 7)
(Μονάδες 7)
Λύση
α) Επειδή και το
και το  είναι μέσο του
είναι μέσο του  ,στο τρίγωνο
,στο τρίγωνο 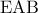 το
το  θα είναι μέσο της πλευράς
θα είναι μέσο της πλευράς  .
.
Τώρα το ευθύγραμμο τμήμα .
.
β) Το τρίγωνο είναι ορθογώνιο και ισοσκελές άρα οι οξείες του γωνίες θα είναι από
είναι ορθογώνιο και ισοσκελές άρα οι οξείες του γωνίες θα είναι από 
γ)
i. Οι διαγώνιοι του τετραγώνου , δηλαδή οι
, δηλαδή οι  και
και 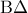 τέμνονται κάθετα .
τέμνονται κάθετα .
Στο τρίγωνο το ευθύγραμμο τμήμα
το ευθύγραμμο τμήμα  συνδέει τα μέσα των πλευρών του
συνδέει τα μέσα των πλευρών του 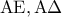 και άρα
και άρα  .
.
Δηλαδή και αφού
και αφού  θα είναι και
θα είναι και 
ii. Έστω το σημείο που η
το σημείο που η  τέμνει κάθετα (προηγούμενο ερώτημα) την
τέμνει κάθετα (προηγούμενο ερώτημα) την  .
.
Αφού και στο τρίγωνο
στο τρίγωνο  το σημείο
το σημείο  είναι ορθόκεντρο,
είναι ορθόκεντρο,
Συνεπώς η ευθεία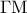 είναι ο φορέας του τρίτου του ύψους και ως εκ τούτου
είναι ο φορέας του τρίτου του ύψους και ως εκ τούτου  , έστω στο σημείο
, έστω στο σημείο  .
.
Φιλικά Νίκος
Σε τετράγωνο
 προεκτείνουμε τη διαγώνιο
προεκτείνουμε τη διαγώνιο 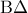 ( προς το
( προς το  ) κατά τμήμα
) κατά τμήμα  .
.Έστω
 το μέσο της
το μέσο της  και
και  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  .
.α) Να αποδείξετε ότι
 (Μονάδες 6)
(Μονάδες 6)β) Να υπολογίσετε τις γωνίες του τριγώνου
 (Μονάδες 5)
(Μονάδες 5)γ) να αποδείξετε ότι :
i.
 (Μονάδες 7)
(Μονάδες 7) ii.
 (Μονάδες 7)
(Μονάδες 7)Λύση
α) Επειδή
 και το
και το  είναι μέσο του
είναι μέσο του  ,στο τρίγωνο
,στο τρίγωνο 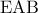 το
το  θα είναι μέσο της πλευράς
θα είναι μέσο της πλευράς  .
.Τώρα το ευθύγραμμο τμήμα
 .
.β) Το τρίγωνο
 είναι ορθογώνιο και ισοσκελές άρα οι οξείες του γωνίες θα είναι από
είναι ορθογώνιο και ισοσκελές άρα οι οξείες του γωνίες θα είναι από 
γ)
i. Οι διαγώνιοι του τετραγώνου
 , δηλαδή οι
, δηλαδή οι  και
και 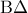 τέμνονται κάθετα .
τέμνονται κάθετα .Στο τρίγωνο
 το ευθύγραμμο τμήμα
το ευθύγραμμο τμήμα  συνδέει τα μέσα των πλευρών του
συνδέει τα μέσα των πλευρών του 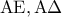 και άρα
και άρα  .
. Δηλαδή
 και αφού
και αφού  θα είναι και
θα είναι και 
ii. Έστω
 το σημείο που η
το σημείο που η  τέμνει κάθετα (προηγούμενο ερώτημα) την
τέμνει κάθετα (προηγούμενο ερώτημα) την  .
. Αφού και
 στο τρίγωνο
στο τρίγωνο  το σημείο
το σημείο  είναι ορθόκεντρο,
είναι ορθόκεντρο, Συνεπώς η ευθεία
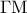 είναι ο φορέας του τρίτου του ύψους και ως εκ τούτου
είναι ο φορέας του τρίτου του ύψους και ως εκ τούτου  , έστω στο σημείο
, έστω στο σημείο  .
.Φιλικά Νίκος
- Συνημμένα
-
- Θέμα 4_4_3803.doc
- (112 KiB) Μεταφορτώθηκε 135 φορές
τελευταία επεξεργασία από Doloros σε Πέμ Οκτ 30, 2014 1:45 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
A_GEO_4_6876
Δίδεται ισοσκελές τρίγωνο . Φέρουμε τα ύψη του
. Φέρουμε τα ύψη του  και
και  .
.
Αν το μέσο της
το μέσο της  να αποδείξετε ότι :
να αποδείξετε ότι :
α) Το τρίγωνο είναι ισοσκελές ( Μονάδες 10)
είναι ισοσκελές ( Μονάδες 10)
β) Η είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  ( Μονάδες 15)
( Μονάδες 15)
Λύση
α) Οι είναι διάμεσοι προς την κοινή υποτείνουσα των ορθογωνίων τριγώνων
είναι διάμεσοι προς την κοινή υποτείνουσα των ορθογωνίων τριγώνων
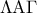 αφ ενός και
αφ ενός και  αφ ετέρου .
αφ ετέρου .
Θα είναι λοιπόν
β) Η απάντηση σ αυτό το ερώτημα χωρίς επί πλέον χάραξη γραμμών απαιτεί εγγράψιμα και ισότητα τριγώνων ( και όχι μόνο).
Θα δοθεί μια «γρήγορη» λύση που όμως δεν είναι εύκολο να την σκεφτεί ο μέσος μαθητής ειδικά σε ώρα εξετάσεων .
Από το φέρνουμε παράλληλη στην
φέρνουμε παράλληλη στην  που τέμνει τη
που τέμνει τη  στο
στο  .
.
Επειδή το είναι και μέσο της βάσης
είναι και μέσο της βάσης 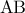 του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  θα είναι
θα είναι
 και άρα σε πρώτη «φάση» το τετράπλευρο
και άρα σε πρώτη «φάση» το τετράπλευρο  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.
Όμως λόγω του α) ερωτήματος θα είναι άρα το τετράπλευρο
άρα το τετράπλευρο  είναι ρόμβος.
είναι ρόμβος.
Ως εκ τούτου οι διαγώνιοι διχοτομούν τις γωνίες του του ρόμβου αυτού δηλαδή η είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
.
Υπάρχει πάντως και απλή λύση που δεν την "είδα", αλλά μου την υπέδειξαν . Δεν αλλάζω όμως τίποτα για παραδειγματισμό μου !
Φιλικά Νίκος
Δίδεται ισοσκελές τρίγωνο
 . Φέρουμε τα ύψη του
. Φέρουμε τα ύψη του  και
και  .
.Αν
 το μέσο της
το μέσο της  να αποδείξετε ότι :
να αποδείξετε ότι : α) Το τρίγωνο
 είναι ισοσκελές ( Μονάδες 10)
είναι ισοσκελές ( Μονάδες 10)β) Η
 είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  ( Μονάδες 15)
( Μονάδες 15)Λύση
α) Οι
 είναι διάμεσοι προς την κοινή υποτείνουσα των ορθογωνίων τριγώνων
είναι διάμεσοι προς την κοινή υποτείνουσα των ορθογωνίων τριγώνων 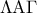 αφ ενός και
αφ ενός και  αφ ετέρου .
αφ ετέρου .Θα είναι λοιπόν

β) Η απάντηση σ αυτό το ερώτημα χωρίς επί πλέον χάραξη γραμμών απαιτεί εγγράψιμα και ισότητα τριγώνων ( και όχι μόνο).
Θα δοθεί μια «γρήγορη» λύση που όμως δεν είναι εύκολο να την σκεφτεί ο μέσος μαθητής ειδικά σε ώρα εξετάσεων .
Από το
 φέρνουμε παράλληλη στην
φέρνουμε παράλληλη στην  που τέμνει τη
που τέμνει τη  στο
στο  .
.Επειδή το
 είναι και μέσο της βάσης
είναι και μέσο της βάσης 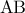 του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  θα είναι
θα είναι  και άρα σε πρώτη «φάση» το τετράπλευρο
και άρα σε πρώτη «φάση» το τετράπλευρο  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. Όμως λόγω του α) ερωτήματος θα είναι
 άρα το τετράπλευρο
άρα το τετράπλευρο  είναι ρόμβος.
είναι ρόμβος.Ως εκ τούτου οι διαγώνιοι διχοτομούν τις γωνίες του του ρόμβου αυτού δηλαδή η
 είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
.Υπάρχει πάντως και απλή λύση που δεν την "είδα", αλλά μου την υπέδειξαν . Δεν αλλάζω όμως τίποτα για παραδειγματισμό μου !
Φιλικά Νίκος
- Συνημμένα
-
- Θέμα 4_6876.doc
- (71.5 KiB) Μεταφορτώθηκε 145 φορές
τελευταία επεξεργασία από Doloros σε Πέμ Οκτ 30, 2014 9:04 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Άσκηση 4-3767
Δίνεται κύκλος και μία επίκεντρη γωνία του
και μία επίκεντρη γωνία του 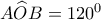 . Οι εφαπτόμενες του κύκλου στα σημεία
. Οι εφαπτόμενες του κύκλου στα σημεία  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Θεωρούμε σημείο
. Θεωρούμε σημείο  του τόξου
του τόξου  και φέρνουμε τις χορδές
και φέρνουμε τις χορδές  και
και  , οι οποίες προεκτεινόμενες τέμνουν τις
, οι οποίες προεκτεινόμενες τέμνουν τις  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα.
Να αποδείξετε ότι:
α) Το τρίγωνο είναι ισόπλευρο. (Μονάδες
είναι ισόπλευρο. (Μονάδες  )
)
β) . (Μονάδες
. (Μονάδες  )
)
γ) Τα τρίγωνα και
και  είναι ίσα. (Μονάδες
είναι ίσα. (Μονάδες  )
)
Λύση.
α) Το τετράπλευρο είναι εγγράψιμο(δύο απέναντι γωνίες του είναι ορθές), άρα
είναι εγγράψιμο(δύο απέναντι γωνίες του είναι ορθές), άρα  . Το τρίγωνο
. Το τρίγωνο 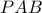 είναι ισοσκελές (
είναι ισοσκελές ( ) και έχει μία γωνία
) και έχει μία γωνία  , οπότε είναι ισόπλευρο.
, οπότε είναι ισόπλευρο.
β)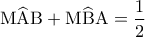 (τόξο
(τόξο τόξο
τόξο )
) (τόξο
(τόξο )
) .
.
γ) Τα τρίγωνα και
και  έχουν:
έχουν:
 ,
,  (λόγω του ισοπλεύρου τριγώνου
(λόγω του ισοπλεύρου τριγώνου 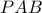 ) και
) και  (σχέση εγγεγραμμένης γωνίας με γωνία χορδής κι εφαπτομένης), άρα είναι ίσα
(σχέση εγγεγραμμένης γωνίας με γωνία χορδής κι εφαπτομένης), άρα είναι ίσα  .
.
Δίνεται κύκλος
 και μία επίκεντρη γωνία του
και μία επίκεντρη γωνία του 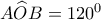 . Οι εφαπτόμενες του κύκλου στα σημεία
. Οι εφαπτόμενες του κύκλου στα σημεία  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Θεωρούμε σημείο
. Θεωρούμε σημείο  του τόξου
του τόξου  και φέρνουμε τις χορδές
και φέρνουμε τις χορδές  και
και  , οι οποίες προεκτεινόμενες τέμνουν τις
, οι οποίες προεκτεινόμενες τέμνουν τις  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα. Να αποδείξετε ότι:
α) Το τρίγωνο
 είναι ισόπλευρο. (Μονάδες
είναι ισόπλευρο. (Μονάδες  )
) β)
 . (Μονάδες
. (Μονάδες  )
)γ) Τα τρίγωνα
 και
και  είναι ίσα. (Μονάδες
είναι ίσα. (Μονάδες  )
)Λύση.
α) Το τετράπλευρο
 είναι εγγράψιμο(δύο απέναντι γωνίες του είναι ορθές), άρα
είναι εγγράψιμο(δύο απέναντι γωνίες του είναι ορθές), άρα  . Το τρίγωνο
. Το τρίγωνο 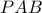 είναι ισοσκελές (
είναι ισοσκελές ( ) και έχει μία γωνία
) και έχει μία γωνία  , οπότε είναι ισόπλευρο.
, οπότε είναι ισόπλευρο.β)
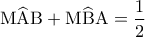 (τόξο
(τόξο τόξο
τόξο )
) (τόξο
(τόξο )
) .
.γ) Τα τρίγωνα
 και
και  έχουν:
έχουν: ,
,  (λόγω του ισοπλεύρου τριγώνου
(λόγω του ισοπλεύρου τριγώνου 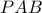 ) και
) και  (σχέση εγγεγραμμένης γωνίας με γωνία χορδής κι εφαπτομένης), άρα είναι ίσα
(σχέση εγγεγραμμένης γωνίας με γωνία χορδής κι εφαπτομένης), άρα είναι ίσα  .
.- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Άσκηση 4-3813
Δίνεται παραλληλόγραμμο με
με  και τη γωνία
και τη γωνία  αμβλεία. Από την κορυφή
αμβλεία. Από την κορυφή  φέρουμε την
φέρουμε την  κάθετη στην ευθεία
κάθετη στην ευθεία  και έστω
και έστω  τα μέσα των
τα μέσα των 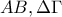 αντίστοιχα.
αντίστοιχα.
Να αποδείξετε ότι:
α) Το τετράπλευρο είναι ρόμβος. (Μονάδες
είναι ρόμβος. (Μονάδες  )
)
β) Το τετράπλευρο είναι ισοσκελές τραπέζιο. (Μονάδες
είναι ισοσκελές τραπέζιο. (Μονάδες  )
)
γ) Η είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  . (Μονάδες
. (Μονάδες  )
)
Λύση.
α) , οπότε το
, οπότε το  είναι παραλληλόγραμμο. Αλλά
είναι παραλληλόγραμμο. Αλλά  , άρα τελικά είναι ρόμβος.
, άρα τελικά είναι ρόμβος.
β) Η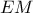 είναι η διάμεσος που αντιστοιχεί στην υποτείνουσα του ορθογωνίου τριγώνου
είναι η διάμεσος που αντιστοιχεί στην υποτείνουσα του ορθογωνίου τριγώνου  , οπότε
, οπότε  . Είναι ακόμα
. Είναι ακόμα  και επιπλέον
και επιπλέον 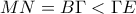 (Επειδή η γωνία
(Επειδή η γωνία  είναι αμβλεία το
είναι αμβλεία το  βρίσκεται στην προέκταση της
βρίσκεται στην προέκταση της  ). Άρα το τετράπλευρο
). Άρα το τετράπλευρο  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.
γ) Το ως ισοσκελές τραπέζιο είναι εγγράψιμο, οπότε
ως ισοσκελές τραπέζιο είναι εγγράψιμο, οπότε  (εγγεγραμμένες γωνίες που βαίνουν σε αντίστοιχα τόξα ίσων χορδών).
(εγγεγραμμένες γωνίες που βαίνουν σε αντίστοιχα τόξα ίσων χορδών).
ΣΗΜΕΙΩΣΗ: Επειδή η εκφώνηση της άσκησης δεν συνοδεύεται από σχήμα, νομίζω ότι θα έπρεπε να διευκρινιστεί ότι το είναι σημείο της ευθείας
είναι σημείο της ευθείας 
Δίνεται παραλληλόγραμμο
 με
με  και τη γωνία
και τη γωνία  αμβλεία. Από την κορυφή
αμβλεία. Από την κορυφή  φέρουμε την
φέρουμε την  κάθετη στην ευθεία
κάθετη στην ευθεία  και έστω
και έστω  τα μέσα των
τα μέσα των 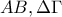 αντίστοιχα.
αντίστοιχα.Να αποδείξετε ότι:
α) Το τετράπλευρο
 είναι ρόμβος. (Μονάδες
είναι ρόμβος. (Μονάδες  )
)β) Το τετράπλευρο
 είναι ισοσκελές τραπέζιο. (Μονάδες
είναι ισοσκελές τραπέζιο. (Μονάδες  )
)γ) Η
 είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  . (Μονάδες
. (Μονάδες  )
)Λύση.
α)
 , οπότε το
, οπότε το  είναι παραλληλόγραμμο. Αλλά
είναι παραλληλόγραμμο. Αλλά  , άρα τελικά είναι ρόμβος.
, άρα τελικά είναι ρόμβος.β) Η
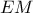 είναι η διάμεσος που αντιστοιχεί στην υποτείνουσα του ορθογωνίου τριγώνου
είναι η διάμεσος που αντιστοιχεί στην υποτείνουσα του ορθογωνίου τριγώνου  , οπότε
, οπότε  . Είναι ακόμα
. Είναι ακόμα  και επιπλέον
και επιπλέον 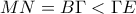 (Επειδή η γωνία
(Επειδή η γωνία  είναι αμβλεία το
είναι αμβλεία το  βρίσκεται στην προέκταση της
βρίσκεται στην προέκταση της  ). Άρα το τετράπλευρο
). Άρα το τετράπλευρο  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.γ) Το
 ως ισοσκελές τραπέζιο είναι εγγράψιμο, οπότε
ως ισοσκελές τραπέζιο είναι εγγράψιμο, οπότε  (εγγεγραμμένες γωνίες που βαίνουν σε αντίστοιχα τόξα ίσων χορδών).
(εγγεγραμμένες γωνίες που βαίνουν σε αντίστοιχα τόξα ίσων χορδών).ΣΗΜΕΙΩΣΗ: Επειδή η εκφώνηση της άσκησης δεν συνοδεύεται από σχήμα, νομίζω ότι θα έπρεπε να διευκρινιστεί ότι το
 είναι σημείο της ευθείας
είναι σημείο της ευθείας 
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
GI_A_GEO_4_4555
Δίνεται τρίγωνο . Από το μέσο
. Από το μέσο  του
του  φέρουμε ευθύγραμμο τμήμα
φέρουμε ευθύγραμμο τμήμα  ίσο και παράλληλο με το
ίσο και παράλληλο με το  και ευθύγραμμο τμήμα
και ευθύγραμμο τμήμα  ίσο και παράλληλο με το
ίσο και παράλληλο με το  (τα σημεία
(τα σημεία  και
και  είναι στο ημιεπίπεδο που ορίζεται από τo
είναι στο ημιεπίπεδο που ορίζεται από τo  και το σημείο
και το σημείο  ). Να αποδείξετε ότι:
). Να αποδείξετε ότι:
α) Τα σημεία είναι συνευθειακά. (Μονάδες 10)
είναι συνευθειακά. (Μονάδες 10)
β) Η περίμετρος του τριγώνου είναι ίση με την περίμετρο του τριγώνου
είναι ίση με την περίμετρο του τριγώνου  . (Μονάδες 9)
. (Μονάδες 9)
γ) Όταν ένας καθηγητής έθεσε στους μαθητές του το ερώτημα αν τα σημεία είναι συνευθειακά, ένας από αυτούς έκανε το παρακάτω σχήμα και απάντησε ως εξής:
είναι συνευθειακά, ένας από αυτούς έκανε το παρακάτω σχήμα και απάντησε ως εξής:
 (εντός εναλλάξ των ΑΒ//ΜΔ που τέμνονται από ΑΖ)
(εντός εναλλάξ των ΑΒ//ΜΔ που τέμνονται από ΑΖ)
 (εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ)
(εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ)
Όμως (άθροισμα γωνιών του τριγώνου ΑΔΖ). Άρα σύμφωνα με τα προηγούμενα έχουμε:
(άθροισμα γωνιών του τριγώνου ΑΔΖ). Άρα σύμφωνα με τα προηγούμενα έχουμε:  . Οπότε
. Οπότε  συνευθειακά.
συνευθειακά.
Όμως ο καθηγητής είπε ότι υπάρχει λάθος στο συλλογισμό. Μπορείτε να εντοπίσετε το λάθος του μαθητή; (Μονάδες 6) α) Αφού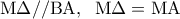 το
το  είναι παραλληλόγραμμο. Ομοίως, αφού
είναι παραλληλόγραμμο. Ομοίως, αφού  και το
και το  είναι παραλληλόγραμμο, οπότε
είναι παραλληλόγραμμο, οπότε  και αφού οι
και αφού οι  έχουν κοινό σημείο το
έχουν κοινό σημείο το  είναι συνευθειακά τμήματα, άρα τα σημεία
είναι συνευθειακά τμήματα, άρα τα σημεία είναι συνευθειακά.
είναι συνευθειακά.
β) Ακόμα, είναι , οπότε
, οπότε  .
.
Άρα είναι Περίμετρος = Περίμετρος
= Περίμετρος 
γ) Το λάθος του μαθητή είναι στην πρόταση: (εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ), αφού δεν έχουμε αποδείξει ότι το
(εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ), αφού δεν έχουμε αποδείξει ότι το  είναι προέκταση της
είναι προέκταση της  .
.
(Αυτό είναι το ζητούμενο της απόδειξης…)
ΣΧΟΛΙΟ: Το δεδομένο ότι το είναι μέσο της
είναι μέσο της  είναι περιττό.
είναι περιττό.
Δίνεται τρίγωνο
 . Από το μέσο
. Από το μέσο  του
του  φέρουμε ευθύγραμμο τμήμα
φέρουμε ευθύγραμμο τμήμα  ίσο και παράλληλο με το
ίσο και παράλληλο με το  και ευθύγραμμο τμήμα
και ευθύγραμμο τμήμα  ίσο και παράλληλο με το
ίσο και παράλληλο με το  (τα σημεία
(τα σημεία  και
και  είναι στο ημιεπίπεδο που ορίζεται από τo
είναι στο ημιεπίπεδο που ορίζεται από τo  και το σημείο
και το σημείο  ). Να αποδείξετε ότι:
). Να αποδείξετε ότι: α) Τα σημεία
 είναι συνευθειακά. (Μονάδες 10)
είναι συνευθειακά. (Μονάδες 10) β) Η περίμετρος του τριγώνου
 είναι ίση με την περίμετρο του τριγώνου
είναι ίση με την περίμετρο του τριγώνου  . (Μονάδες 9)
. (Μονάδες 9) γ) Όταν ένας καθηγητής έθεσε στους μαθητές του το ερώτημα αν τα σημεία
 είναι συνευθειακά, ένας από αυτούς έκανε το παρακάτω σχήμα και απάντησε ως εξής:
είναι συνευθειακά, ένας από αυτούς έκανε το παρακάτω σχήμα και απάντησε ως εξής: (εντός εναλλάξ των ΑΒ//ΜΔ που τέμνονται από ΑΖ)
(εντός εναλλάξ των ΑΒ//ΜΔ που τέμνονται από ΑΖ)  (εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ)
(εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ) Όμως
 (άθροισμα γωνιών του τριγώνου ΑΔΖ). Άρα σύμφωνα με τα προηγούμενα έχουμε:
(άθροισμα γωνιών του τριγώνου ΑΔΖ). Άρα σύμφωνα με τα προηγούμενα έχουμε:  . Οπότε
. Οπότε  συνευθειακά.
συνευθειακά.Όμως ο καθηγητής είπε ότι υπάρχει λάθος στο συλλογισμό. Μπορείτε να εντοπίσετε το λάθος του μαθητή; (Μονάδες 6) α) Αφού
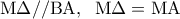 το
το  είναι παραλληλόγραμμο. Ομοίως, αφού
είναι παραλληλόγραμμο. Ομοίως, αφού  και το
και το  είναι παραλληλόγραμμο, οπότε
είναι παραλληλόγραμμο, οπότε  και αφού οι
και αφού οι  έχουν κοινό σημείο το
έχουν κοινό σημείο το  είναι συνευθειακά τμήματα, άρα τα σημεία
είναι συνευθειακά τμήματα, άρα τα σημεία είναι συνευθειακά.
είναι συνευθειακά.β) Ακόμα, είναι
 , οπότε
, οπότε  .
.Άρα είναι Περίμετρος
 = Περίμετρος
= Περίμετρος 
γ) Το λάθος του μαθητή είναι στην πρόταση:
 (εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ), αφού δεν έχουμε αποδείξει ότι το
(εντός εκτός και επί τα αυτά μέρη των ΑΒ//ΜΔ που τέμνονται από ΔΕ), αφού δεν έχουμε αποδείξει ότι το  είναι προέκταση της
είναι προέκταση της  .
. (Αυτό είναι το ζητούμενο της απόδειξης…)
ΣΧΟΛΙΟ: Το δεδομένο ότι το
 είναι μέσο της
είναι μέσο της  είναι περιττό.
είναι περιττό.- Συνημμένα
-
- Λύση GI_A_GEO_4_4555.doc
- (101 KiB) Μεταφορτώθηκε 124 φορές
-
- GI_A_GEO_4_4555.ggb
- (6.86 KiB) Μεταφορτώθηκε 121 φορές
τελευταία επεξεργασία από Γιώργος Ρίζος σε Πέμ Οκτ 30, 2014 10:39 pm, έχει επεξεργασθεί 3 φορές συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Άσκηση 4-4614
Δίνεται τετράγωνο και τυχαίο σημείο
και τυχαίο σημείο  στην πλευρά
στην πλευρά 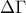 . Φέρουμε τη διχοτόμο
. Φέρουμε τη διχοτόμο  της γωνίας
της γωνίας  και τη
και τη  κάθετη από το
κάθετη από το  προς την
προς την  , η οποία τέμνει την
, η οποία τέμνει την  στο
στο  και την
και την  στο
στο  .
.
Να αποδείξετε ότι:
α) Τα τρίγωνα και
και  είναι ίσα. (Μονάδες
είναι ίσα. (Μονάδες  )
)
β) και
και  . (Μονάδες
. (Μονάδες  )
)
γ) . (Μονάδες
. (Μονάδες  )
)
Λύση:
α) Τα τρίγωνα και
και  είναι ορθογώνια και έχουν
είναι ορθογώνια και έχουν 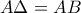 (ως πλευρές τετραγώνου) και
(ως πλευρές τετραγώνου) και  (είναι οξείες γωνίες με πλευρές κάθετες). Άρα τα τρίγωνα είναι ίσα.
(είναι οξείες γωνίες με πλευρές κάθετες). Άρα τα τρίγωνα είναι ίσα.
β) Στο τρίγωνο το
το  είναι ύψος και διχοτόμος, οπότε είναι ισοσκελές. Δηλαδή
είναι ύψος και διχοτόμος, οπότε είναι ισοσκελές. Δηλαδή  και
και  .
.  (ως κατακορυφήν).
(ως κατακορυφήν).  (ως εντός εναλλάξ).
(ως εντός εναλλάξ).
Άρα:
γ)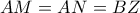 ,
,  . Οπότε:
. Οπότε: 
Δίνεται τετράγωνο
 και τυχαίο σημείο
και τυχαίο σημείο  στην πλευρά
στην πλευρά 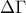 . Φέρουμε τη διχοτόμο
. Φέρουμε τη διχοτόμο  της γωνίας
της γωνίας  και τη
και τη  κάθετη από το
κάθετη από το  προς την
προς την  , η οποία τέμνει την
, η οποία τέμνει την  στο
στο  και την
και την  στο
στο  .
.Να αποδείξετε ότι:
α) Τα τρίγωνα
 και
και  είναι ίσα. (Μονάδες
είναι ίσα. (Μονάδες  )
)β)
 και
και  . (Μονάδες
. (Μονάδες  )
)γ)
 . (Μονάδες
. (Μονάδες  )
)Λύση:
α) Τα τρίγωνα
 και
και  είναι ορθογώνια και έχουν
είναι ορθογώνια και έχουν 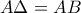 (ως πλευρές τετραγώνου) και
(ως πλευρές τετραγώνου) και  (είναι οξείες γωνίες με πλευρές κάθετες). Άρα τα τρίγωνα είναι ίσα.
(είναι οξείες γωνίες με πλευρές κάθετες). Άρα τα τρίγωνα είναι ίσα.β) Στο τρίγωνο
 το
το  είναι ύψος και διχοτόμος, οπότε είναι ισοσκελές. Δηλαδή
είναι ύψος και διχοτόμος, οπότε είναι ισοσκελές. Δηλαδή  και
και  .
.  (ως κατακορυφήν).
(ως κατακορυφήν).  (ως εντός εναλλάξ).
(ως εντός εναλλάξ).Άρα:

γ)
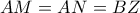 ,
,  . Οπότε:
. Οπότε: 
τελευταία επεξεργασία από george visvikis σε Πέμ Οκτ 30, 2014 11:07 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Άσκηση 4-4778
Σε παραλληλόγραμμο με
με  και
και  θεωρούμε σημείο
θεωρούμε σημείο  στην προέκταση της
στην προέκταση της  (προς το
(προς το  ) τέτοιο ώστε
) τέτοιο ώστε  .
.
Αν είναι σημείο της
είναι σημείο της 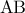 , τέτοιο ώστε
, τέτοιο ώστε 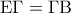 , να αποδείξετε ότι:
, να αποδείξετε ότι:
α) Η γωνία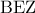 είναι ορθή. (Μονάδες 8)
είναι ορθή. (Μονάδες 8)
β) Το τετράπλευρο είναι ισοσκελές τραπέζιο. (Μονάδες 8)
είναι ισοσκελές τραπέζιο. (Μονάδες 8)
γ) Το τετράπλευρο είναι παραλληλόγραμμο. (Μονάδες 9)
είναι παραλληλόγραμμο. (Μονάδες 9)
Λύση
α) Στο τρίγωνο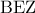 η διάμεσός του
η διάμεσός του 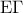 είναι το μισό της αντίστοιχης πλευράς της.
είναι το μισό της αντίστοιχης πλευράς της.
Άρα το τρίγωνο είναι ορθογώνιο με
β) Είναι και
και 
Η ευθεία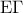 τέμνει την
τέμνει την  άρα θα τέμνει και την παράλληλή της
άρα θα τέμνει και την παράλληλή της  .
.
Έτσι το τετράπλευρο είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.
γ) Είναι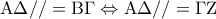 οπότε το
οπότε το  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.
Σε παραλληλόγραμμο
 με
με  και
και  θεωρούμε σημείο
θεωρούμε σημείο  στην προέκταση της
στην προέκταση της  (προς το
(προς το  ) τέτοιο ώστε
) τέτοιο ώστε  .
. Αν
 είναι σημείο της
είναι σημείο της 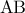 , τέτοιο ώστε
, τέτοιο ώστε 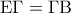 , να αποδείξετε ότι:
, να αποδείξετε ότι:α) Η γωνία
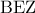 είναι ορθή. (Μονάδες 8)
είναι ορθή. (Μονάδες 8)β) Το τετράπλευρο
 είναι ισοσκελές τραπέζιο. (Μονάδες 8)
είναι ισοσκελές τραπέζιο. (Μονάδες 8)γ) Το τετράπλευρο
 είναι παραλληλόγραμμο. (Μονάδες 9)
είναι παραλληλόγραμμο. (Μονάδες 9)Λύση
α) Στο τρίγωνο
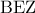 η διάμεσός του
η διάμεσός του 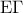 είναι το μισό της αντίστοιχης πλευράς της.
είναι το μισό της αντίστοιχης πλευράς της. Άρα το τρίγωνο είναι ορθογώνιο με

β) Είναι
 και
και 
Η ευθεία
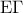 τέμνει την
τέμνει την  άρα θα τέμνει και την παράλληλή της
άρα θα τέμνει και την παράλληλή της  .
.Έτσι το τετράπλευρο
 είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.γ) Είναι
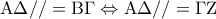 οπότε το
οπότε το  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.- Συνημμένα
-
- 4778.doc
- (86 KiB) Μεταφορτώθηκε 144 φορές
Ηλίας Καμπελής
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Ένας άλλος τρόπος για το β) ερώτημα της άσκησης 4-6876.
Δίδεται ισοσκελές τρίγωνο . Φέρουμε τα ύψη του
. Φέρουμε τα ύψη του  και
και  .
.
Αν το μέσο της
το μέσο της  να αποδείξετε ότι :
να αποδείξετε ότι :
α) Το τρίγωνο είναι ισοσκελές ( Μονάδες 10)
είναι ισοσκελές ( Μονάδες 10)
β) Η είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  ( Μονάδες 15)
( Μονάδες 15)
Λύση.
β) Από το ισοσκελές τρίγωνο , έχουμε
, έχουμε 
Η ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών 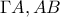 του τριγώνου
του τριγώνου  , οπότε,
, οπότε,  . Άρα:
. Άρα: 
Δίδεται ισοσκελές τρίγωνο
 . Φέρουμε τα ύψη του
. Φέρουμε τα ύψη του  και
και  .
.Αν
 το μέσο της
το μέσο της  να αποδείξετε ότι :
να αποδείξετε ότι : α) Το τρίγωνο
 είναι ισοσκελές ( Μονάδες 10)
είναι ισοσκελές ( Μονάδες 10)β) Η
 είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  ( Μονάδες 15)
( Μονάδες 15)Λύση.
β) Από το ισοσκελές τρίγωνο
 , έχουμε
, έχουμε 
Η
 ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών 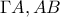 του τριγώνου
του τριγώνου  , οπότε,
, οπότε,  . Άρα:
. Άρα: 
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
GI_A_GEO_4_4794
Δίνεται ορθογώνιο τρίγωνο
 με
με  διχοτόμο και
διχοτόμο και  ύψος, που τέμνονται στο
ύψος, που τέμνονται στο  . Η κάθετη από το
. Η κάθετη από το  στην
στην  τέμνει τις
τέμνει τις  και
και  στα
στα  και
και  αντίστοιχα.
αντίστοιχα.
α) Να αποδείξετε ότι:
i. Tα τρίγωνα και
και  είναι ίσα. (Μονάδες 6)
είναι ίσα. (Μονάδες 6)
ii. Tο τρίγωνο είναι ισοσκελές. (Μονάδες 6)
είναι ισοσκελές. (Μονάδες 6)
iii. Η είναι κάθετη στην
είναι κάθετη στην  . (Μονάδες 7)
. (Μονάδες 7)
β) Αν επιπλέον το ορθογώνιο τρίγωνο είναι και ισοσκελές, να αποδείξετε ότι η
είναι και ισοσκελές, να αποδείξετε ότι η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  . (Μονάδες 6)
. (Μονάδες 6)
αi) Το ανήκει στη διχοτόμο της
ανήκει στη διχοτόμο της  , άρα ισαπέχει από τις
, άρα ισαπέχει από τις  , δηλαδή είναι
, δηλαδή είναι 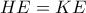 .
.
Τα ορθογώνια τρίγωνα και
και  έχουν
έχουν 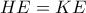 , όπως αποδείξαμε και
, όπως αποδείξαμε και  ως κατακορυφήν γωνίες, άρα είναι ίσα.
ως κατακορυφήν γωνίες, άρα είναι ίσα.
ii) Τα ορθογώνια τρίγωνα και
και  έχουν τη
έχουν τη  κοινή,
κοινή, 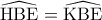 από υπόθεση, άρα είναι ίσα, οπότε είναι
από υπόθεση, άρα είναι ίσα, οπότε είναι  , δηλαδή
, δηλαδή  ισοσκελές.
ισοσκελές.
iii) Στο το
το  είναι ορθόκεντρο, αφού είναι σημείο τομής των υψών
είναι ορθόκεντρο, αφού είναι σημείο τομής των υψών 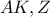 , οπότε και το
, οπότε και το  ανήκει στο ύψος από το
ανήκει στο ύψος από το  στην
στην  .
.
β) Αν ορθογώνιο με
ορθογώνιο με  και ισοσκελές, τότε το ύψος
και ισοσκελές, τότε το ύψος  είναι και διχοτόμος, οπότε το
είναι και διχοτόμος, οπότε το  είναι έγκεντρο του
είναι έγκεντρο του  , άρα και η
, άρα και η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
.
Δίνεται ορθογώνιο τρίγωνο

 με
με  διχοτόμο και
διχοτόμο και  ύψος, που τέμνονται στο
ύψος, που τέμνονται στο  . Η κάθετη από το
. Η κάθετη από το  στην
στην  τέμνει τις
τέμνει τις  και
και  στα
στα  και
και  αντίστοιχα.
αντίστοιχα. α) Να αποδείξετε ότι:
i. Tα τρίγωνα
 και
και  είναι ίσα. (Μονάδες 6)
είναι ίσα. (Μονάδες 6) ii. Tο τρίγωνο
 είναι ισοσκελές. (Μονάδες 6)
είναι ισοσκελές. (Μονάδες 6) iii. Η
 είναι κάθετη στην
είναι κάθετη στην  . (Μονάδες 7)
. (Μονάδες 7) β) Αν επιπλέον το ορθογώνιο τρίγωνο
 είναι και ισοσκελές, να αποδείξετε ότι η
είναι και ισοσκελές, να αποδείξετε ότι η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  . (Μονάδες 6)
. (Μονάδες 6) αi) Το
 ανήκει στη διχοτόμο της
ανήκει στη διχοτόμο της  , άρα ισαπέχει από τις
, άρα ισαπέχει από τις  , δηλαδή είναι
, δηλαδή είναι 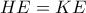 .
.Τα ορθογώνια τρίγωνα
 και
και  έχουν
έχουν 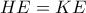 , όπως αποδείξαμε και
, όπως αποδείξαμε και  ως κατακορυφήν γωνίες, άρα είναι ίσα.
ως κατακορυφήν γωνίες, άρα είναι ίσα.ii) Τα ορθογώνια τρίγωνα
 και
και  έχουν τη
έχουν τη  κοινή,
κοινή, 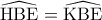 από υπόθεση, άρα είναι ίσα, οπότε είναι
από υπόθεση, άρα είναι ίσα, οπότε είναι  , δηλαδή
, δηλαδή  ισοσκελές.
ισοσκελές.iii) Στο
 το
το  είναι ορθόκεντρο, αφού είναι σημείο τομής των υψών
είναι ορθόκεντρο, αφού είναι σημείο τομής των υψών 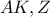 , οπότε και το
, οπότε και το  ανήκει στο ύψος από το
ανήκει στο ύψος από το  στην
στην  .
.β) Αν
 ορθογώνιο με
ορθογώνιο με  και ισοσκελές, τότε το ύψος
και ισοσκελές, τότε το ύψος  είναι και διχοτόμος, οπότε το
είναι και διχοτόμος, οπότε το  είναι έγκεντρο του
είναι έγκεντρο του  , άρα και η
, άρα και η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
.- Συνημμένα
-
- Λύση GI_A_GEO_4_4794.doc
- (120 KiB) Μεταφορτώθηκε 110 φορές
-
- GI_A_GEO_4_4794.ggb
- (7.04 KiB) Μεταφορτώθηκε 89 φορές
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Άσκηση GI_A_GEO_4_4808
Δίνονται δυο ίσα ισοσκελή τρίγωνα και
και , τέτοια ώστε οι πλευρές τους
, τέτοια ώστε οι πλευρές τους  και
και  να τέμνονται κάθετα στο σημείο
να τέμνονται κάθετα στο σημείο  , όπως φαίνεται στο παρακάτω σχήμα. Τα σημεία
, όπως φαίνεται στο παρακάτω σχήμα. Τα σημεία  και
και  είναι τα μέσα των τμημάτων
είναι τα μέσα των τμημάτων  και
και αντίστοιχα.
αντίστοιχα.
Να αποδείξετε ότι:
α)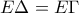 . (Μονάδες
. (Μονάδες  )
)
β) . (Μονάδες
. (Μονάδες  )
)
γ) Το τρίγωνο είναι ισοσκελές και
είναι ισοσκελές και  . (Μονάδες
. (Μονάδες  )
)
Λύση.
α) Από τα ίσα ισοσκελή τρίγωνα έχουμε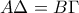 και
και  , οπότε τα ορθογώνια τρίγωνα
, οπότε τα ορθογώνια τρίγωνα 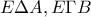 είναι ίσα. Άρα
είναι ίσα. Άρα 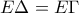
β) Είναι ακόμα , δηλαδή τα τρίγωνα
, δηλαδή τα τρίγωνα  είναι ορθογώνια και ισοσκελή, οπότε:
είναι ορθογώνια και ισοσκελή, οπότε: 
γ) Επειδή η διάμεσος ορθογωνίου τριγώνου που αντιστοιχεί στην υποτείνουσα είναι ίση με το μισό της, θα έχουμε: , οπότε το τρίγωνο
, οπότε το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.
Η είναι διάμεσος του ισοσκελούς τραπεζίου
είναι διάμεσος του ισοσκελούς τραπεζίου  , άρα
, άρα  .
.
ΣΧΟΛΙΟ: Η κατασκευή του σχήματος είναι δύσκολη για μαθητές, επειδή δεν έχουμε απλώς δύο ίσα ισοσκελή τρίγωνα, αλλά ισοσκελή τρίγωνα με συγκεκριμένες γωνίες ( ).
).
Δίνονται δυο ίσα ισοσκελή τρίγωνα
 και
και , τέτοια ώστε οι πλευρές τους
, τέτοια ώστε οι πλευρές τους  και
και  να τέμνονται κάθετα στο σημείο
να τέμνονται κάθετα στο σημείο  , όπως φαίνεται στο παρακάτω σχήμα. Τα σημεία
, όπως φαίνεται στο παρακάτω σχήμα. Τα σημεία  και
και  είναι τα μέσα των τμημάτων
είναι τα μέσα των τμημάτων  και
και αντίστοιχα.
αντίστοιχα.Να αποδείξετε ότι:
α)
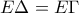 . (Μονάδες
. (Μονάδες  )
)β)
 . (Μονάδες
. (Μονάδες  )
)γ) Το τρίγωνο
 είναι ισοσκελές και
είναι ισοσκελές και  . (Μονάδες
. (Μονάδες  )
)Λύση.
α) Από τα ίσα ισοσκελή τρίγωνα έχουμε
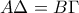 και
και  , οπότε τα ορθογώνια τρίγωνα
, οπότε τα ορθογώνια τρίγωνα 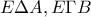 είναι ίσα. Άρα
είναι ίσα. Άρα 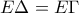
β) Είναι ακόμα
 , δηλαδή τα τρίγωνα
, δηλαδή τα τρίγωνα  είναι ορθογώνια και ισοσκελή, οπότε:
είναι ορθογώνια και ισοσκελή, οπότε: 
γ) Επειδή η διάμεσος ορθογωνίου τριγώνου που αντιστοιχεί στην υποτείνουσα είναι ίση με το μισό της, θα έχουμε:
 , οπότε το τρίγωνο
, οπότε το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.Η
 είναι διάμεσος του ισοσκελούς τραπεζίου
είναι διάμεσος του ισοσκελούς τραπεζίου  , άρα
, άρα  .
.ΣΧΟΛΙΟ: Η κατασκευή του σχήματος είναι δύσκολη για μαθητές, επειδή δεν έχουμε απλώς δύο ίσα ισοσκελή τρίγωνα, αλλά ισοσκελή τρίγωνα με συγκεκριμένες γωνίες (
 ).
).Re: ΝΕΑ ΘΕΜΑΤΑ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ 4ο ΘΕΜΑ
Μια διαφορετική λύση για το β) ΤοDoloros έγραψε: Δίδεται ισοσκελές τρίγωνο. Φέρουμε τα ύψη του
και
.
Αντο μέσο της
να αποδείξετε ότι :
α) Το τρίγωνοείναι ισοσκελές ( Μονάδες 10)
β) Ηείναι διχοτόμος της γωνίας
( Μονάδες 15)
Λύση
Στο β) υπάρχει και απλή λύση που δεν την "είδα" . Φιλικά Νίκος
 είναι ισοσκλές τραπέζιο ( δεν ξέρω αν ο Νίκος εννοεί αυτή )
είναι ισοσκλές τραπέζιο ( δεν ξέρω αν ο Νίκος εννοεί αυτή )Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
