Δίνεται παραλληλόγραμμο με
 το κέντρο του. Από την κορυφή
το κέντρο του. Από την κορυφή  φέρουμε το τμήμα
φέρουμε το τμήμα  κάθετο στην
κάθετο στην  και στην προέκτασή του προς το
και στην προέκτασή του προς το  θεωρούμε σημείο
θεωρούμε σημείο  , ώστε
, ώστε  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:α)
 (Μονάδες
(Μονάδες  )
)β) Η γωνία
 είναι ορθή. (Μονάδες
είναι ορθή. (Μονάδες  )
)γ) Το τετράπλευρο
 είναι ισοσκελές τραπέζιο. (Μονάδες
είναι ισοσκελές τραπέζιο. (Μονάδες  )
)Λύση:
α) Το τρίγωνο
 είναι ισοσκελές, επειδή η
είναι ισοσκελές, επειδή η  είναι μεσοκάθετος του
είναι μεσοκάθετος του  .
. Άρα:
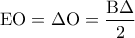
β) Η
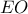 είναι διάμεσος του τριγώνου
είναι διάμεσος του τριγώνου  και είναι ίση με το μισό της
και είναι ίση με το μισό της  . Άρα η γωνία
. Άρα η γωνία  είναι ορθή.
είναι ορθή.γ)
 (είναι κάθετες στην ίδια ευθεία
(είναι κάθετες στην ίδια ευθεία  )
) (απέναντι πλευρές παραλληλογράμμου) και
(απέναντι πλευρές παραλληλογράμμου) και 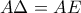 (
( είναι σημείο της μεσοκαθέτου του τμήματος
είναι σημείο της μεσοκαθέτου του τμήματος  )
)Άρα, το τετράπλευρο
 είναι ισοσκελές τραπέζιο ή παραλληλόγραμμο.
είναι ισοσκελές τραπέζιο ή παραλληλόγραμμο.Αν
 (δηλαδή τα σημεία
(δηλαδή τα σημεία  συμπίπτουν), τότε
συμπίπτουν), τότε  , οπότε το
, οπότε το  θα είναι ορθογώνιο.
θα είναι ορθογώνιο.Πιστεύω πως έπρεπε να δοθεί στην εκφώνηση ότι η διαγώνιος
 δεν είναι κάθετη στην πλευρά
δεν είναι κάθετη στην πλευρά  του παραλληλογράμμου. Δηλαδή το (γ) ερώτημα δεν ισχύει για οποιοδήποτε παραλληλόγραμμο
του παραλληλογράμμου. Δηλαδή το (γ) ερώτημα δεν ισχύει για οποιοδήποτε παραλληλόγραμμο  .
.Παρατήρηση: Έχω τη γνώμη ότι το ερώτημα (γ) είναι προβληματικό, για τους λόγους που προανέφερα στη λύση.

 με
με 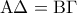 . Αν
. Αν  είναι τα μέσα των
είναι τα μέσα των 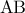 ,
,  και
και  αντίστοιχα, να αποδείξετε ότι:
αντίστοιχα, να αποδείξετε ότι:  ρόμβος.
ρόμβος.  είναι μεσοκάθετος του ευθύγραμμου τμήματος
είναι μεσοκάθετος του ευθύγραμμου τμήματος  .
. 
 διέρχονται από ίδιο σημείο.
διέρχονται από ίδιο σημείο.  αφού το
αφού το  ενώνει τα μέσα δύο πλευρών του τριγώνου
ενώνει τα μέσα δύο πλευρών του τριγώνου 
 αφού το
αφού το  ενώνει τα μέσα δύο πλευρών του τριγώνου
ενώνει τα μέσα δύο πλευρών του τριγώνου 

 συμπεραίνουμε ότι το
συμπεραίνουμε ότι το 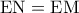 και
και 
 ισαπέχουν από τα άκρα του
ισαπέχουν από τα άκρα του  και
και  γιατί τα
γιατί τα  ενώνουν τα μέσα δύο πλευρών των τριγώνων
ενώνουν τα μέσα δύο πλευρών των τριγώνων 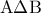 και
και  αντίστοιχα.
αντίστοιχα. είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. και
και  της
της  ,
,  εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο 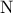 . Μια ευθεία
. Μια ευθεία  εφάπτεται στους δύο κύκλους στα σημεία
εφάπτεται στους δύο κύκλους στα σημεία  αντίστοιχα.
αντίστοιχα.  .
.  . (Μονάδες 7)
. (Μονάδες 7)  (Μονάδες 9)
(Μονάδες 9) (Μονάδες 9)
(Μονάδες 9)
 , οπότε
, οπότε  άρα το
άρα το  ως διχοτόμοι των εφεξής παραπληρωματικών γωνιών
ως διχοτόμοι των εφεξής παραπληρωματικών γωνιών  , είναι μεταξύ τους κάθετες και το ζητούμενο έπεται .
, είναι μεταξύ τους κάθετες και το ζητούμενο έπεται . , έχουμε ότι
, έχουμε ότι 
 είναι χορδής και εφαπτομένης
είναι χορδής και εφαπτομένης  είναι εγγράψιμα , κτλ
είναι εγγράψιμα , κτλ και
και  το μέσον του τόξου του
το μέσον του τόξου του  .
.  εφάπτεται στο κύκλο στο
εφάπτεται στο κύκλο στο  τέμνουν την ευθεία
τέμνουν την ευθεία  και
και  αντίστοιχα .
αντίστοιχα . 

 μέσον της
μέσον της 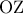
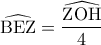
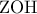
 είναι και απόστημα της χορδής
είναι και απόστημα της χορδής 
 και
και  είναι ίσα επειδή έχουν:
είναι ίσα επειδή έχουν: ως επίκεντρες που βαίνουν στα ίσα τόξα
ως επίκεντρες που βαίνουν στα ίσα τόξα  και
και 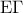 άρα
άρα  είναι ισοσκελές οπότε
είναι ισοσκελές οπότε 
 είναι διάμεσος στην υποτείνουσα, δηλαδή
είναι διάμεσος στην υποτείνουσα, δηλαδή  .
.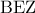 είναι ισοσκελές με
είναι ισοσκελές με  και
και  είναι γωνία χορδής
είναι γωνία χορδής  και εφαπτομένης
και εφαπτομένης  ,
, 



 συνευθειακά σημεία με
συνευθειακά σημεία με  . Θεωρούμε το μέσο
. Θεωρούμε το μέσο  της
της  . Προς το ίδιο ημιεπίπεδο κατασκευάζουμε τα ισόπλευρα τρίγωνα
. Προς το ίδιο ημιεπίπεδο κατασκευάζουμε τα ισόπλευρα τρίγωνα  . Να αποδείξετε ότι:
. Να αποδείξετε ότι: είναι τραπέζιο (
είναι τραπέζιο ( ). (Μονάδες 9)
). (Μονάδες 9) είναι ίσα. (Μονάδες 8)
είναι ίσα. (Μονάδες 8) είναι εγγράψιμο. (Μονάδες 8)
είναι εγγράψιμο. (Μονάδες 8) . Άρα
. Άρα  κι επειδή είναι εντός εναλλάξ,
κι επειδή είναι εντός εναλλάξ,  ), οπότε το τετράπλευρο
), οπότε το τετράπλευρο 
 και
και  . Άρα είναι ίσα.
. Άρα είναι ίσα. (στο ισόπλευρο τρίγωνο κάθε διάμεσος είναι και ύψος). Το τετράπλευρο
(στο ισόπλευρο τρίγωνο κάθε διάμεσος είναι και ύψος). Το τετράπλευρο  της πλευράς
της πλευράς  και
και  κάθετος από τη κορυφή
κάθετος από τη κορυφή  στην ευθεία
στην ευθεία 
 .
.  τέμνει τις
τέμνει τις  αντίστοιχα.
αντίστοιχα.  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. 
 και
και  , οπότε το
, οπότε το  δηλαδή το
δηλαδή το  είναι μέσο του
είναι μέσο του 
 άρα το
άρα το  και
και  άρα και
άρα και 
 το
το  είναι ύψος και διάμεσος οπότε είναι ισοσκελές, δηλαδή
είναι ύψος και διάμεσος οπότε είναι ισοσκελές, δηλαδή  . Κατασκευάζουμε εξωτερικά του τριγώνου τα
. Κατασκευάζουμε εξωτερικά του τριγώνου τα ,
,  . Ονομάζουμε
. Ονομάζουμε  το σημείο τομής των ευθυγράμμων
το σημείο τομής των ευθυγράμμων .
.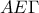 και
και  είναι ίσα και να γράψετε τα ζεύγη των ίσων γωνιών (Μονάδες 10)
είναι ίσα και να γράψετε τα ζεύγη των ίσων γωνιών (Μονάδες 10) ,
, 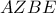 είναι εγγράψιμα. (Μονάδες 10)
είναι εγγράψιμα. (Μονάδες 10)  είναι
είναι  . (Μονάδες 5)
. (Μονάδες 5) .
. .
. και
και  .
. φαίνεται από τις απέναντι κορυφές υπο ίση γωνία).
φαίνεται από τις απέναντι κορυφές υπο ίση γωνία). (ίση με απέναντι εσωτερική).
(ίση με απέναντι εσωτερική). . Συνεπώς
. Συνεπώς  .
. τα ύψη από τις κορυφές
τα ύψη από τις κορυφές  αντίστοιχα και
αντίστοιχα και το ορθόκεντρο του τριγώνου. Επίσης δίνονται τα
το ορθόκεντρο του τριγώνου. Επίσης δίνονται τα  μέσα των
μέσα των αντίστοιχα.
αντίστοιχα. (Μονάδες 6)
(Μονάδες 6)  (Μονάδες 6)
(Μονάδες 6)  είναι ορθογώνιο. (Μονάδες 6)
είναι ορθογώνιο. (Μονάδες 6) , να αποδείξετε ότι
, να αποδείξετε ότι  . (Μονάδες 7)
. (Μονάδες 7) ,
, 
 έχω:
έχω: ,
,  ,
,  ,
,  ,
,  .
. .
. .
. το τετράπλευρο
το τετράπλευρο  . Όμως
. Όμως 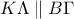 .
. . Είναι
. Είναι  , συνεπώς
, συνεπώς  .
. 
 ορθόκεντρο
ορθόκεντρο  και ισχύουν οι
και ισχύουν οι  έχω
έχω  δηλαδή
δηλαδή  (όπως β. iii) ή γωνίες με πλευρές κάθετες).
(όπως β. iii) ή γωνίες με πλευρές κάθετες). και
και  σημεία των ημιευθειών
σημεία των ημιευθειών  αντίστοιχα, με
αντίστοιχα, με  . Η
. Η  είναι ευθεία που διέρχεται από την κορυφή
είναι ευθεία που διέρχεται από την κορυφή  στο ίδιο ημιεπίπεδο. Η κάθετη από το σημείο
στο ίδιο ημιεπίπεδο. Η κάθετη από το σημείο  στην
στην  και
και  είναι ίσα. (Μονάδες 7)
είναι ίσα. (Μονάδες 7) (Μονάδες 7)
(Μονάδες 7) , όπου
, όπου  είναι το ευθύγραμμο τμήμα που ενώνει τα μέσα των
είναι το ευθύγραμμο τμήμα που ενώνει τα μέσα των  είναι ορθογώνιο και ισοσκελές. (Μονάδες 4)
είναι ορθογώνιο και ισοσκελές. (Μονάδες 4) (είναι οξείες και έχουν τις πλευρές τους κάθετες). Άρα τα τρίγωνα είναι ίσα.
(είναι οξείες και έχουν τις πλευρές τους κάθετες). Άρα τα τρίγωνα είναι ίσα. και
και  .
. είναι διάμεσος του τραπεζίου
είναι διάμεσος του τραπεζίου 
 , τότε το
, τότε το 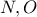 συμπίπτουν και είναι
συμπίπτουν και είναι  . Τότε όμως το τετράπλευρο
. Τότε όμως το τετράπλευρο  είναι τετράγωνο, οπότε
είναι τετράγωνο, οπότε 
 . Έστω
. Έστω  και
και  .
.  (Μονάδες 10)
(Μονάδες 10) (Μονάδες 10)
(Μονάδες 10)  είναι εγγράψιμο. Να αιτιολογήσετε την απάντηση σας. (Μονάδες 5)
είναι εγγράψιμο. Να αιτιολογήσετε την απάντηση σας. (Μονάδες 5) και
και 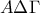 είναι ίσα (κριτήριο ΠΓΠ) γιατί έχουν:
είναι ίσα (κριτήριο ΠΓΠ) γιατί έχουν: (υπόθεση),
(υπόθεση),  και
και  .
. δηλ. το i. και
δηλ. το i. και  .
. .
. ,
, 
 ως κατακορυφήν.
ως κατακορυφήν. και
και  είναι απέναντι γωνίες του, άρα είναι εγγράψιμο.
είναι απέναντι γωνίες του, άρα είναι εγγράψιμο. , τότε
, τότε  και
και  τετράγωνα. Οπότε
τετράγωνα. Οπότε 
 . Στη διαγώνιο
. Στη διαγώνιο 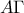 θεωρουμε σημεία
θεωρουμε σημεία  ώστε
ώστε 
 και
και  τα μέσα των πλευρών
τα μέσα των πλευρών  ,
,  και
και  αντίστοιχα ,να αποδείξετε ότι:
αντίστοιχα ,να αποδείξετε ότι:  είναι τετράγωνο.
είναι τετράγωνο. 
 είναι ορθογώνιο παραλληλόγραμμο, με
είναι ορθογώνιο παραλληλόγραμμο, με 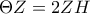
 η
η  ενώνει τα μέσα δύο πλευρών του. Άρα
ενώνει τα μέσα δύο πλευρών του. Άρα  . Eπίσης
. Eπίσης  (διότι το
(διότι το  είναι μέσον του
είναι μέσον του  και συνεπώς το τεράπλευρο
και συνεπώς το τεράπλευρο  είναι ορθή, άρα είναι
είναι ορθή, άρα είναι  . Άρα το πιο πάνω ορθογώνιο, είναι τετράγωνο, αφού έχει δύο διαδοχικές
. Άρα το πιο πάνω ορθογώνιο, είναι τετράγωνο, αφού έχει δύο διαδοχικές  , η
, η  είναι διάμεσος στην υποτείνουσα. Άρα
είναι διάμεσος στην υποτείνουσα. Άρα 
 .
. , η
, η  ενώνει τα μέσα δύο πλευρών του. Άρα
ενώνει τα μέσα δύο πλευρών του. Άρα  . Όμως
. Όμως 
 και άρα το τετράπλευρο
και άρα το τετράπλευρο  του
του είναι το μέσον της μιας διαγωνίου του άρα θα είναι το κέντρο του τετραγώνου και άρα και η άλλη διαγώνιος θα
είναι το μέσον της μιας διαγωνίου του άρα θα είναι το κέντρο του τετραγώνου και άρα και η άλλη διαγώνιος θα 
 και άρα η
και άρα η 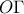 και άρα το παραλληλόγραμμο
και άρα το παραλληλόγραμμο 
 (ως απέναντι πλευρές παραλληλογράμμου) : Όμως
(ως απέναντι πλευρές παραλληλογράμμου) : Όμως 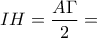
 (διότι από το (β) ερώτημα είδαμε ότι
(διότι από το (β) ερώτημα είδαμε ότι  ). Συμπεραίνουμε λοιπόν ότι
). Συμπεραίνουμε λοιπόν ότι 
 ), τα μέσα
), τα μέσα  των πλευρών του και το ύψος του
των πλευρών του και το ύψος του  . Έστω
. Έστω 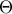 το σημείο τομής των
το σημείο τομής των  είναι ορθογώνιο. (Μονάδες 8)
είναι ορθογώνιο. (Μονάδες 8)  (Μονάδες 7)
(Μονάδες 7) 
 . (Μονάδες 5)
. (Μονάδες 5)  . (Μονάδες 5)
. (Μονάδες 5)  αντίστοιχα, του τριγώνου
αντίστοιχα, του τριγώνου  (διαγώνιοι ορθογωνίου). Οπότε:
(διαγώνιοι ορθογωνίου). Οπότε: . Αλλά
. Αλλά 
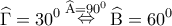
 (διάμεσος ορθογωνίου τριγώνου). Άρα:
(διάμεσος ορθογωνίου τριγώνου). Άρα:  . Δηλαδή το τρίγωνο
. Δηλαδή το τρίγωνο  είναι ισόπλευρο, οπότε
είναι ισόπλευρο, οπότε 

 ισχύει
ισχύει  . Αν η διχοτόμος της γωνίας
. Αν η διχοτόμος της γωνίας  τέμνει την
τέμνει την  στο
στο και την προέκταση της
και την προέκταση της  στο
στο  , να αποδείξετε ότι:
, να αποδείξετε ότι:  είναι ισοσκελές. (Μονάδες 7)
είναι ισοσκελές. (Μονάδες 7) είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας 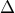 του τραπεζίου. (Μονάδες 8)
του τραπεζίου. (Μονάδες 8) (εντος εναλλάξ) ,έπεται ότι το τρίγωνο
(εντος εναλλάξ) ,έπεται ότι το τρίγωνο 
 είναι παραλληλόγραμμο κι αφού οι διαγώνιες διχοτομούνται , το
είναι παραλληλόγραμμο κι αφού οι διαγώνιες διχοτομούνται , το  , με
, με  και
και  . Θεωρούμε σημείο
. Θεωρούμε σημείο  και
και  . Αν η γωνία
. Αν η γωνία  ,
,  σε συνάρτηση με την
σε συνάρτηση με την 
 σε συνάρτηση με την
σε συνάρτηση με την  και
και  είναι μεσοκάθετοι των τμημάτων
είναι μεσοκάθετοι των τμημάτων  και
και  αντίστοιχα.
αντίστοιχα. είναι ισοσκελές από την υπόθεση και άρα
είναι ισοσκελές από την υπόθεση και άρα  . Από το τρίγωνο
. Από το τρίγωνο 
 είναι και αυτό ισοσκελές από την υπόθεση και άρα
είναι και αυτό ισοσκελές από την υπόθεση και άρα  . Όμως από το τρίγωνο
. Όμως από το τρίγωνο  έχουμε:
έχουμε: , (ΣΧΕΣΗ 1)
, (ΣΧΕΣΗ 1) ( ως εντός και επί τα αυτά μέρη των παραλλήλων
( ως εντός και επί τα αυτά μέρη των παραλλήλων 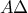 και
και  που τέμνονται από την
που τέμνονται από την  , (ΣΧΕΣΗ 2)
, (ΣΧΕΣΗ 2)
 μέχρι να συναντήσει την ευθεία
μέχρι να συναντήσει την ευθεία 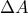 στο σημείο
στο σημείο  . Τότε έχουμε
. Τότε έχουμε  ως κατακορυφήν . Επίσης
ως κατακορυφήν . Επίσης  , ως παρά την βάση γωνίες του ισοσκελούς τριγώνου
, ως παρά την βάση γωνίες του ισοσκελούς τριγώνου  ως εντός εναλλάξ των παραλλήλων
ως εντός εναλλάξ των παραλλήλων 
 που τέμνονται από την
που τέμνονται από την  . Από τα ανωτέρω συμπεραίνουμε ότι
. Από τα ανωτέρω συμπεραίνουμε ότι  και άρα το τρίγωνο
και άρα το τρίγωνο  είναι ισοσκελές , δηλαδή
είναι ισοσκελές , δηλαδή και αφού από την υπόθεση είναι και
και αφού από την υπόθεση είναι και  και συνεπώς το τρίγωνο
και συνεπώς το τρίγωνο  είναι ορθογώνιο με κορυφή
είναι ορθογώνιο με κορυφή , η
, η  ενώνει τα μέσα δύο πλευρών του και άρα θα είναι παράλληλη με την
ενώνει τα μέσα δύο πλευρών του και άρα θα είναι παράλληλη με την  .
. έχουμε ότι η
έχουμε ότι η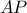 είναι και παράλληλη με την
είναι και παράλληλη με την  , άρα θα περνάει και από το μέσον της
, άρα θα περνάει και από το μέσον της  είναι μεσοκάθετος της
είναι μεσοκάθετος της  , με
, με  .
.  των
των  .
.  (προς το
(προς το  στο σημείο
στο σημείο  .
.  .
. 
 είναι ισοσκελές αφού
είναι ισοσκελές αφού 
 ως εντός και εναλλάξ.
ως εντός και εναλλάξ. οπότε το τρίγωνο
οπότε το τρίγωνο  είναι ισοσκελές με
είναι ισοσκελές με 


 και
και
 , τη γωνία
, τη γωνία  αμβλεία και
αμβλεία και  τέμνει την προέκταση της
τέμνει την προέκταση της  .
.  διχοτομούνται.
διχοτομούνται. 
 και
και  οπότε είναι
οπότε είναι  δηλαδή το τρίγωνο
δηλαδή το τρίγωνο  είναι ισοσκελές οπότε
είναι ισοσκελές οπότε 
 ως εντός και εναλλάξ.
ως εντός και εναλλάξ. δηλαδή η
δηλαδή η  και
και  είναι ίσα από
είναι ίσα από  αφού έχουν:
αφού έχουν: επειδή
επειδή  ως κατακορυφήν και
ως κατακορυφήν και ως εντός και εναλλάξ
ως εντός και εναλλάξ οπότε το
οπότε το  δηλαδή τα
δηλαδή τα  οπότε:
οπότε: δηλαδή το τρίγωνο
δηλαδή το τρίγωνο  είναι ισοσκελές και
είναι ισοσκελές και 
 και
και  κατά τμήμα
κατά τμήμα  .Από το
.Από το 
 αφού
αφού  άρα οι διαγώνιοι του τετραπλέυρου διχοτομούνται και συνεπώς
άρα οι διαγώνιοι του τετραπλέυρου διχοτομούνται και συνεπώς 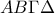 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. είναι
είναι  E και
E και 
 με
με 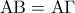 και
και  τα μέσα των πλευρών του
τα μέσα των πλευρών του  (προς το
(προς το  ώστε
ώστε 
 (προς το
(προς το  τέτοιο ώστε
τέτοιο ώστε  .
. 
 και
και  είναι ορθογώνια.
είναι ορθογώνια.  και
και 

 είναι διάμεσος που αντιστοιχεί στην
είναι διάμεσος που αντιστοιχεί στην  , δηλαδή το τρίγωνο είναι ορθογώνιο.
, δηλαδή το τρίγωνο είναι ορθογώνιο. και
και  είναι ίσα από
είναι ίσα από  αφού έχουν:
αφού έχουν: ως μισά των ίσων τμημάτων
ως μισά των ίσων τμημάτων 
 ως αθροίσματα των ίσων τμημάτων
ως αθροίσματα των ίσων τμημάτων  με το
με το  ως γωνίες στη βάση του ισοσκελούς τριγώνου
ως γωνίες στη βάση του ισοσκελούς τριγώνου 

 και
και  , και μια τρίτη που τις τέμνει στα σημεία
, και μια τρίτη που τις τέμνει στα σημεία  είναι ορθή.
είναι ορθή. 

 αφού οι γωνίες
αφού οι γωνίες  είναι παραπληρωματικές ως εντός και επί τα αυτά.
είναι παραπληρωματικές ως εντός και επί τα αυτά.
 είναι διάμεσος στην υποτείνουσα του ορθογωνίου τριγώνου
είναι διάμεσος στην υποτείνουσα του ορθογωνίου τριγώνου  δηλαδή
δηλαδή  και το τρίγωνο
και το τρίγωνο 
 είναι εξωτερική του τριγώνου
είναι εξωτερική του τριγώνου 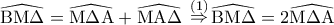
 είναι
είναι  και
και 
