ΑΣΚΗΣΗ 1088
ΕΚΦΩΝΗΣΗ
α) Αν οι αριθμοί

είναι διαδοχικοί όροι αριθμητικής προόδου, να προσδιορίσετε τον αριθμό

.
β) Αν οι αριθμοί

είναι διαδοχικοί όροι γεωμετρικής προόδου, να προσδιορίσετε τον αριθμό

.
γ) Να βρεθεί ο αριθμός

ώστε οι αριθμοί

να είναι διαδοχικοί όροι αριθμητικής και γεωμετρικής προόδου.
Προτεινόμενη λύση
α) Οι αριθμοί

είναι διαδοχικοί όροι αριθμητικής προόδου, και συνεπώς ο

είναι ο αριθμητικός μέσος των

και

. Έχουμε λοιπόν:

.
β) Οι αριθμοί

είναι διαδοχικοί όροι γεωμετρικής προόδου και συνεπώς ισχύει:

. Το τριώνυμο έχει
διακρίνουσα

και συνεπώς έχει δύο άνισες πραγματικές ρίζες, τις:

γ) Λόγω των δύο πρώτων ερωτημάτων έχουμε ότι:
• Οι αριθμοί

είναι διαδοχικοί όροι αριθμητικής προόδου για

, ενώ
• είναι διαδοχικοί όροι γεωμετρικής προόδου για

και

.
Επαλήθευση:
Για

οι τρεις αριθμοί είναι οι

και αποτελούν διαδοχικούς όρους αριθμητικής προόδου με διαφορά

και γεωμετρικής με λόγο

.
 ισχύει:
ισχύει: 
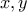 είναι τα μήκη των πλευρών ενός ορθογωνίου παραλληλογράμμου, με
είναι τα μήκη των πλευρών ενός ορθογωνίου παραλληλογράμμου, με  και
και  , τότε να βρείτε τα όρια μεταξύ των οποίων περιέχεται η τιμή του εμβαδού
, τότε να βρείτε τα όρια μεταξύ των οποίων περιέχεται η τιμή του εμβαδού  του ορθογωνίου.
του ορθογωνίου.
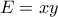 .
.  και
και  και όλα τα μέλη είναι θετικά, πολλαπλασιάζοντας κατά μέλη τις δύο σχέσεις έχουμε:
και όλα τα μέλη είναι θετικά, πολλαπλασιάζοντας κατά μέλη τις δύο σχέσεις έχουμε: .
.
 για την οποία ισχύει ότι:
για την οποία ισχύει ότι:  και
και  .
.

 πρώτων όρων της προόδου.
πρώτων όρων της προόδου. διαδοχικά για
διαδοχικά για  και
και  .
.



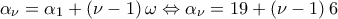 . Συνεπώς για
. Συνεπώς για  έχουμε:
έχουμε: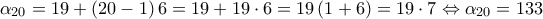 .
. για
για 

 .
. ;
; και συνεπώς το τριώνυμο έχει δύο άνισες πραγματικές ρίζες, τις:
και συνεπώς το τριώνυμο έχει δύο άνισες πραγματικές ρίζες, τις: .
. 
 για τα οποία ο παρονομαστής της παραμένει διάφορος του μηδενός. Οι ρίζες του παρονομαστή, είναι οι ρίζες του τριωνύμου του πρώτου ερωτήματος, δηλαδή οι
για τα οποία ο παρονομαστής της παραμένει διάφορος του μηδενός. Οι ρίζες του παρονομαστή, είναι οι ρίζες του τριωνύμου του πρώτου ερωτήματος, δηλαδή οι  και
και  .
. .
.
 με
με  και
και  ώστε να ισχύουν:
ώστε να ισχύουν: και
και  .
. και
και  .
.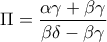
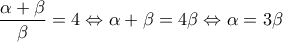 και
και 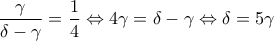 .
. .
. , όπου
, όπου  είναι η περίμετρος του ορθογωνίου.
είναι η περίμετρος του ορθογωνίου. .
. 
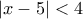 .
. επαληθεύει την παραπάνω ανίσωση, να αποδείξετε ότι:
επαληθεύει την παραπάνω ανίσωση, να αποδείξετε ότι:

 .
. 
 .
. .
.
 . Τότε:
. Τότε: 

 .
. .
. .
. . Η διακρίνουσα του τριωνύμου είναι
. Η διακρίνουσα του τριωνύμου είναι  και συνεπώς
και συνεπώς . Συνεπώς το πεδίο ορισμού της
. Συνεπώς το πεδίο ορισμού της  .
. η συνάρτηση απλοποιείται και γράφεται:
η συνάρτηση απλοποιείται και γράφεται:  . Τότε
. Τότε  .
. ,
,  ,
,  είναι, με τη σειρά που δίνονται, διαδοχικοί όροι αριθμητικής προόδου
είναι, με τη σειρά που δίνονται, διαδοχικοί όροι αριθμητικής προόδου  .
. και ο αριθμός
και ο αριθμός  είναι ο πρώτος όρος της αριθμητικής προόδου
είναι ο πρώτος όρος της αριθμητικής προόδου  .
. αποτελούν διαδοχικούς όρους αριθμητικής προόδου και συνεπώς ο
αποτελούν διαδοχικούς όρους αριθμητικής προόδου και συνεπώς ο 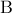 είναι ο αριθμητικός μέσος των
είναι ο αριθμητικός μέσος των  και
και  . Ισχύει λοιπόν:
. Ισχύει λοιπόν:
 και
και  .
. .
. και
και  , ο νιοστός όρος δίνεται από τον τύπο
, ο νιοστός όρος δίνεται από τον τύπο 
 . Οπότε για
. Οπότε για  .
. είναι διαδοχικοί όροι αριθμητικής προόδου, να προσδιορίσετε τον αριθμό
είναι διαδοχικοί όροι αριθμητικής προόδου, να προσδιορίσετε τον αριθμό  και
και  . Έχουμε λοιπόν:
. Έχουμε λοιπόν:  .
. . Το τριώνυμο έχει
. Το τριώνυμο έχει  και συνεπώς έχει δύο άνισες πραγματικές ρίζες, τις:
και συνεπώς έχει δύο άνισες πραγματικές ρίζες, τις: 
 , ενώ
, ενώ .
. και αποτελούν διαδοχικούς όρους αριθμητικής προόδου με διαφορά
και αποτελούν διαδοχικούς όρους αριθμητικής προόδου με διαφορά  και γεωμετρικής με λόγο
και γεωμετρικής με λόγο  .
.