Θεωρούμε τις συναρτήσεις
 και
και  , με
, με  και
και  .
. α) Για
 , να προσδιορίσετε τα κοινά σημεία των γραφικών παραστάσεων των συναρτήσεων
, να προσδιορίσετε τα κοινά σημεία των γραφικών παραστάσεων των συναρτήσεων  και
και  .
.β) Να βρείτε για ποιες τιμές του
 οι γραφικές παραστάσεις των συναρτήσεων
οι γραφικές παραστάσεις των συναρτήσεων  και
και  τέμνονται σε δύο σημεία .
τέμνονται σε δύο σημεία .γ) Για
 , να εξετάσετε αν οι τετμημένες των σημείων τομής των γραφικών παραστάσεων των συναρτήσεων
, να εξετάσετε αν οι τετμημένες των σημείων τομής των γραφικών παραστάσεων των συναρτήσεων  και
και  είναι ομόσημες ή ετερόσημες .
είναι ομόσημες ή ετερόσημες .Ενδεικτικές απαντήσεις :
α) Για
 , ο τύπος της συνάρτησης
, ο τύπος της συνάρτησης  είναι
είναι  . Τα σημεία τομής των γραφικών παραστάσεων των συναρτήσεων
. Τα σημεία τομής των γραφικών παραστάσεων των συναρτήσεων  και
και  είναι οι λύσεις του συστήματος :
είναι οι λύσεις του συστήματος :  και
και  (1).
(1). Επομένως από το σύστημα παίρνουμε
 (2) .
(2) . Οπότε για
 σε μια από τις δύο εξισώσεις του συστήματος (1) έχω
σε μια από τις δύο εξισώσεις του συστήματος (1) έχω  ,
, ενώ για
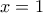 σε μια από τις δύο εξισώσεις του συστήματος (1) έχω
σε μια από τις δύο εξισώσεις του συστήματος (1) έχω  . Άρα τα κοινά σημεία των γραφικών παραστάσεων των συναρτήσεων
. Άρα τα κοινά σημεία των γραφικών παραστάσεων των συναρτήσεων  και
και  είναι τα
είναι τα  και
και  .
. β) Για να τέμνονται σε δύο σημεία οι γραφικές παραστάσεις των συναρτήσεων
 και
και  θα πρέπει το σύστημα :
θα πρέπει το σύστημα :  και
και  (1) να έχει δύο λύσεις .
(1) να έχει δύο λύσεις . Επομένως από το σύστημα παίρνουμε
 (2) .
(2) . Πρέπει για την δευτεροβάθμια εξίσωση που προέκυψε να έχω :
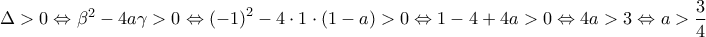
γ) Για
 .
.Όμως στην δευτεροβάθμια εξίσωση
 είναι
είναι  (όπου
(όπου  , το γινόμενο των ριζών της δευτεροβάθμιας εξίσωσης).
, το γινόμενο των ριζών της δευτεροβάθμιας εξίσωσης).Επειδή
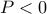 οι τετμημένες των σημείων τομής των γραφικών παραστάσεων των συναρτήσεων
οι τετμημένες των σημείων τομής των γραφικών παραστάσεων των συναρτήσεων  και
και  είναι ετερόσημες .
είναι ετερόσημες .
 και
και  ,
,  ακέραιος με
ακέραιος με  .
.  της προόδου είναι αριθμός περιττός .
της προόδου είναι αριθμός περιττός . , τότε :
, τότε :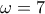 .
. είναι όρος της προόδου .
είναι όρος της προόδου . .
.  , άρα
, άρα  (1) και
(1) και  (2) .
(2) . .
.
 , άρα
, άρα  δεκτή , αφού
δεκτή , αφού  , περιττός και
, περιττός και  , απορρίπτεται αφού
, απορρίπτεται αφού  .
. είναι
είναι  .
. ώστε
ώστε  .
. .
. .
. .
.
 που ικανοποιούν την ανίσωση
που ικανοποιούν την ανίσωση 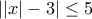 .
. .
. .
. .
.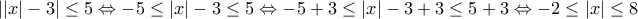
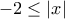 που ισχύει για κάθε πραγματικό αριθμό
που ισχύει για κάθε πραγματικό αριθμό 
 , επομένως το πλήθος των ακεραίων είναι
, επομένως το πλήθος των ακεραίων είναι  .
. , με παράμετρο
, με παράμετρο  ,
,  , για κάθε
, για κάθε  .
.  (1) . Άρα για να έχει η δοθείσα εξίσωση δυο ρίζες πραγματικές και άνισες πρέπει η (1) να έχει θετική διακρίνουσα .
(1) . Άρα για να έχει η δοθείσα εξίσωση δυο ρίζες πραγματικές και άνισες πρέπει η (1) να έχει θετική διακρίνουσα .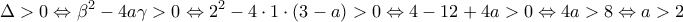 .
. .
.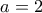 η (1) γίνεται
η (1) γίνεται  , ηδιπλή ρίζα της εξίσωσης .
, ηδιπλή ρίζα της εξίσωσης .  .
.

 .
. ,
,  .
.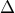 του τριωνύμου και να αποδείξετε ότι το τριώνυμο έχει ρίζες πραγματικές για κάθε
του τριωνύμου και να αποδείξετε ότι το τριώνυμο έχει ρίζες πραγματικές για κάθε  ,
,  είναι οι ρίζες του τριωνύμου , να εκφράσετε το άθροισμα
είναι οι ρίζες του τριωνύμου , να εκφράσετε το άθροισμα  συναρτήσει του
συναρτήσει του  και να βρείτε την τιμή του γινομένου
και να βρείτε την τιμή του γινομένου  , το παραπάνω τριώνυμο έχει ρίζες θετικές ή αρνητικές ; Να αιτιολογήσετε την απάντηση σας .
, το παραπάνω τριώνυμο έχει ρίζες θετικές ή αρνητικές ; Να αιτιολογήσετε την απάντηση σας . .
.![\displaystyle{\Delta ={{\beta }^{2}}-4a\gamma \Leftrightarrow \Delta ={{\left[ -\left( {{\lambda }^{2}}+1 \right) \right]}^{2}}-4\cdot \lambda \cdot \lambda \Leftrightarrow \Delta ={{\left( {{\lambda }^{2}}+1 \right)}^{2}}-4{{\lambda }^{2}}\Leftrightarrow \Delta ={{\lambda }^{4}}+2{{\lambda }^{2}}+1-4{{\lambda }^{2}}\Leftrightarrow } \displaystyle{\Delta ={{\beta }^{2}}-4a\gamma \Leftrightarrow \Delta ={{\left[ -\left( {{\lambda }^{2}}+1 \right) \right]}^{2}}-4\cdot \lambda \cdot \lambda \Leftrightarrow \Delta ={{\left( {{\lambda }^{2}}+1 \right)}^{2}}-4{{\lambda }^{2}}\Leftrightarrow \Delta ={{\lambda }^{4}}+2{{\lambda }^{2}}+1-4{{\lambda }^{2}}\Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/ef56bc7108834be67d657142458a948f.png)
 , για κάθε
, για κάθε  και
και 
 και
και  , οπότε έχει ρίζες θετικές .
, οπότε έχει ρίζες θετικές . ,επειδή
,επειδή  , ισοδύναμα έχω
, ισοδύναμα έχω 
 , που ισχύει για κάθε
, που ισχύει για κάθε  και
και  και 1 .
και 1 .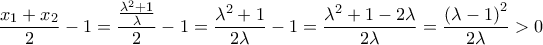 , για κάθε
, για κάθε  .
. είναι οι ρίζες του παραπάνω τριωνύμου , τότε να βρείτε το πρόσημο του γινομένου
είναι οι ρίζες του παραπάνω τριωνύμου , τότε να βρείτε το πρόσημο του γινομένου  , όπου
, όπου  είναι αριθμοί τέτοιοι ώστε
είναι αριθμοί τέτοιοι ώστε  .
.
 ,
,  και
και  επομένως
επομένως 

 (Μονάδες 10)
(Μονάδες 10) οι οποίοι είναι λύσεις της ανίσωσης
οι οποίοι είναι λύσεις της ανίσωσης 

 είναι μεταξύ των
είναι μεταξύ των 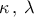 (Μονάδες 8)
(Μονάδες 8) (Μονάδες 7)
(Μονάδες 7)
 , οπότε :
, οπότε : 

 είναι ετερόσημοι , άρα :
είναι ετερόσημοι , άρα : ή
ή 
 θα ανήκουν στο σύνολο
θα ανήκουν στο σύνολο ![\displaystyle{\,( - \infty ,\frac{1}{2}] \cup [2, + \infty )\,\,\,} \displaystyle{\,( - \infty ,\frac{1}{2}] \cup [2, + \infty )\,\,\,}](/forum/ext/geomar/texintegr/latexrender/pictures/c7c015f881ca01d4da25ac1f3bb14d9b.png)
 , δεν βρίσκονται συγχρόνως στο ίδιο διάστημα .
, δεν βρίσκονται συγχρόνως στο ίδιο διάστημα . , η μεταξύ τους απόσταση δεν μπορεί να είναι μικρότερη του
, η μεταξύ τους απόσταση δεν μπορεί να είναι μικρότερη του 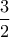 , που
, που  , μπορούμε να υποθέσουμε ότι
, μπορούμε να υποθέσουμε ότι  .
. , οπότε
, οπότε  και με πρόσθεση κατά μέλη :
και με πρόσθεση κατά μέλη : , αφού
, αφού 

 ,
, είναι οι ρίζες θα έχουμε ότι:
είναι οι ρίζες θα έχουμε ότι:
 .
.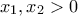 ,
,  ,
, 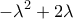

 .
. έχουμε:
έχουμε: .
. .
.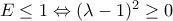 , η οποία ισχύει, άρα ισχύει και η αρχική.
, η οποία ισχύει, άρα ισχύει και η αρχική. .
. η εξίσωση γίνεται:
η εξίσωση γίνεται:  ,
, ,
,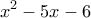

 .
. .
. με
με  , οπότε
, οπότε  .
. και
και 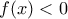 , για κάθε
, για κάθε  ,
, .
. .
. , αφού
, αφού  .
. και
και
 ,
, .
. έχουμε:
έχουμε: , η οποία ισχύει, άρα και η αρχική.
, η οποία ισχύει, άρα και η αρχική. .
. έχουμε
έχουμε  , οπότε το ορθογώνιο τρίγωνο είναι και ισοσκελές.
, οπότε το ορθογώνιο τρίγωνο είναι και ισοσκελές.
 .
. .
. .
. έχουμε:
έχουμε:  , η οποία ισχύει, άρα και η αρχική.
, η οποία ισχύει, άρα και η αρχική. ,
, βρίσκεται στο μέσο της πλευράς
βρίσκεται στο μέσο της πλευράς 

 .
.
 .
. μήκη και
μήκη και  εμβαδό, έχουμε ότι
εμβαδό, έχουμε ότι  .
. .
.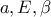 είναι διαδοχικοί όροι γεωμετρικής προόδου ισχύει
είναι διαδοχικοί όροι γεωμετρικής προόδου ισχύει .
. βρίσκουμε ότι:
βρίσκουμε ότι:  , λόγω της
, λόγω της  .
. .
. , όπου
, όπου  .
. έχουμε
έχουμε 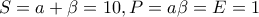
 .
. είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης  ,
, ή
ή  .
. είναι διαδοχικοί όροι αριθμητικής προόδου, αν και μόνο αν
είναι διαδοχικοί όροι αριθμητικής προόδου, αν και μόνο αν 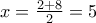 .
. .
. .
. .
. είναι αριθμητική πρόοδος με
είναι αριθμητική πρόοδος με  και
και  , οπότε:
, οπότε: .
. είναι γεωμετρική πρόοδος με
είναι γεωμετρική πρόοδος με  και
και  , οπότε:
, οπότε: .
. έτσι ώστε:
έτσι ώστε:  , οπότε
, οπότε , αφού η ρίζα
, αφού η ρίζα  (απορρίπτεται).
(απορρίπτεται). έχει διακρίνουσα
έχει διακρίνουσα  .
. .
. .
. , οπότε
, οπότε  και
και  , άρα το τριώνυμο έχει δύο άνισες πραγματικές ρίζες (
, άρα το τριώνυμο έχει δύο άνισες πραγματικές ρίζες ( ).
). , προκύπτει ότι οι ρίζες είναι θετικές.
, προκύπτει ότι οι ρίζες είναι θετικές. .
.
 έχει δύο άνισες πραγματικές και θετικές ρίζες, οπότε αρκεί να ισχύει
έχει δύο άνισες πραγματικές και θετικές ρίζες, οπότε αρκεί να ισχύει  .
. έχουμε ότι
έχουμε ότι  .
.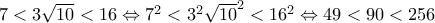 , η οποία ισχύει άρα και η αρχική.
, η οποία ισχύει άρα και η αρχική. έχει τέσσερις διαφορετικές και πραγματικές ρίζες.
έχει τέσσερις διαφορετικές και πραγματικές ρίζες. με
με  .
. με
με  .
. .
.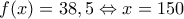
 .
. , έχουμε:
, έχουμε: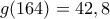 ,
, να ανήκει στον άνδρα με ύψος περίπου
να ανήκει στον άνδρα με ύψος περίπου  έτσι ώστε:
έτσι ώστε: .
.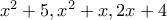 είναι διαδοχικοί όροι αριθμητικής προόδου, αν και μόνο αν ισχύει
είναι διαδοχικοί όροι αριθμητικής προόδου, αν και μόνο αν ισχύει  .
. οι τρεις διαδοχικοί όροι είναι οι
οι τρεις διαδοχικοί όροι είναι οι  , οπότε η διαφορά της προόδου είναι
, οπότε η διαφορά της προόδου είναι  .
.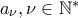 είναι η αριθμητική πρόοδος με
είναι η αριθμητική πρόοδος με  , έχουμε
, έχουμε  .
. .
. πρώτων όρων της αριθμητικής προόδου, είναι:
πρώτων όρων της αριθμητικής προόδου, είναι: .
. .
. είναι η αριθμητική πρόοδος με διαφορά
είναι η αριθμητική πρόοδος με διαφορά  και πρώτο όρο
και πρώτο όρο  .
. .
. .
. .
. .
. έτσι ώστε:
έτσι ώστε: ,
, έχουν μοναδικό κοινό σημείο το
έχουν μοναδικό κοινό σημείο το  , αφού
, αφού  .
. .
. έχει διακρίνουσα
έχει διακρίνουσα  .
. , τότε
, τότε  , οπότε η εξίσωση
, οπότε η εξίσωση  , τότε
, τότε  , οπότε η εξίσωση
, οπότε η εξίσωση