[9] Έστω
 τα σημεία τομής της ευθείας
τα σημεία τομής της ευθείας  με τις γραφικές παραστάσεις των συναρτήσεων
με τις γραφικές παραστάσεις των συναρτήσεων αντίστοχα.
αντίστοχα.Αν
 , ποια η τιμή της σταθεράς
, ποια η τιμή της σταθεράς  ;
;[10] Για την κυβική (πολυώνυμο τρίτου βαθμού) συνάρτηση
 η εφαπτομένη της καμπύλης
η εφαπτομένη της καμπύλης 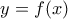 στο σημείο της
στο σημείο της  , συμπίπτει με την εφαπτομένη της καμπύλης
, συμπίπτει με την εφαπτομένη της καμπύλης  στο σημείο της
στο σημείο της  . Ποια η τιμή της
. Ποια η τιμή της  ;
; [11] Δίνεται η συνάρτηση
 ορισμένη στο σύνολο
ορισμένη στο σύνολο  , όπου
, όπου  θετικός αριθμός. Καθώς και μια ευθεία που τέμνει την γραφική παράσταση
θετικός αριθμός. Καθώς και μια ευθεία που τέμνει την γραφική παράσταση 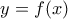 στα σημεία
στα σημεία  όπως φαίνεται στο σχήμα. Έστω
όπως φαίνεται στο σχήμα. Έστω  το σημείο τομής της γραφικής παράστασης της
το σημείο τομής της γραφικής παράστασης της 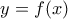 με την παράλληλη ευθεία από το
με την παράλληλη ευθεία από το  προς τον άξονα των
προς τον άξονα των  , διαφορετικό του
, διαφορετικό του  . Αν το τρίγωνο
. Αν το τρίγωνο  είναι ισόπλευρο, πόσο είναι το εμβαδόν του; (Όπου
είναι ισόπλευρο, πόσο είναι το εμβαδόν του; (Όπου  η αρχή των αξόνων.)
η αρχή των αξόνων.)[12] Η συνεχής σε όλους τους πραγματικούς αριθμούς συνάρτηση
 ικανοποιεί την συνθήκη
ικανοποιεί την συνθήκη  για όλους τους πραγματικούς
για όλους τους πραγματικούς  . Αν η μέγιστη τιμή της
. Αν η μέγιστη τιμή της  είναι
είναι  και η ελάχιστη
και η ελάχιστη  , ποιά η τιμή της έκφρασης
, ποιά η τιμή της έκφρασης  ;
;[13] Για δυο σταθερές
 και
και 
 , η ευθεία που διέρχεται από τα σημεία
, η ευθεία που διέρχεται από τα σημεία  ,
,  και η ευθεία που διέρχεται από τα σημεία
και η ευθεία που διέρχεται από τα σημεία  ,
,  στο καρτεσιανό επίπεδο, τέμνουν τον άξονα
στο καρτεσιανό επίπεδο, τέμνουν τον άξονα  στο ίδιο σημείο. Αν για την συνάρτηση
στο ίδιο σημείο. Αν για την συνάρτηση  είναι
είναι  , ποια η τιμή
, ποια η τιμή  ;
;[14] Η τεταγμένη της θέσης ενός κινούμενου σημείου
 την χρονική στιγμή
την χρονική στιγμή  δίνεται από την σχέση
δίνεται από την σχέση  , όπου
, όπου  σταθερές με
σταθερές με  . Αν η ταχύτητα
. Αν η ταχύτητα  του σημείου
του σημείου  την χρονική στιγμή
την χρονική στιγμή  ικανοποιεί την συνθήκη
ικανοποιεί την συνθήκη  , ποιές από τις παρακάτω προτάσεις είναι αληθείς;
, ποιές από τις παρακάτω προτάσεις είναι αληθείς;i)
 .
.ii) Υπάρχει
 που ανήκει στο ανοιχτό διάστημα
που ανήκει στο ανοιχτό διάστημα  για το οποίο
για το οποίο  .
.iii) Αν
 για κάθε
για κάθε  με
με  , τότε υπάρχει
, τότε υπάρχει  του ανοιχτού διαστήματος
του ανοιχτού διαστήματος  , ώστε
, ώστε  .
. [20] Η παραγωγίσημη σε όλους τους πραγματικούς αριθμούς συνάρτηση
 ικανοποιεί τις παρακάτω συνθήκες:
ικανοποιεί τις παρακάτω συνθήκες:Α) Στο κλειστό διάστειμα
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ,
,  .
.Β) Στο διάστημα
 για κάποιους σταθερούς αριθμούς
για κάποιους σταθερούς αριθμούς  ,
,  .
.Να βρείτε την τιμή της έκφρασης
 .
.[21] Η ακολουθία
 ικανοποιεί τις συνθήκες
ικανοποιεί τις συνθήκεςa)

b) Για όλους τους θετικούς ακέραιους
 ,
, 
c)
 .
.Ποιά η τιμή του αθροίσματος
 ;
;[22] (Κοινό θέμα Α & Β ομάδας)
Για ένα πραγματικό αριθμό
 ας είναι
ας είναι  ο αριθμός των πραγματικών ριζών της εξίσωσης
ο αριθμός των πραγματικών ριζών της εξίσωσης  στο κλειστό διάστημα
στο κλειστό διάστημα ![[t, t+2] [t, t+2]](/forum/ext/geomar/texintegr/latexrender/pictures/ea79bf0e5e12b5d899561a165c6b617b.png) , όπου
, όπου  κυβική συνάρτηση με συντελεστή μεγιστοβάθμιου όρου ίσο με
κυβική συνάρτηση με συντελεστή μεγιστοβάθμιου όρου ίσο με 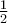 . Η συνάρτηση
. Η συνάρτηση  ικανοποιεί τις παρακάτω συνθήκες:
ικανοποιεί τις παρακάτω συνθήκες:Α) Για κάθε πραγματικό αριθμό
 ,
,  .
.Β)
 .
.Να βρείτε την τιμή
 .
.Edit: 30/11/2021 Έγινε διώρθωση στην εκφώνηση του θέματος [14], ύστερα από παρατήρηση του Χρήστου Ντάβα.

 , βρίσκουμε
, βρίσκουμε  . Αλλά στο
. Αλλά στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/63cf0c477385f522d8da2bcede82265f.png) είναι
είναι  .
.  . Παραγωγίζοντας τώρα την δοθείσα θα βρούμε
. Παραγωγίζοντας τώρα την δοθείσα θα βρούμε , που για
, που για  , δηλαδή
, δηλαδή  .
. . Άρα με αλλαγή μεταβλητής
. Άρα με αλλαγή μεταβλητής  έχουμε
έχουμε  (στην τελευταία ισότητα χρησιμοποίησα το γεγονός ότι για
(στην τελευταία ισότητα χρησιμοποίησα το γεγονός ότι για  ισχύει
ισχύει  ).
). , όπου
, όπου 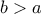 . Tότε
. Tότε  , οπότε
, οπότε  και τελικά
και τελικά  .
.  ισχύει
ισχύει  και
και  , ή αλλιώς
, ή αλλιώς  .
. .
.  , ισοδύναμα
, ισοδύναμα  από όπου
από όπου 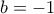 και
και  . Πίσω στη
. Πίσω στη  , βρίσκουμε
, βρίσκουμε  .
. καθορίστηκαν από το γεγονός ότι η συνάρτηση είναι περιττή στο διάστημα
καθορίστηκαν από το γεγονός ότι η συνάρτηση είναι περιττή στο διάστημα  και περιοδική με περίοδο
και περιοδική με περίοδο  (τουλάχιστον αν επεκτείναμε το πεδίο ορισμού της), θεωρήθηκε επίσης ότι
(τουλάχιστον αν επεκτείναμε το πεδίο ορισμού της), θεωρήθηκε επίσης ότι  .
.

 και
και  .
. άρα
άρα 
 θα είχαμε τελικά μια ταυτότητα που για την επίλυση της άσκησης θα ήταν άχρηστη.
θα είχαμε τελικά μια ταυτότητα που για την επίλυση της άσκησης θα ήταν άχρηστη.


 είναι δευτεροβάθμιο πολυώνυμο άρα έχει το πολύ δύο πραγματικές ρίζες. Αφού
είναι δευτεροβάθμιο πολυώνυμο άρα έχει το πολύ δύο πραγματικές ρίζες. Αφού  τότε έχει ακριβώς δύο ρίζες, έστω τις
τότε έχει ακριβώς δύο ρίζες, έστω τις  με
με  . Μάλιστα πρέπει
. Μάλιστα πρέπει  αφού
αφού  .
.  . Πράγματι αν
. Πράγματι αν  με
με  , τότε για
, τότε για  είναι
είναι  και θα έχουμε
και θα έχουμε  άτοπο.
άτοπο. και
και  . Έστω
. Έστω  . Αφού ο συντελεστής μεγιστοβάθμιου όρου του
. Αφού ο συντελεστής μεγιστοβάθμιου όρου του  είναι ίσος με
είναι ίσος με 

 . Αφού
. Αφού  τότε
τότε 
 που δίνει
που δίνει  ή
ή  .
.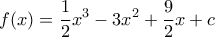 και αφού
και αφού  παίρνουμε
παίρνουμε  . Δηλαδή
. Δηλαδή 
 και στο διάστημα
και στο διάστημα ![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) έχουμε ακριβώς μία ρίζα του
έχουμε ακριβώς μία ρίζα του  και αφού
και αφού  παίρνουμε
παίρνουμε  . Δηλαδή
. Δηλαδή 
 και στο διάστημα
και στο διάστημα ![[-6,-4] [-6,-4]](/forum/ext/geomar/texintegr/latexrender/pictures/bc1815ff61af67477391318bf0f024f0.png) δεν έχουμε καμία ρίζα του
δεν έχουμε καμία ρίζα του  και 4) που απορρίπτεται.
και 4) που απορρίπτεται. .
. ;
; πώς προκύπτει αυτό;
πώς προκύπτει αυτό;
 .
. και
και 






 τότε από την
τότε από την  έχουμε
έχουμε  , μοναδική ρίζα που ταυτίζεται εδώ με το ελάχιστο .
, μοναδική ρίζα που ταυτίζεται εδώ με το ελάχιστο .
 επειδή
επειδή  η παραπάνω δίνει
η παραπάνω δίνει  , λόγω της συνέχειας στο
, λόγω της συνέχειας στο  είναι
είναι 
 τότε για κάθε
τότε για κάθε  θα είναι
θα είναι  .
. όπου
όπου  .
.![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) ή στο
ή στο ![[a,0] [a,0]](/forum/ext/geomar/texintegr/latexrender/pictures/2955b3e7c2e7ee9dc0138db0aadac416.png) έχουμε
έχουμε  και από το θεώρημα Ενδιαμέσων Τιμών προκύπτει ότι
και από το θεώρημα Ενδιαμέσων Τιμών προκύπτει ότι ή
ή  με
με  .
. 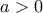 τότε
τότε  , επειδή
, επειδή  ή
ή  σε κάθε περίπτωση άτοπο, ομοίως αν
σε κάθε περίπτωση άτοπο, ομοίως αν  .
. .
.

 (είναι και άσκηση του σχολικού της Άλγεβρας Β' Λυκείου στην παρ. 5.2_6 Β)
(είναι και άσκηση του σχολικού της Άλγεβρας Β' Λυκείου στην παρ. 5.2_6 Β) για τις ευθείες
για τις ευθείες και
και  οι οποίες τέμνονται επί του κατακόρυφου άξονα
οι οποίες τέμνονται επί του κατακόρυφου άξονα 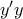

 , τελικά
, τελικά  και
και 





 .Αρκεί να δείξουμε ότι
.Αρκεί να δείξουμε ότι 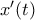 και βλέπουμε ότι έχει μοναδική ρίζα στο
και βλέπουμε ότι έχει μοναδική ρίζα στο  . Άρα η πρόταση είναι αληθής.
. Άρα η πρόταση είναι αληθής.
 . Άρα η πρόταση αυτή είναι ψευδής.
. Άρα η πρόταση αυτή είναι ψευδής. είναι εκτός του διαστήματος
είναι εκτός του διαστήματος  θα μηδενίζεται σε ένα μοναδικό σημείο του διαστήματος
θα μηδενίζεται σε ένα μοναδικό σημείο του διαστήματος  (η
(η  είναι πολυώνυμο τρίτου βαθμού).
είναι πολυώνυμο τρίτου βαθμού). θα αλλάζει πρόσημο. Έστω ότι στο
θα αλλάζει πρόσημο. Έστω ότι στο  είναι θετική και στο
είναι θετική και στο  αρνητική. Τότε θα έχουμε
αρνητική. Τότε θα έχουμε . Άτοπο.
. Άτοπο.  είναι αρνητική στο
είναι αρνητική στο