Παραθέτω τις διάφορες εκδόσεις του 6ου ερωτήματος (απο σύνολο 7, το 7ο ήταν στερεομετρία).
6.1 Να βρείτε την μέγιστη τιμή που μπορεί να πάρει η έκφραση
 , αν είναι γνωστό ότι τα
, αν είναι γνωστό ότι τα  και
και  ικανοποιούν την ισότητα
ικανοποιούν την ισότητα .
.6.2 Να βρείτε όλες τις τιμές της παραμέτρου
 , για τις οποίες η ελάχιστη τιμή (ως προς
, για τις οποίες η ελάχιστη τιμή (ως προς  ) της έκφρασης
) της έκφρασης 
μεγιστοποιείται.
6.3 Να βρείτε όλες τις τιμές της παραμέτρου
 , για τις οποίες η ανίσωση
, για τις οποίες η ανίσωση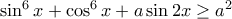
ικανοποιείται για όλους τους πραγματικούς αριθμούς
 .
.6.4 Να βρείτε όλες τις τιμές της παρμαέτρου
 , για τις οποίες η εξίσωση
, για τις οποίες η εξίσωση 
έχει ακριβώς μία λύση.
6.5 Να βρείτε όλα τα ζεύγη πραγματικών αριθμών
 με την ελάχιστη δυνατή τιμή του
με την ελάχιστη δυνατή τιμή του  , που ικανοποιούν την ανίσωση
, που ικανοποιούν την ανίσωση .
.6.6 Να βρείτε όλα τα ζεύγη πραγματικών αριθμών
 , που ικανοποιούν την ισότητα
, που ικανοποιούν την ισότητα .
.
![\displaystyle x,y\in [0,1] \displaystyle x,y\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ce3ec2f825ae4f3dfa7d93837b8bbfe9.png) προκύπτει από τους περιορισμούς των ριζικών
προκύπτει από τους περιορισμούς των ριζικών και εχω
και εχω

 (1)
(1) (2)
(2)![y\in[0,1] y\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5b31148c0673fb11d2612367fae95170.png) η μέγιστη τιμή της παράστασης είναι
η μέγιστη τιμή της παράστασης είναι 
![χ\in[0,1] χ\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d37716c7f28b5cb385782e29a107cb6b.png) η μέγιστη τιμη της παράστασης είναι
η μέγιστη τιμη της παράστασης είναι 