 μπορεί να εκφραστεί με μοναδικό τρόπο ως άθροισμα διακεριμένων προσθετέων της μορφής
μπορεί να εκφραστεί με μοναδικό τρόπο ως άθροισμα διακεριμένων προσθετέων της μορφής  , όπου
, όπου  μη αρνητικός ακέραιος. (Η έκφραση αυτή αναπαριστά την δυαδική μορφή του
μη αρνητικός ακέραιος. (Η έκφραση αυτή αναπαριστά την δυαδική μορφή του  . Σας ζητείτε η απόδειξη της ύπαρξης και μοναδικότητας αυτής της μορφής, δεν επιτρέπεται να τα θεωρήσετε δεδομένα.)
. Σας ζητείτε η απόδειξη της ύπαρξης και μοναδικότητας αυτής της μορφής, δεν επιτρέπεται να τα θεωρήσετε δεδομένα.)(ii) Να αποδείξετε, ότι υπάρχουν άπειροι ακέραιοι
 που μπορούν να γραφούν ως το άθροισμα διακεκριμένων προσθετέων της μορφής
που μπορούν να γραφούν ως το άθροισμα διακεκριμένων προσθετέων της μορφής  όπου
όπου  μη αρνητικός ακέραιος.
μη αρνητικός ακέραιος.(iii) Να αποδείξετε ότι υπάρχουν άπειροι μη αρνητικοί ακέραιοι
 , οι οποίοι δεν μπορούν να εκφραστούν στην μορφή του ερωτήματος (ii).
, οι οποίοι δεν μπορούν να εκφραστούν στην μορφή του ερωτήματος (ii).
 , τότε δεν μπορούμε να γράψουμε ούτε τον αριθμό
, τότε δεν μπορούμε να γράψουμε ούτε τον αριθμό  . Αφού δεν μπορούμε να γράψουμε το
. Αφού δεν μπορούμε να γράψουμε το  τότε δεν θα μπορούμε ούτε τους
τότε δεν θα μπορούμε ούτε τους  .
. , αν θέλουμε να γράψουμε τον
, αν θέλουμε να γράψουμε τον  . (Ασφαλώς δεν μπορούμε να χρησιμοποιήσουμε τον
. (Ασφαλώς δεν μπορούμε να χρησιμοποιήσουμε τον  ή μεγαλύτερο αφού επαγωγικά είναι εύκολο να δειχθεί ότι
ή μεγαλύτερο αφού επαγωγικά είναι εύκολο να δειχθεί ότι  οπότε θα έχουμε
οπότε θα έχουμε  . ) Αν όμως χρησιμοποιήσω τον
. ) Αν όμως χρησιμοποιήσω τον  το πλήθος των ακεραίων στο διάστημα
το πλήθος των ακεραίων στο διάστημα ![[0,n] [0,n]](/forum/ext/geomar/texintegr/latexrender/pictures/f0eb94d54e8e6126be266c0715815198.png) που μπορούν να γραφτούν σε αυτή τη μορφή. Αν χρησιμοποιήσουμε μόνο τους αριθμούς
που μπορούν να γραφτούν σε αυτή τη μορφή. Αν χρησιμοποιήσουμε μόνο τους αριθμούς  , μπορούμε να πάρουμε το πολύ
, μπορούμε να πάρουμε το πολύ  αριθμούς. Αυτοί θα είναι στο διάστημα
αριθμούς. Αυτοί θα είναι στο διάστημα ![[0,2^{k+1}+k] [0,2^{k+1}+k]](/forum/ext/geomar/texintegr/latexrender/pictures/02262eb2d9c1d8c00b514f9530856642.png) . Από αυτούς, τουλάχιστον
. Από αυτούς, τουλάχιστον  θα είναι στο διάστημα
θα είναι στο διάστημα ![[2^{k+1}+1,2^{k+1}+k] [2^{k+1}+1,2^{k+1}+k]](/forum/ext/geomar/texintegr/latexrender/pictures/3e9f51324b1b6468b1493d9a2c6d90d9.png) . (Επειδή
. (Επειδή  , τότε μπορώ να γράψω τον
, τότε μπορώ να γράψω τον  αν και μόνο αν μπορώ να γράψω και τον
αν και μόνο αν μπορώ να γράψω και τον  .) Επομένως παίρνω
.) Επομένως παίρνω  . Αν τώρα γράψω
. Αν τώρα γράψω  το πλήθος των ακεραίων στο διάστημα
το πλήθος των ακεραίων στο διάστημα  . Επειδή προφανώς
. Επειδή προφανώς  , τότε έχω
, τότε έχω  . Δηλαδή για κάθε
. Δηλαδή για κάθε 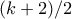 μη αρνητικούς ακεραίους που δεν μπορούν να γραφτούν στη ζητούμενη μορφή.
μη αρνητικούς ακεραίους που δεν μπορούν να γραφτούν στη ζητούμενη μορφή.