4. Για τα δυο ενδεχόμενα
 για τα οποία ισχύει
για τα οποία ισχύει
Ποιά η τιμή του
 ;
;6. Θεωρώντας ότι
 είναι η μέση τιμή τυχαίου δείγματος μεγέθους
είναι η μέση τιμή τυχαίου δείγματος μεγέθους 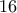 από πληθυσμό που ακολουθεί την κανονική κατανομή
από πληθυσμό που ακολουθεί την κανονική κατανομή  , ποιά η τιμή του
, ποιά η τιμή του  ;
;8. Πόσο ισούται το εμβαδόν που περικλείεται από την καμπύλη
 , των άξονα των
, των άξονα των  και τις δυο ευθείες
και τις δυο ευθείες  ,
,  ;
;9. Δίνονται
 κάρτες με τα γράμματα
κάρτες με τα γράμματα  και
και  και
και  κάρτες με τα ψηφία
κάρτες με τα ψηφία  και
και  γραμμένα σε αυτές. Αν και οι
γραμμένα σε αυτές. Αν και οι  κάρτες, από μια φορά η κάθε μία, τοποθετηθούν στην σειρά κατά τυχαίο τρόπο, ποιά η πιθανότητα κάρτα με ψηφίο να τοποθετηθεί δίπλα στην κάρτα με το γράμμα
κάρτες, από μια φορά η κάθε μία, τοποθετηθούν στην σειρά κατά τυχαίο τρόπο, ποιά η πιθανότητα κάρτα με ψηφίο να τοποθετηθεί δίπλα στην κάρτα με το γράμμα  ;
;10. Δίνεται τρίγωνο
 με
με  και
και  . Ποιό είναι το μήκος της πλευράς
. Ποιό είναι το μήκος της πλευράς  αν η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου
αν η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου  είναι ίση με
είναι ίση με  ;
;11. Ποιά η τιμή του
 ;
;14. Έστω
 ορθογώνιο με
ορθογώνιο με  και
και  όπως στο σχήμα. Έστω
όπως στο σχήμα. Έστω  σημείο του
σημείο του  που το διαιρεί σε λόγο
που το διαιρεί σε λόγο  και
και 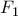 εσωτερικό σημείο του
εσωτερικό σημείο του  για το οποίο
για το οποίο  και
και  . Σχεδιάζουμε το τρίγωνο
. Σχεδιάζουμε το τρίγωνο  , σκιαγραφούμε το τετράπλευρο
, σκιαγραφούμε το τετράπλευρο  και έστω
και έστω 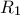 το σχήμα που προκύπτει.
το σχήμα που προκύπτει. Στο σχήμα
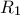 σχεδιάζουμε το ορθογώνιο
σχεδιάζουμε το ορθογώνιο  ,
,  με κορυφές το σημείο
με κορυφές το σημείο 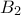 στο τμήμα
στο τμήμα  , το σημείο
, το σημείο 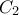 στο τμήμα
στο τμήμα  , το σημείο
, το σημείο  στο τμήμα
στο τμήμα  και το σημείο
και το σημείο  . Έστω
. Έστω  το σχήμα που προκύπτει σχεδιάζοντας το τρίγωνο
το σχήμα που προκύπτει σχεδιάζοντας το τρίγωνο  στο ορθογώνιο
στο ορθογώνιο  και σκιαγράφοντας το τετράπλευρο
και σκιαγράφοντας το τετράπλευρο  όπως στο σχήμα
όπως στο σχήμα 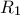 .
.Συνεχίζοντας την διαδικασία, ας είναι
 το εμβαδόν του σκιαγραφημένου τμήματος του σχήματος
το εμβαδόν του σκιαγραφημένου τμήματος του σχήματος  . Ποιά είναι η τιμή του
. Ποιά είναι η τιμή του  ;
;18. Για τον πραγματικό αριθμό
 έστω η συνάρτηση
έστω η συνάρτηση  με
με 
Ποιό είναι το άθροισμα των τιμών του
 για τις οποίες
για τις οποίες 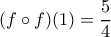 ;
;20. Δίνεται η συνάρτηση
 και έστω
και έστω  συνάρτηση με πεδίο ορισμού το σύνολο των πραγματικών αριθμών και σύνολο τιμών το σύνολο
συνάρτηση με πεδίο ορισμού το σύνολο των πραγματικών αριθμών και σύνολο τιμών το σύνολο  . Αν ο φυσικός αριθμός
. Αν ο φυσικός αριθμός  ικανοποιεί τις παρακάτω συνθήκες, ποιά η τιμή του;
ικανοποιεί τις παρακάτω συνθήκες, ποιά η τιμή του;Η συνάρτηση
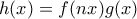 είναι συνεχής στο σύνολο των πραγματικών αριθμών και
είναι συνεχής στο σύνολο των πραγματικών αριθμών και 
21. Δίνεται η ακολουθία
 με
με  και για όλους τους φυσικούς αριθμούς
και για όλους τους φυσικούς αριθμούς  ικανοποιεί τις συνθήκες:
ικανοποιεί τις συνθήκες:α)

β)

αν
 , ποιά η τιμή του
, ποιά η τιμή του  ;
;22. Στην ανάπτυξη του
 , να βρείτε τον συντελεστή του
, να βρείτε τον συντελεστή του  .
.27. Να βρείτε το πλήθος των φυσικών αριθμών
 , ώστε η παράσταση
, ώστε η παράσταση 
ναι είναι μικρότερη ή ίση του
 .
.28. Έστω
 συνάρτηση που δίνεται από τον τύπο
συνάρτηση που δίνεται από τον τύπο  , όπου
, όπου  σταθερές. Έστω
σταθερές. Έστω  η αντίστροφη συνάρτηση της
η αντίστροφη συνάρτηση της  . Να βρείτε την τιμή
. Να βρείτε την τιμή  , αν η σύνθετη συνάρτηση
, αν η σύνθετη συνάρτηση  ικανοποιεί τις συνθήκες:
ικανοποιεί τις συνθήκες:α) η συνάρτηση
 είναι παραγωγίσιμη για όλους τους πραγματικούς αριθμούς
είναι παραγωγίσιμη για όλους τους πραγματικούς αριθμούςβ)
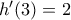
30. Η συνάρτηση
 με πεδίο ορισμού το σύνολο των πραγματικών αριθμών, όπου
με πεδίο ορισμού το σύνολο των πραγματικών αριθμών, όπου  κυβικό πολυώνυμο με μεγιστοβάθμιο συντελεστή ίσο με
κυβικό πολυώνυμο με μεγιστοβάθμιο συντελεστή ίσο με  , ικανοποιεί τις ακόλουθες συνθήκες
, ικανοποιεί τις ακόλουθες συνθήκεςα) Για
 το πλήθος των
το πλήθος των  στα οποία η
στα οποία η  μεγιστοποιείται (τοπικά μέγιστα) είναι ίσο με
μεγιστοποιείται (τοπικά μέγιστα) είναι ίσο με  και όλες οι τιμές της στα τοπικά μέγιστα είναι ίσες.
και όλες οι τιμές της στα τοπικά μέγιστα είναι ίσες. β) Η μέγιστη τιμή της
 είναι ίση με
είναι ίση με  και η ελάχιστη
και η ελάχιστη  .
.Να βρείτε την τιμή της παράστασης
 , αν
, αν 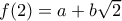 (όπου
(όπου  ρητοί αριθμοί).
ρητοί αριθμοί).
 , δηλαδή
, δηλαδή  .
. στην θέση του
στην θέση του  είναι παντού παραγωγίσιμη. Οπότε από την
είναι παντού παραγωγίσιμη. Οπότε από την  έχουμε ότι η
έχουμε ότι η  είναι παντού παραγωγίσιμη. Διαιρώντας με το
είναι παντού παραγωγίσιμη. Διαιρώντας με το  , συμβαίνει το ίδιο με την
, συμβαίνει το ίδιο με την  .
.  του ορίου
του ορίου 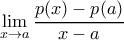 (που εξ υποθέσεως υπάρχουν και είναι ίσα), έπεται
(που εξ υποθέσεως υπάρχουν και είναι ίσα), έπεται  και άρα
και άρα  . H
. H 
 . Για
. Για  έπεται
έπεται 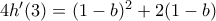 που με χρήση της β) δίνει
που με χρήση της β) δίνει 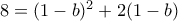 . Λύνοντας την δευτεροβάθμια είναι
. Λύνοντας την δευτεροβάθμια είναι  ή
ή 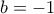 αλλά κρατάμε την πρώτη αφού
αλλά κρατάμε την πρώτη αφού  .
. , και λοιπά.
, και λοιπά.

 .
.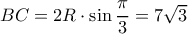


 .
.

 και έτσι
και έτσι 
 μας δίνει
μας δίνει  και έτσι
και έτσι 
 βρίσκεται πλέον εύκολα
βρίσκεται πλέον εύκολα 