Πρέπει

.
Αναγκαίο: Έστω χωρίς βλάβη της γενικότητας ότι

. Από την τριγωνική ανισότητα είναι

Ικανό: Θα το δείξω αρχικά με την επιπλέον προϋπόθεση ότι

. Θα προχωρήσω με επαγωγή στο

. Η περίπτωση

είναι άμεση αφού η συνθήκη

δίνει

.
Θέτω

. Υπάρχει (πιθανώς εκφυλισμένο) τρίγωνο με μήκη πλευρών
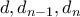
αφού:



Μπορώ λοιπόν να πάρω σημεία

ώστε

και

.
Ισχύει όμως ότι

(άμεσο) και

αφού

Από την επαγωγική υπόθεση λοιπόν μπορώ να κλείσω το πολύγωνο.
Μένει τώρα να απαλλαχθώ από την επιπλέον προϋπόθεση ότι

. Έχω όμως

διανύσματα με μήκη

τα οποία όταν τα τοποθετήσω διαδοχικά δημιουργούν ένα πολύγωνο. Δηλαδή έχουν άθροισμα

. Όμως με οποιαδήποτε σειρά και να τα τοποθετήσω πάλι θα δημιουργούν πολύγωνο. Οπότε ο ισχυρισμός αποδείχθηκε.
Η πρώτη λύση που έδωσα ήταν όπως παρατήρησε ο Δημήτρης σε π.μ. λανθασμένη. Ελπίζω τώρα να είμαι σωστός.
 θετικοί πραγματικοί αριθμοί με
θετικοί πραγματικοί αριθμοί με  . Να βρεθεί αναγκαία και ικανή συνθήκη επί των
. Να βρεθεί αναγκαία και ικανή συνθήκη επί των  για να υπάρχει ακολουθία σημείων του Ευκλείδειου επιπέδου
για να υπάρχει ακολουθία σημείων του Ευκλείδειου επιπέδου  έτσι ώστε:
έτσι ώστε:  η απόσταση μεταξύ των
η απόσταση μεταξύ των  και
και  να είναι
να είναι  και
και
 :
:
 .
. . Από την τριγωνική ανισότητα είναι
. Από την τριγωνική ανισότητα είναι 
 . Θα προχωρήσω με επαγωγή στο
. Θα προχωρήσω με επαγωγή στο  . Η περίπτωση
. Η περίπτωση  είναι άμεση αφού η συνθήκη
είναι άμεση αφού η συνθήκη  δίνει
δίνει  .
.  . Υπάρχει (πιθανώς εκφυλισμένο) τρίγωνο με μήκη πλευρών
. Υπάρχει (πιθανώς εκφυλισμένο) τρίγωνο με μήκη πλευρών 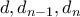 αφού:
αφού:


 ώστε
ώστε  και
και  .
. (άμεσο) και
(άμεσο) και  αφού
αφού
 τα οποία όταν τα τοποθετήσω διαδοχικά δημιουργούν ένα πολύγωνο. Δηλαδή έχουν άθροισμα
τα οποία όταν τα τοποθετήσω διαδοχικά δημιουργούν ένα πολύγωνο. Δηλαδή έχουν άθροισμα  . Όμως με οποιαδήποτε σειρά και να τα τοποθετήσω πάλι θα δημιουργούν πολύγωνο. Οπότε ο ισχυρισμός αποδείχθηκε.
. Όμως με οποιαδήποτε σειρά και να τα τοποθετήσω πάλι θα δημιουργούν πολύγωνο. Οπότε ο ισχυρισμός αποδείχθηκε. ,
,  και στη συνέχεια "ένωσα" τα
και στη συνέχεια "ένωσα" τα  σε
σε  . Αν
. Αν  η επαγωγική υπόθεση χρησιμοποιείται επί τόπου. Αλλιώς παρατηρούμε ότι
η επαγωγική υπόθεση χρησιμοποιείται επί τόπου. Αλλιώς παρατηρούμε ότι  (ισχύει
(ισχύει  ) και χρησιμοποιούμε την επαγωγική υπόθεση με το
) και χρησιμοποιούμε την επαγωγική υπόθεση με το  ως μέγιστο.
ως μέγιστο.