dement έγραψε:Αλέξανδρε (;), έχω την εντύπωση ότι το λήμμα της αντανάκλασης τώρα δεν προσφέρεται τόσο για την περίπτωσή μας. Δύο μονοπάτια που αντιστοιχίζονται από το λήμμα
ταυτίζονται μέχρι το ποτάμι και στη συνέχεια
ο βορράς γίνεται ανατολή και τούμπαλιν, μέχρι το επόμενο πέρασμα και πάει λέγοντας. Η ασυμμετρία που εισάγεται από τις διαφορετικές τιμές των
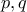
χαλάει τη δουλειά...
Α, και η κοπέλα λέγεται Αλέσσια.


Αλέσσια ωραίο όνομα, δε θα έπρεπε να κάνω λάθος, στο πρόβλημα συγχωρείται

.
Μια δεύτερη σκέψη που χρονικά ήταν η πρώτη που έκανα είναι να θεωρήσουμε το συμπληρωματικό ενδεχόμενο

και να δείξουμε ότι

(1).
Το

είναι το ενδεχόμενο σε

κινήσεις να μην διέσχισε το ποτάμι ούτε μια φορά. Παρατηρούμε ότι για τα σημεία πάνω από την

θα πρέπει να αναγκαστηκά να το διασχίσει οπότε το ενδεχόμενο αυτό θα αποτελείτε από τις διαδρομές στα σημεία της ευθείας

που βρίσκονται κάτω από την ευθεία

και δεν διασχίζουν το ποτάμι.
Από το πρώτο ερώτημα για κάθε τέτοιο σημείο οι δυνατοί τρόποι για το προσεγγίσουμε είναι

(2) . Τα σημεία προς εξέταση είναι τα

όπου

.
Εφαρμόζοντας την (2) για τα παραπάνω σημεία αντίστοιχα βρίσκουμε
![[ \binom{n}{n} -\binom{n}{n+1} ] [ \binom{n}{n} -\binom{n}{n+1} ]](/forum/ext/geomar/texintegr/latexrender/pictures/ed048e1e03e6950d8a580074704c6301.png)
τρόποι με πιθανότητα

γιατί κινούμαστε

κινήσεις ανατολικά και 0 κινήσεις βόρεια. Ομοίως για τα άλλα σημεία
![[ \binom{n}{n-1} -\binom{n}{n} ] p^{n-1}q^{1} [ \binom{n}{n-1} -\binom{n}{n} ] p^{n-1}q^{1}](/forum/ext/geomar/texintegr/latexrender/pictures/5602e0afe4b53a4e2d754feeb2f20439.png)
![[ \binom{n}{n-2} -\binom{n}{n-1} ] p^{n-2}q^{2} [ \binom{n}{n-2} -\binom{n}{n-1} ] p^{n-2}q^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/690f6e8188abaaaff39b6e843264f275.png)
....
![[ \binom{n}{n-k} -\binom{n}{n-k-1} ] p^{n-k-1}q^{k} [ \binom{n}{n-k} -\binom{n}{n-k-1} ] p^{n-k-1}q^{k}](/forum/ext/geomar/texintegr/latexrender/pictures/44c122199c324ba021e1cc8e61f73cf1.png)
Πολλαπλασιάζοντας και διαιρώντας τους όρους με το (-) με

και αθροίζοντας τις παραπάνω πιθανότητες βρίσκουμε
![\sum_{i=n-k}^{n} \binom{n}{i} p^{i}q^{n-i} - \dfrac{q}{p} [ \sum_{i=n-k-1}^{n} \binom{n}{i} p^{i}q^{n-i} ] \sum_{i=n-k}^{n} \binom{n}{i} p^{i}q^{n-i} - \dfrac{q}{p} [ \sum_{i=n-k-1}^{n} \binom{n}{i} p^{i}q^{n-i} ]](/forum/ext/geomar/texintegr/latexrender/pictures/11e78efc33e551c0c655e3382832c306.png)
(3)
Αν

η αθροιστική συνάρτηση κατανομής της διωνυμικής κατανομής τότε η (1) με την βοήθεια της (3) μπορεί να γραφεί


εδώ προς το παρόν και πάλι έχω κολλήσει...πάλι κάποιες σκέψεις είναι είτε επαγωγικά, είτε αξιοποιώντας ίσως την μονοτόνία της

...
Ελπίζω να είναι σωστά τώρα τουλάχιστον.
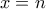 και
και  , όπου
, όπου  τυχαίος ακέραιος. Έτσι, οι διασταυρώσεις της είναι ακριβώς τα σημεία με ακέραιες συντεταγμένες. Επιπλέον, η πόλη διασχίζεται από τον ποταμό Orna ο οποίος αντιστοιχεί στην ευθεία
τυχαίος ακέραιος. Έτσι, οι διασταυρώσεις της είναι ακριβώς τα σημεία με ακέραιες συντεταγμένες. Επιπλέον, η πόλη διασχίζεται από τον ποταμό Orna ο οποίος αντιστοιχεί στην ευθεία  (βλ. σχήμα).
(βλ. σχήμα). και κινείται πάντα είτε βόρεια είτε ανατολικά.
και κινείται πάντα είτε βόρεια είτε ανατολικά. χωρίς να διασχίσει το ποτάμι.
χωρίς να διασχίσει το ποτάμι. και βόρεια με πιθανότητα
και βόρεια με πιθανότητα  . Να αποδειχθεί ότι η πιθανότητα να διασχίσει τουλάχιστον μία φορά το ποτάμι σε μία διαδρομή με
. Να αποδειχθεί ότι η πιθανότητα να διασχίσει τουλάχιστον μία φορά το ποτάμι σε μία διαδρομή με  διασταυρώσεις είναι μικρότερη ή ίση με
διασταυρώσεις είναι μικρότερη ή ίση με  .
.
 κινήσεις ανατολικά και
κινήσεις ανατολικά και  κινήσεις βόρεια. Οπότε το πλήθος τέτοιων διαδρομών ισούται με τον αριθμό των τρόπων να διαλέξουμε από
κινήσεις βόρεια. Οπότε το πλήθος τέτοιων διαδρομών ισούται με τον αριθμό των τρόπων να διαλέξουμε από  αριθμό κινήσεων,
αριθμό κινήσεων, 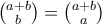 τρόποι.
τρόποι. ) που υπερβαίνουν την ευθεία
) που υπερβαίνουν την ευθεία  ισούται με το πλήθος των διαδρομών από το σημείο
ισούται με το πλήθος των διαδρομών από το σημείο  .
. 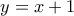 . Εξετάζουμε το πρώτο σημείο τομής με αυτή την ευθεία και πάιρνουμε την συμμετρική διαδρομή από αυτό το σημείο και ύστερα μέχρι το
. Εξετάζουμε το πρώτο σημείο τομής με αυτή την ευθεία και πάιρνουμε την συμμετρική διαδρομή από αυτό το σημείο και ύστερα μέχρι το  σημαίνει ότι το διασχίζουμε όταν υπερβαίνουμε την ευθεία
σημαίνει ότι το διασχίζουμε όταν υπερβαίνουμε την ευθεία 
 ο παραπάνω τύπος δίνει τους αριθμούς Catalan.
ο παραπάνω τύπος δίνει τους αριθμούς Catalan.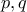 χαλάει τη δουλειά...
χαλάει τη δουλειά... και να δείξουμε ότι
και να δείξουμε ότι  (1).
(1). που βρίσκονται κάτω από την ευθεία
που βρίσκονται κάτω από την ευθεία  και δεν διασχίζουν το ποτάμι.
και δεν διασχίζουν το ποτάμι.  (2) . Τα σημεία προς εξέταση είναι τα
(2) . Τα σημεία προς εξέταση είναι τα 
 .
.![[ \binom{n}{n} -\binom{n}{n+1} ] [ \binom{n}{n} -\binom{n}{n+1} ]](/forum/ext/geomar/texintegr/latexrender/pictures/ed048e1e03e6950d8a580074704c6301.png) τρόποι με πιθανότητα
τρόποι με πιθανότητα  γιατί κινούμαστε
γιατί κινούμαστε ![[ \binom{n}{n-1} -\binom{n}{n} ] p^{n-1}q^{1} [ \binom{n}{n-1} -\binom{n}{n} ] p^{n-1}q^{1}](/forum/ext/geomar/texintegr/latexrender/pictures/5602e0afe4b53a4e2d754feeb2f20439.png)
![[ \binom{n}{n-2} -\binom{n}{n-1} ] p^{n-2}q^{2} [ \binom{n}{n-2} -\binom{n}{n-1} ] p^{n-2}q^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/690f6e8188abaaaff39b6e843264f275.png)
![[ \binom{n}{n-k} -\binom{n}{n-k-1} ] p^{n-k-1}q^{k} [ \binom{n}{n-k} -\binom{n}{n-k-1} ] p^{n-k-1}q^{k}](/forum/ext/geomar/texintegr/latexrender/pictures/44c122199c324ba021e1cc8e61f73cf1.png)
 και αθροίζοντας τις παραπάνω πιθανότητες βρίσκουμε
και αθροίζοντας τις παραπάνω πιθανότητες βρίσκουμε![\sum_{i=n-k}^{n} \binom{n}{i} p^{i}q^{n-i} - \dfrac{q}{p} [ \sum_{i=n-k-1}^{n} \binom{n}{i} p^{i}q^{n-i} ] \sum_{i=n-k}^{n} \binom{n}{i} p^{i}q^{n-i} - \dfrac{q}{p} [ \sum_{i=n-k-1}^{n} \binom{n}{i} p^{i}q^{n-i} ]](/forum/ext/geomar/texintegr/latexrender/pictures/11e78efc33e551c0c655e3382832c306.png) (3)
(3) η αθροιστική συνάρτηση κατανομής της διωνυμικής κατανομής τότε η (1) με την βοήθεια της (3) μπορεί να γραφεί
η αθροιστική συνάρτηση κατανομής της διωνυμικής κατανομής τότε η (1) με την βοήθεια της (3) μπορεί να γραφεί 

 η ζητούμενη πιθανότητα. Τότε
η ζητούμενη πιθανότητα. Τότε  , όπου
, όπου 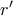 είναι η πιθανότητα να διασχίσουμε το ποτάμι ξεκινώντας από το
είναι η πιθανότητα να διασχίσουμε το ποτάμι ξεκινώντας από το  και κάνοντας
και κάνοντας  κινήσεις. Για να το επιτύχουμε όμως αυτό πρέπει πρώτα να διασχίσουμε το υποθετικό ποτάμι με εξίσωση
κινήσεις. Για να το επιτύχουμε όμως αυτό πρέπει πρώτα να διασχίσουμε το υποθετικό ποτάμι με εξίσωση  , και μετά ο πραγματικό ποτάμι με εξίσωση
, και μετά ο πραγματικό ποτάμι με εξίσωση  . Από συμμετρία, η πιθανότητα να διασχίσουμε το υποθετικό ποτάμι είναι το πολύ
. Από συμμετρία, η πιθανότητα να διασχίσουμε το υποθετικό ποτάμι είναι το πολύ  . Τότε πρέπει να διασχίσουμε το κανονικό ποτάμι σε
. Τότε πρέπει να διασχίσουμε το κανονικό ποτάμι σε 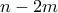 κινήσεις και η πιθανότητα να το πετύχουμε αυτό είναι πάλι το πολύ
κινήσεις και η πιθανότητα να το πετύχουμε αυτό είναι πάλι το πολύ 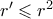 . Άρα
. Άρα 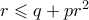 ή ισοδύναμα
ή ισοδύναμα  . Όμως
. Όμως  αφού με πιθανότητα
αφού με πιθανότητα  κινούμαστε πάντα ανατολικά. Άρα πρέπει
κινούμαστε πάντα ανατολικά. Άρα πρέπει  .
. αν
αν  και ισούται με
και ισούται με  αν
αν  .
. , όπου
, όπου  ο αντίστοιχος αριθμός Catalan. Αθροίζοντας για όλα τα
ο αντίστοιχος αριθμός Catalan. Αθροίζοντας για όλα τα  παίρνουμε τη γεννήτρια συνάρτηση της ακολουθίας Catalan για
παίρνουμε τη γεννήτρια συνάρτηση της ακολουθίας Catalan για  και το άπειρο άθροισμα ισούται με
και το άπειρο άθροισμα ισούται με
 . Μας ενδιαφέρει αν θα καταφέρουμε σε
. Μας ενδιαφέρει αν θα καταφέρουμε σε  .
. για την πιθανότητα, αν ξεκινήσω από τον φυσικό
για την πιθανότητα, αν ξεκινήσω από τον φυσικό  . Επίσης είναι
. Επίσης είναι 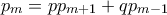 . Η χαρακτηριστική εξίσωση είναι η
. Η χαρακτηριστική εξίσωση είναι η  που έχει ρίζες τα
που έχει ρίζες τα  και
και  .
. για κάποιες σταθερές
για κάποιες σταθερές  . Η περίπτωση
. Η περίπτωση  δίνει
δίνει  . Καταλήγουμε λοιπόν στην
. Καταλήγουμε λοιπόν στην  .
. τα πράγματα είναι απλά αφού έχουμε
τα πράγματα είναι απλά αφού έχουμε  για κάθε
για κάθε 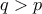 τα πράγματα είναι εύκολα παίρνοντας το όριο όταν το
τα πράγματα είναι εύκολα παίρνοντας το όριο όταν το  , άρα
, άρα  και άρα πάλι
και άρα πάλι  πέραν του ότι
πέραν του ότι  το οποίο προκύπτει αν πάρουμε το όριο στο άπειρο.
το οποίο προκύπτει αν πάρουμε το όριο στο άπειρο.  για κάθε
για κάθε