dement έγραψε:1. Μία συσκευή μνήμης υπολογιστή έχει τη μορφή ορθογωνίου παραλληλογράμμου ακέραιων διαστάσεων

χωρισμένου σε κελιά
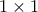
έτσι ώστε σε κάθε κελί να αποθηκεύεται ένα bit (δυαδικό ψηφίο,

ή

). Για τεχνικούς λόγους το άθροισμα κάθε σειράς και κάθε στήλης πρέπει να είναι περιττό. Πόσες διαφορετικές διατάξεις μπορούν να αποθηκευτούν;
Θα δείξουμε ότι όταν τα

και

είναι το ένα είναι άρτιο και το άλλο περιττό τότε δεν υπάρχει καμία διάταξη, ενώ όταν είναι
και τα δύο άρτια ή και τα δύο περιττά τότε θα έχουμε

διατάξεις.
1) Αν τα  και
και  είναι το ένα είναι άρτιο και το άλλο περιττό.
είναι το ένα είναι άρτιο και το άλλο περιττό.
Φαίνεται εύκολα σε πίνακα

ότι δεν υπάρχει σωστή διάταξη αλλά θα το γενικεύσουμε.

Έστω ότι το

είναι άρτιος αριθμός και το

είναι περιττός. Ας υποθέσουμε ότι είναι εφικτή μια διάταξη με περιττό άθροισμα ανά γραμμή και ανά στήλη. Αν

το άθροισμα των αθροισμάτων ανά γραμμή τότε, επειδή προκύπτει από άρτιο πλήθος περιττών προσθετέων, θα είναι άρτιος αριθμός. Αν

το άθροισμα των αθροισμάτων ανά στήλη τότε, επειδή προκύπτει από περιττό πλήθος περιττών προσθετέων, θα είναι περιττός αριθμός. Όμως επειδή πρέπει

καταλήγουμε σε άτοπο. Το ίδιο γίνεται και όταν το

είναι περιττός και το

άρτιος.
2) Αν τα  και
και  είναι και τα δύο άρτια ή και τα δύο περιττά.
είναι και τα δύο άρτια ή και τα δύο περιττά.
Γεμίζουμε όλο τον πίνακα στην τύχη με

και

, εκτός από την τελευταία γραμμή και την τελευταία στήλη. Θα έχουμε

διαφορετικές διατάξεις.
Η συμπλήρωση του τελευταίου κελιού κάθε μιας από τις

πρώτες γραμμές γίνεται με μοναδικό τρόπο. Έτσι αν η γραμμή έχει ήδη περιττό αριθμό από

τότε βάζουμε

αλλιώς βάζουμε

.
Το ίδιο γίνεται για το τελευταίο κελί κάθε μιας από τις

πρώτες στήλες.
Στο τελευταίο κελί της τελευταίας γραμμής, που ταυτίζεται με το τελευταίο κελί της τελευταίας στήλης, θα βάλουμε με μοναδικό τρόπο

ή

ώστε η τελευταία γραμμή να έχει περιττό αριθμό από

και θα δείξουμε παρακάτω ότι έτσι θα έχει περιττό αριθμό από

και η τελευταία στήλη.
Έτσι θα έχουμε τελικά

διαφορετικές διατάξεις.
Για να κλείσουμε την εκκρεμότητα με το τελευταίο κελί ας δούμε μια διαφορετική διαδικασία.
Έστω

μία από τις

διαφορετικές διατάξεις, η οποία θα έχει

ψηφία ίσα με

στα πρώτα

κελιά.
Ακολουθούμε τα εξής βήματα:
Ξεκινάμε με έναν πίνακα

που θα έχει παντού

εκτός από την τελευταία γραμμή και την τελευταία στήλη που θα έχει παντού

. Ειδικά το τελευταίο κελί θα έχει

αν τα

και

είναι και τα δύο άρτια, ενώ θα έχει

αν τα

και

είναι και τα δύο περιττά. Π.χ.

ή

Με αυτόν τον τρόπο ο πίνακας θα έχει ήδη περιττά αθροίσματα ανά γραμμή και ανά στήλη.
Για κάθε ένα ψηφίο

από τα

της διάταξης

αντικαθιστούμε στην αντίστοιχη θέση του πίνακα

το

με

. Ταυτόχρονα θα αλλάζει (από

σε

, ή από

σε

αν έχει ήδη αλλάξει από προηγούμενο βήμα) το τελευταίο κελί της αντίστοιχης γραμμής αλλά και της αντίστοιχης στήλης ώστε τα αθροίσματά τους να παραμένουν περιττά. Και ταυτόχρονα θα αλλάζει το τελευταίο κελί του πίνακα. Επομένως σε κάθε βήμα όλες οι γραμμές και όλες οι στήλες θα συνεχίζουν να έχουν περιττά αθροίσματα.
Μάλιστα, αν το

είναι άρτιο τότε το τελευταίο κελί του πίνακα θα έχει το ίδιο ψηφίο με το οποίο ξεκίνησε η διαδικασία, ενώ αν το

είναι περιττό το τελευταίο κελί θα έχει αλλάξει.
Υ.Γ. Δεν είμαι σίγουρος αν για το τελευταίο κελί τα παραπάνω αποτελούν επαρκή απόδειξη. Δεν μπόρεσα να βρω κάτι πιο σύντομο και κατανοητό.
Προφανώς χωρίς
αυτήν δεν θα μπορούσα να βρω καμία λύση.
 χωρισμένου σε κελιά
χωρισμένου σε κελιά 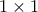 έτσι ώστε σε κάθε κελί να αποθηκεύεται ένα bit (δυαδικό ψηφίο,
έτσι ώστε σε κάθε κελί να αποθηκεύεται ένα bit (δυαδικό ψηφίο,  ή
ή  ). Για τεχνικούς λόγους το άθροισμα κάθε σειράς και κάθε στήλης πρέπει να είναι περιττό. Πόσες διαφορετικές διατάξεις μπορούν να αποθηκευτούν;
). Για τεχνικούς λόγους το άθροισμα κάθε σειράς και κάθε στήλης πρέπει να είναι περιττό. Πόσες διαφορετικές διατάξεις μπορούν να αποθηκευτούν; χωρισμένο σε κελιά
χωρισμένο σε κελιά  στα οποία αποθηκεύεται ένα bit. Και πάλι το άθροισμα των περιεχομένων των κελιών κατά μήκος μιας διάστασης (κρατώντας τις άλλες δύο σταθερές) πρέπει να είναι περιττό. Πόσες διαφορετικές διατάξεις μπορούν να αποθηκευτούν;
στα οποία αποθηκεύεται ένα bit. Και πάλι το άθροισμα των περιεχομένων των κελιών κατά μήκος μιας διάστασης (κρατώντας τις άλλες δύο σταθερές) πρέπει να είναι περιττό. Πόσες διαφορετικές διατάξεις μπορούν να αποθηκευτούν;
 και
και  είναι το ένα είναι άρτιο και το άλλο περιττό τότε δεν υπάρχει καμία διάταξη, ενώ όταν είναι
είναι το ένα είναι άρτιο και το άλλο περιττό τότε δεν υπάρχει καμία διάταξη, ενώ όταν είναι  διατάξεις.
διατάξεις. ότι δεν υπάρχει σωστή διάταξη αλλά θα το γενικεύσουμε.
ότι δεν υπάρχει σωστή διάταξη αλλά θα το γενικεύσουμε.
 το άθροισμα των αθροισμάτων ανά γραμμή τότε, επειδή προκύπτει από άρτιο πλήθος περιττών προσθετέων, θα είναι άρτιος αριθμός. Αν
το άθροισμα των αθροισμάτων ανά γραμμή τότε, επειδή προκύπτει από άρτιο πλήθος περιττών προσθετέων, θα είναι άρτιος αριθμός. Αν  το άθροισμα των αθροισμάτων ανά στήλη τότε, επειδή προκύπτει από περιττό πλήθος περιττών προσθετέων, θα είναι περιττός αριθμός. Όμως επειδή πρέπει
το άθροισμα των αθροισμάτων ανά στήλη τότε, επειδή προκύπτει από περιττό πλήθος περιττών προσθετέων, θα είναι περιττός αριθμός. Όμως επειδή πρέπει  καταλήγουμε σε άτοπο. Το ίδιο γίνεται και όταν το
καταλήγουμε σε άτοπο. Το ίδιο γίνεται και όταν το  διαφορετικές διατάξεις.
διαφορετικές διατάξεις. πρώτες γραμμές γίνεται με μοναδικό τρόπο. Έτσι αν η γραμμή έχει ήδη περιττό αριθμό από
πρώτες γραμμές γίνεται με μοναδικό τρόπο. Έτσι αν η γραμμή έχει ήδη περιττό αριθμό από  πρώτες στήλες.
πρώτες στήλες. διαφορετικές διατάξεις.
διαφορετικές διατάξεις. μία από τις
μία από τις  ψηφία ίσα με
ψηφία ίσα με  κελιά.
κελιά. που θα έχει παντού
που θα έχει παντού 

 είναι όλα άρτια ή όλα περιττά τότε θα έχουμε
είναι όλα άρτια ή όλα περιττά τότε θα έχουμε  διατάξεις, ενώ σε κάθε άλλη περίπτωση δεν θα έχουμε καμία.
διατάξεις, ενώ σε κάθε άλλη περίπτωση δεν θα έχουμε καμία.