1. α) Να διαπιστώσετε οτι όποιοι και αν είναι οι πραγματικοί αριθμοί
 και
και  , έχει μηδενική τιμή η έκφραση
, έχει μηδενική τιμή η έκφραση 
β) Να διαπιστώσετε οτι οποιοσδήποτε και αν είναι ο πραγματικός αριθμός
 , έχει τιμή μονάδα η έκφραση
, έχει τιμή μονάδα η έκφραση
2. Να βρεθούν δυο διάφοροι του μηδενός αριθμοί των οποίων το άθροισμα, το γινόμενο και το πηλίκο είναι ίσα.
3. Ακέραιο ως προς
 πολυώνυμο, διαιρούμενο από το
πολυώνυμο, διαιρούμενο από το  δίνει ως υπόλοιπο την έκφραση
δίνει ως υπόλοιπο την έκφραση  .
. Ποια είναι τα υπόλοιπα που προκύπτουν, αν το πολυώνυμο διαιρεθεί με τα διώνυμα
α)

β)
 ;
;edit's
διόρθωση (λόγω latex) τυπογραφικό στο 3ο
διόρθωση στο 1β, ευχαριστώ τον Γιώργο (Βισβίκη) που το πρόσεξε

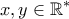 οι αριθμοί. Τότε ισχύουν
οι αριθμοί. Τότε ισχύουν  .
. .
. Αν
Αν  η (2) γίνεται
η (2) γίνεται  και είναι αδύνατη
και είναι αδύνατη η (2) γίνεται
η (2) γίνεται  .
.
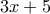 .
.  το πολυώνυμο, η ταυτότητα της διαίρεσης γράφεται :
το πολυώνυμο, η ταυτότητα της διαίρεσης γράφεται : 
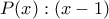 είναι ίσο με
είναι ίσο με 
 είναι ίσο με
είναι ίσο με 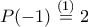
 γράφεται:
γράφεται:

 ...",
...", 

 , για κάθε
, για κάθε  .
. μηδενίζεται για
μηδενίζεται για 
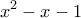 που μηδενίζεται για
που μηδενίζεται για 