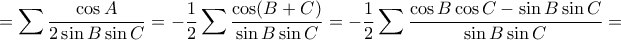1. Να αποδειχθεί οτι σε κάθε τρίγωνο
 αληθεύει η σχέση:
αληθεύει η σχέση: .
.2. Να επιλυθεί τρίγωνο
 στο οποίο γνωρίζουμε την πλευρά
στο οποίο γνωρίζουμε την πλευρά  , την διάμεσο
, την διάμεσο  και την αλγεβρική τιμή
και την αλγεβρική τιμή  , όπου
, όπου  είναι το ίχνος του ύψους που άγεται από την κορυφή
είναι το ίχνος του ύψους που άγεται από την κορυφή  . Διερεύνηση.
. Διερεύνηση.Εφαρμογή για

3. Σε τρίγωνο
 οι πλευρές
οι πλευρές 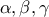 επαληθεύουν τις σχέσεις
επαληθεύουν τις σχέσεις  (1),
(1),  (2)
(2)  όπου
όπου  η ακτίνα του περιγεγραμμένου κύκλου και
η ακτίνα του περιγεγραμμένου κύκλου και  δοθέν μήκος.
δοθέν μήκος. α) Να βρεθούν σε ακτίνια οι τιμές , τις οποίες μπορεί να πάρει η γωνία
 . Να υπολογιστούν συναρτήσει των
. Να υπολογιστούν συναρτήσει των  και
και 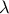 οι γωνίες
οι γωνίες  και
και  του τριγώνου και να προσδιορισθεί ο αριθμός των λύσεων αναλόγως των τιμών του λόγου
του τριγώνου και να προσδιορισθεί ο αριθμός των λύσεων αναλόγως των τιμών του λόγου  .
.β) Έστω
 και
και  δυο άνισα τρίγωνα των οποίων οι πλευρές επαληθεύουν τις σχέσεις (1) και (2). Να αποδείξετε οτι οι γωνίες
δυο άνισα τρίγωνα των οποίων οι πλευρές επαληθεύουν τις σχέσεις (1) και (2). Να αποδείξετε οτι οι γωνίες  και
και  των τριγώνων αυτών αναλόγως των τιμών του λόγου
των τριγώνων αυτών αναλόγως των τιμών του λόγου  επαληθεύουν ή την μια ή την άλλη από τις σειρές των σχέσεων
επαληθεύουν ή την μια ή την άλλη από τις σειρές των σχέσεων  ,
, 
και οτι τα εμβαδά
 και
και  των δυο αυτών τριγώνων ικανοποιούν την εξίσωση
των δυο αυτών τριγώνων ικανοποιούν την εξίσωση  (
( ) όπου το
) όπου το  ή
ή  θα ληφθεί αντίστοιχα αν η γωνία
θα ληφθεί αντίστοιχα αν η γωνία 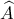 είναι οξεία ή αμβλεία.
είναι οξεία ή αμβλεία.
 τότε
τότε 




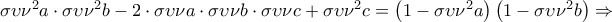

 τότε
τότε 










![2\sigma\upsilon\nu (B-\Gamma)\sigma\upsilon\nu B\sigma\upsilon\nu \Gamma=\sigma\upsilon\nu (B-\Gamma)2\sigma\upsilon\nu B\sigma\upsilon\nu \Gamma=\sigma\upsilon\nu (B-\Gamma)\left [\sigma\upsilon\nu (B-\Gamma)+\sigma\upsilon\nu (B+\Gamma) \right ]= 2\sigma\upsilon\nu (B-\Gamma)\sigma\upsilon\nu B\sigma\upsilon\nu \Gamma=\sigma\upsilon\nu (B-\Gamma)2\sigma\upsilon\nu B\sigma\upsilon\nu \Gamma=\sigma\upsilon\nu (B-\Gamma)\left [\sigma\upsilon\nu (B-\Gamma)+\sigma\upsilon\nu (B+\Gamma) \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/32d9ba9dbd1d9ce59b5fcb35e58299c4.png)















 του
του 


 και έτσι έχουμε ότι
και έτσι έχουμε ότι 
 και ότι
και ότι 
 ,
,  ,
,  και
και 
 και
και  και
και 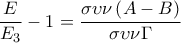






 και ότι
και ότι
 είναι οξυγώνιο.
είναι οξυγώνιο. αμβλεία;
αμβλεία; και ότι
και ότι

![\displaystyle\left (O B\Gamma \right )=\frac{1}{2}\cdot R\cdot R\cdot \eta \mu B\hat{O}\Gamma =\frac{1}{2}\cdot R^{2}\cdot \eta \mu \left [ 2\cdot \left ( 180^{0} \right-A ) \right ]=\frac{1}{2}\cdot \eta \mu \left ( 360^{0} \right-2A )= \displaystyle\left (O B\Gamma \right )=\frac{1}{2}\cdot R\cdot R\cdot \eta \mu B\hat{O}\Gamma =\frac{1}{2}\cdot R^{2}\cdot \eta \mu \left [ 2\cdot \left ( 180^{0} \right-A ) \right ]=\frac{1}{2}\cdot \eta \mu \left ( 360^{0} \right-2A )=](/forum/ext/geomar/texintegr/latexrender/pictures/86d466551b5eaa7ddc24d32bb7a8bf85.png)


 και έτσι έχουμε ότι
και έτσι έχουμε ότι 







 και ότι
και ότι
 αντίστοιχα, έχουμε να αποδείξουμε ότι
αντίστοιχα, έχουμε να αποδείξουμε ότι  Μας λέει κάτι αυτό; Οι παροικούντες την Ιερουσαλήμ (των ανισοτήτων και όχι μόνο) θα αναγνωρίσουν ότι πρόκειται για μια κλασική συνθήκη, η οποία μετασχηματίζεται στην
Μας λέει κάτι αυτό; Οι παροικούντες την Ιερουσαλήμ (των ανισοτήτων και όχι μόνο) θα αναγνωρίσουν ότι πρόκειται για μια κλασική συνθήκη, η οποία μετασχηματίζεται στην 
 .
.