
2. Δίνεται η εξίσωση
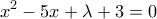 με ρίζες
με ρίζες  .
. Να προσδιορισθεί ο
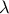 ώστε να είναι
ώστε να είναι 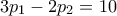 .
.3. Δίνεται το τριώνυμο
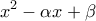 με ρίζες
με ρίζες  .
.Να σχηματισθεί δευτεροβάθμια εξίσωση με ρίζες
 όταν είναι
όταν είναι 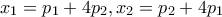

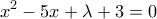 με ρίζες
με ρίζες  .
. 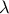 ώστε να είναι
ώστε να είναι 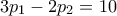 .
.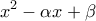 με ρίζες
με ρίζες  .
. όταν είναι
όταν είναι 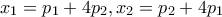
Μεparmenides51 έγραψε:1. Να λυθεί το σύστημα
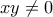 ,
, 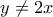 και
και 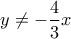 οι εξισώσεις ισοδύναμα γίνονται:
οι εξισώσεις ισοδύναμα γίνονται:
 παίρνουμε:
παίρνουμε: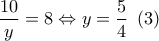

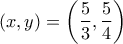 τιμές που επαληθεύουν το σύστημα.
τιμές που επαληθεύουν το σύστημα.Κατ' αρχήν κανένας από τουςparmenides51 έγραψε:1. Να λυθεί το σύστημα
 δεν είναι
δεν είναι  , γιατί δεν επαληθεύει τις εξισώσεις του συστήματος.
, γιατί δεν επαληθεύει τις εξισώσεις του συστήματος. το σύστημα γράφεται ισοδύναμα:
το σύστημα γράφεται ισοδύναμα:


 , απ' όπου βρίσκουμε
, απ' όπου βρίσκουμε 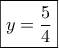
Απόparmenides51 έγραψε: 2. Δίνεται η εξίσωσημε ρίζες
.
Να προσδιορισθεί οώστε να είναι
.
 ισχύει:
ισχύει: 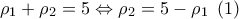
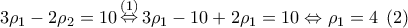
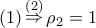

Απόparmenides51 έγραψε: 3. Δίνεται το τριώνυμομε ρίζες
.
Να σχηματισθεί δευτεροβάθμια εξίσωση με ρίζεςόταν είναι
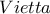 είναι
είναι 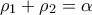 και
και 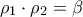
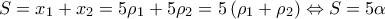
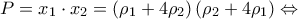

![P = 17{\rho _1}{\rho _2} + 4\left[ {{{\left( {{\rho _1} + {\rho _2}} \right)}^2} - 2{\rho _1}{\rho _2}} \right] \Leftrightarrow P = 17{\rho _1}{\rho _2} + 4\left[ {{{\left( {{\rho _1} + {\rho _2}} \right)}^2} - 2{\rho _1}{\rho _2}} \right] \Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/0157ff811ddd3577f3cd55e85fa98b77.png)


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες