parmenides51 έγραψε: ↑Πέμ Δεκ 19, 2013 10:53 pm
Εξεταστής: Δ. Κορωναίος
4. Να δειχθούν οι ανισότητες
α)

και
β)

όταν

Θα γράψω την λύση γιατί μετά από τόσα χρόνια δεν ασχολήθηκε κάποιος...
Ένας άλλος λόγος είναι για να αναδειχθεί το πόσο πρόχειρη ήταν πολλές φορές η διατύπωση των θεμάτων των εισαγωγικών εξετάσεων...
Ειδικά όταν ο θεματοδότης δεν ήταν μαθηματικός...
Το πρώτο σκέλος είναι η άσκηση 10 στην σελίδα 185 του τρέχοντος σχολικού βιβλίου Άλγεβρας Β' Λυκείου.
Φυσικά στην διατύπωση του σχολικού βιβλίου υπάρχει η συνθήκη

, συνθήκη που ο Δ. Κορωναίος
παρέλειψε να δώσει τότε , το μακρινό 1963...
Ας δούμε την λύση του πρώτου σκέλους.



Η τελευταία ανισότητα ισχύει , άρα ισχύει και η ισοδύναμη σε αυτήν αρχική ανισότητα.
Για το δεύτερο σκέλος , ο Δ. Κορωναίος έπρεπε να δώσει την συνθήκη : οι
 είναι διαφορετικοί μεταξύ τους.
είναι διαφορετικοί μεταξύ τους.
Η απόδειξη της δεύτερης ανισότητας που θα γραφεί παρακάτω γίνεται με την επιπλέον συνθήκη

Αποδείχθηκε προηγουμένως ότι

.
Μπορώ λοιπόν να γράψω άφοβα ότι ισχύει

.
Αν αποδειχθεί ότι
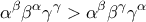
ολοκληρώνεται η απόδειξη.
Η ανισότητα αυτή είναι ισοδύναμη με την


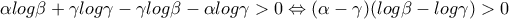
Η τελευταία ανισότητα ισχύει , άρα ισχύει και η ισοδύναμη σε αυτήν αρχική ανισότητα.
Κάτι που μπορεί κάποιος να ρωτήσει , είναι τι γίνεται αν η διάταξη των
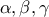
είναι διαφορετική , για παράδειγμα

.
Θα γράψω την λύση για αυτήν την περίπτωση. Θα το κάνω μόνο και μόνο γιατί μας παρακολουθούν μαθητές οι οποίοι δεν θα καταλάβουν αμέσως αν γράψω το τυπικό
'' Ομοίως και οι άλλες περιπτώσεις '' .
Από το πρώτο σκέλος μπορώ να γράψω ότι

κάτι που ισοδυναμεί με
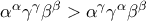
.
Αν αποδειχθεί ότι

ολοκληρώνεται η απόδειξη.
Αν λογαριθμίσω και εφαρμόσω ιδιότητες των λογαρίθμων μπορώ να καταλήξω στην ισοδύναμη ανισότητα

. Aυτή προφανώς ισχύει , άρα και η ισοδύναμη σε αυτήν αρχική ανισότητα.
Νομίζω ότι έγινα σαφής και μπορώ πλέον να γράψω ότι
'' Ομοίως και οι άλλες περιπτώσεις '' .
Λίγες πληροφορίες για τον άνθρωπο που έβαλε την υπογραφή του στα θέματα.
Ο Δ. Κορωναίος ήταν καθηγητής του Ε.Μ.Π. στην έδρα Δομικής Μηχανικής , Οικοδομικών Κατασκευών και Σιδήρου. Είχε τελειώσει πολιτικός μηχανικός στο ίδρυμα που δίδασκε. Η πηγή των πληροφοριών μου δεν γράφει αν είχε διδακτορικό . Μου κάνει εντύπωση ότι οι θεματοδότες των μαθηματικών στις σκληρές εισαγωγικές εξετάσεις του Ε.Μ.Π. σε πολλές περιπτώσεις δεν είχαν σπουδάσει μαθηματικά , ήταν μηχανικοί που είχαν μια έδρα στο ίδρυμα. Πολλοί μου είχαν μιλήσει για το επίπεδο αυτών των θεμάτων , ουδείς μου είπε για αυτούς που τα έθεταν. Οι άνθρωποι αυτοί όμως διαμόρφωναν την κουλτούρα των μαθηματικών των εισαγωγικών εξετάσεων εκείνων των δεκαετιών...
 έχει το
έχει το  τουλάχιστον διπλή ρίζα,
τουλάχιστον διπλή ρίζα,  είναι επίσης ρίζα της εξίσωσης
είναι επίσης ρίζα της εξίσωσης  και το
και το  είναι μια από τις τιμές
είναι μια από τις τιμές 
 όταν
όταν 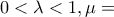 φυσικός
φυσικός και
και  όταν
όταν 

 έχει ρίζα το
έχει ρίζα το  άρα θα ισχύει
άρα θα ισχύει . Επομένως, θα έχουμε
. Επομένως, θα έχουμε 
![\displaystyle{(x-a)(x^2+ax+a^2)-3(x+a)(x-a)-3(x-a)=(x-a)[x^2+(a-3)x+a^2-3a-3]} \displaystyle{(x-a)(x^2+ax+a^2)-3(x+a)(x-a)-3(x-a)=(x-a)[x^2+(a-3)x+a^2-3a-3]}](/forum/ext/geomar/texintegr/latexrender/pictures/bca572f54eb326246761119a4791eeae.png)
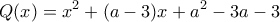 . Αφού το
. Αφού το 
 άρα το
άρα το  και με αντικατάσταση καθεμιάς στην (1) έχουμε
και με αντικατάσταση καθεμιάς στην (1) έχουμε 

 ισοδύναμα έχουμε:
ισοδύναμα έχουμε: 

 παίρνουμε
παίρνουμε 
 και
και  η
η 
 η
η 
 και
και  η
η  και
και  τότε
τότε  και η
και η 

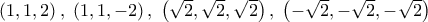 που ικανοποιούν τις εξισώσεις του συστήματος.
που ικανοποιούν τις εξισώσεις του συστήματος. , έχουμε:
, έχουμε: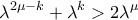 , για κάθε
, για κάθε  (Η ισότητα θα ίσχυε όταν
(Η ισότητα θα ίσχυε όταν  , που αποκλείεται από την υπόθεση)
, που αποκλείεται από την υπόθεση)
 παίρνουμε:
παίρνουμε:




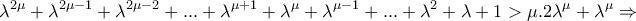


 , συνθήκη που ο Δ. Κορωναίος
, συνθήκη που ο Δ. Κορωναίος


 είναι διαφορετικοί μεταξύ τους.
είναι διαφορετικοί μεταξύ τους. 
 .
.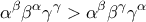 ολοκληρώνεται η απόδειξη.
ολοκληρώνεται η απόδειξη.

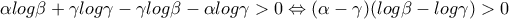
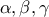 είναι διαφορετική , για παράδειγμα
είναι διαφορετική , για παράδειγμα  .
. κάτι που ισοδυναμεί με
κάτι που ισοδυναμεί με 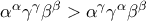 .
. ολοκληρώνεται η απόδειξη.
ολοκληρώνεται η απόδειξη. . Aυτή προφανώς ισχύει , άρα και η ισοδύναμη σε αυτήν αρχική ανισότητα.
. Aυτή προφανώς ισχύει , άρα και η ισοδύναμη σε αυτήν αρχική ανισότητα. . Τότε :
. Τότε : 
 , το οποίο ισχύει , αφού :
, το οποίο ισχύει , αφού :  και
και  .
. , είναι η άμεση εφαρμογή της ανισότητας αναδιάταξης (rearangement inequality, βλέπε
, είναι η άμεση εφαρμογή της ανισότητας αναδιάταξης (rearangement inequality, βλέπε  σε
σε  γράμματα.
γράμματα. έχουν την ίδια διάταξη με τα
έχουν την ίδια διάταξη με τα  , τελειώσαμε.
, τελειώσαμε. ο μικρότερος από τα
ο μικρότερος από τα  , όπως θέλαμε.
, όπως θέλαμε. ο μικρότερος από τα
ο μικρότερος από τα  , όπως θέλαμε.
, όπως θέλαμε. ο μικρότερος από τα
ο μικρότερος από τα  , όπως θέλαμε.
, όπως θέλαμε.