 δυο εξωτερικά εφαπτόμενων κύκλων
δυο εξωτερικά εφαπτόμενων κύκλων  και
και  κέντρων
κέντρων  και
και  κι ακτίνων
κι ακτίνων  και
και  αντίστοιχα, όπου
αντίστοιχα, όπου  , φέρνουμε δυο κάθετες χορδές
, φέρνουμε δυο κάθετες χορδές  και
και  , όπου
, όπου  σημείο του κύκλου
σημείο του κύκλου  και
και  σημείο του κύκλου
σημείο του κύκλου  . Να ορισθεί η θέση των σημείων
. Να ορισθεί η θέση των σημείων  και
και  ώστε να είναι
ώστε να είναι  , όπου
, όπου 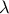 δοθέν ευθύγραμμο τμήμα.
δοθέν ευθύγραμμο τμήμα.2. Θεωρούμε κύκλο διαμέτρου
 κι ακτίνας
κι ακτίνας  . Έστω
. Έστω  η εφαπτομένη του στο σημείο
η εφαπτομένη του στο σημείο  . Εκατέρωθεν της
. Εκατέρωθεν της  φέρνουμε δυο ημιευθείες
φέρνουμε δυο ημιευθείες  και
και  τέτοιες ώστε
τέτοιες ώστε  και
και  \widehat{BAy}=30^o }
\widehat{BAy}=30^o } \displaystyle{Ax}
\displaystyle{Ax} \displaystyle{(\delta) }
\displaystyle{(\delta) } \displaystyle{\Gamma }
\displaystyle{\Gamma } \displaystyle{E}
\displaystyle{E} \displaystyle{Ay}
\displaystyle{Ay} \displaystyle{(\delta)}
\displaystyle{(\delta)} \displaystyle{\Delta}
\displaystyle{\Delta} \displaystyle{H}
\displaystyle{H} \displaystyle{A\Gamma,B\Gamma,\Gamma\Delta, AE,AH}
\displaystyle{A\Gamma,B\Gamma,\Gamma\Delta, AE,AH} \displaystyle{EH}
\displaystyle{EH} \displaystyle{R}
\displaystyle{R} \displaystyle{ \widehat{EZH}}
\displaystyle{ \widehat{EZH}} \displaystyle{Z}
\displaystyle{Z} \displaystyle{E}
\displaystyle{E} \displaystyle{\alpha}
\displaystyle{\alpha} \displaystyle{15^o}$. Να υπολογισθεί ο όγκος και η ολική επιφάνειά της.
\displaystyle{15^o}$. Να υπολογισθεί ο όγκος και η ολική επιφάνειά της.
 \displaystyle{{\rm A}{\rm B}\Gamma }
\displaystyle{{\rm A}{\rm B}\Gamma } \displaystyle{{\rm A}{\rm B} = {\rm B}\Gamma = 2R}
\displaystyle{{\rm A}{\rm B} = {\rm B}\Gamma = 2R} \displaystyle{{\rm A}{\Gamma ^2} = A{B^2} + B{\Gamma ^2} = 8{R^2} \Leftrightarrow A\Gamma = 2R\sqrt 2 }
\displaystyle{{\rm A}{\Gamma ^2} = A{B^2} + B{\Gamma ^2} = 8{R^2} \Leftrightarrow A\Gamma = 2R\sqrt 2 } B\Delta
B\Delta είναι
είναι  και
και . Οπότε
. Οπότε  .
.
 (ως πλευρά τετραγώνου εγγεγραμμένου στον κύκλο).
(ως πλευρά τετραγώνου εγγεγραμμένου στον κύκλο). είναι
είναι 
 . Από νόμο συνημιτόνων στο τρίγωνο
. Από νόμο συνημιτόνων στο τρίγωνο  είναι:
είναι:  . Οπότε
. Οπότε  \displaystyle{R\sqrt {2 + \sqrt 3 } }
\displaystyle{R\sqrt {2 + \sqrt 3 } } \displaystyle{E\widehat ZH = E\widehat AH = {75^0}}$
\displaystyle{E\widehat ZH = E\widehat AH = {75^0}}$ και οι παράπλευρες της έδρες έχουν κλίση προς την βάση ίση με
και οι παράπλευρες της έδρες έχουν κλίση προς την βάση ίση με  . Να υπολογισθεί ο όγκος και η ολική επιφάνειά της.
. Να υπολογισθεί ο όγκος και η ολική επιφάνειά της.







 το απόστημα της κανονικής τετραγωνικής πυραμίδας , το οποίο και θα υπολογίσω.
το απόστημα της κανονικής τετραγωνικής πυραμίδας , το οποίο και θα υπολογίσω.





 της πυραμίδας. Στο σχήμα
της πυραμίδας. Στο σχήμα  είναι η κορυφή της πυραμίδας
είναι η κορυφή της πυραμίδας  τα μέσα δύο απέναντι πλευρών της βάσης και
τα μέσα δύο απέναντι πλευρών της βάσης και  το ύψος της πυραμίδας.
το ύψος της πυραμίδας. τέμνει τη
τέμνει τη  στο
στο  και έστω
και έστω  . Από το ορθογώνιο τρίγωνο
. Από το ορθογώνιο τρίγωνο  με γωνίες
με γωνίες  είναι
είναι  και από Πυθαγόρειο
και από Πυθαγόρειο  .
.



 για να αποφύγω το συμβολισμό
για να αποφύγω το συμβολισμό 
 . Αν οι
. Αν οι  είναι κάθετες στη
είναι κάθετες στη  , ο εντοπισμός των
, ο εντοπισμός των  είναι απλός. Σε κάθε άλλη περίπτωση, αφού οι γωνίες
είναι απλός. Σε κάθε άλλη περίπτωση, αφού οι γωνίες  είναι παραπληρωματικές, η μία είναι οξεία και η άλλη αμβλεία. Χωρίς βλάβη υποθέτω ότι
είναι παραπληρωματικές, η μία είναι οξεία και η άλλη αμβλεία. Χωρίς βλάβη υποθέτω ότι  . Έστω
. Έστω  οι προβολές των
οι προβολές των  . Σκοπός μας είναι να εντοπίσουμε τη θέση του σημείου
. Σκοπός μας είναι να εντοπίσουμε τη θέση του σημείου  να ορίζεται ως το σημείο τομής του κύκλου
να ορίζεται ως το σημείο τομής του κύκλου  με την κάθετη από το
με την κάθετη από το  :
:



 είναι:
είναι: 


 , βρίσκουμε:
, βρίσκουμε:  , που σημαίνει ότι το σημείο
, που σημαίνει ότι το σημείο