 όταν
όταν 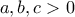
2. Να λυθεί το σύστημα

3. 'Εστω
 . Εαν η εξίσωση αυτή δέχεται οποιοδήποτε ζεύγος ριζών
. Εαν η εξίσωση αυτή δέχεται οποιοδήποτε ζεύγος ριζών  που επαληθεύουν την
που επαληθεύουν την  , να δειχτεί οτι
, να δειχτεί οτι  .
.4. Να δειχτεί η ανισότητα

5. Να εξεταστεί εαν συγκλίνει ή αποκλίνει η ακολουθία
 με
με  και
και 
edit
διόρθωση του τριωνύμου στο 3ο, βιάστηκα




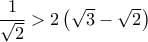


 .
. ισχύει
ισχύει

 έχουμε ότι
έχουμε ότι  και άρα
και άρα


 και τελικά
και τελικά 