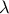 η εξίσωση
η εξίσωση  έχει ρίζες ετερόσημες;
έχει ρίζες ετερόσημες;Να βρεθεί ποια από τις δυο ρίζες είναι κατ' απολύτη τιμή μεγαλύτερη της άλλης.
2. Εαν
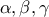 διαδοχικοί όροι γεωμετρικής προόδου, να δείξετε οτι
διαδοχικοί όροι γεωμετρικής προόδου, να δείξετε οτι 
3. Να βρεθεί η συνθήκη ώστε η παράσταση
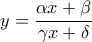 όπου
όπου  ρητοί και
ρητοί και  άρρητος, να είναι ρητή.
άρρητος, να είναι ρητή.
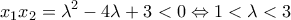
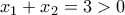 , η θετική ρίζα έχει τη μεγαλύτερη απόλυτη τιμή.
, η θετική ρίζα έχει τη μεγαλύτερη απόλυτη τιμή. ο λόγος της γεωμετρικής προόδου. Τότε θα ισχύει
ο λόγος της γεωμετρικής προόδου. Τότε θα ισχύει  . Αντικαθιστώντας στη δοσμένη έχω:
. Αντικαθιστώντας στη δοσμένη έχω: και αποδείχθηκε.
και αποδείχθηκε.
