1. Εαν
 και
και  τυχαίοι πραγματικοί αριθμοί και
τυχαίοι πραγματικοί αριθμοί και 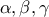 θετικοί αριθμοί,
θετικοί αριθμοί,καθένας από τους οποίους είναι μικρότερος των άλλων δυο,
να δειχθεί οτι
 .
.Επίσης να δειχθεί οτι
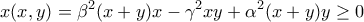
και
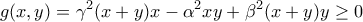 .
.Πότε είναι
 και
και  ;
; Επίσης να δείξετε οτι
 όπου
όπου 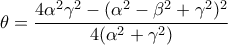
2. α) Δίνεται γεωμετρική πρόοδος με θετικούς όρους.
Να δειχθεί οτι ο μέσος αριθμητικός μέσος του πρώτου και του τελευταίου
είναι πάντοτε μεγαλύτερος του αριθμητικού μέσου όλων των όρων αυτής.
Να εξετάσετε πότε ισχύει το ίσον.
β) Εαν μεταξύ των αριθμών
 και
και  παρεμβάλλουμε
παρεμβάλλουμε  όρους τέτοιους ώστε μαζί με τους
όρους τέτοιους ώστε μαζί με τους  και
και 
να αποτελούν διαδοχικούς όρους αριθμητικής προόδου, και στην συνέχεια μεταξύ των
 και
και 
παρεμβάλλουμε
 όρους τέτοιους ώστε μαζί με τους
όρους τέτοιους ώστε μαζί με τους  και
και  να αποτελούν διαδοχικούς όρους αρμονικής προόδου,
να αποτελούν διαδοχικούς όρους αρμονικής προόδου, να δειχτεί οτι το άθροισμα των γινομένων των ομοταξίων όρων των δυο προόδων διαιρούμενο με
 δίνει πηλίκο
δίνει πηλίκο  .
. Τι περιορισμούς πρέπει να πληρούν τα
 και
και  ;
;3. α) Έστω
 θετικοί αριθμοί και
θετικοί αριθμοί και  . Για
. Για  σχηματίζουμε τους όρους
σχηματίζουμε τους όρους 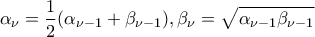 , όπου η ρίζα λαμβάνεται με το θετικό πρόσημο.
, όπου η ρίζα λαμβάνεται με το θετικό πρόσημο. Να δείξετε οτι για κάθε φυσικό
 ισχύουν οι σχέσεις
ισχύουν οι σχέσεις  και
και 
β) Μπορεί ο μιγαδικός αριθμός
 με
με  , να είναι ρίζα της αλγεβρικής εξίσωσης της μορφής
, να είναι ρίζα της αλγεβρικής εξίσωσης της μορφής  , όπου
, όπου  φυσικός και γιατί;
φυσικός και γιατί; Να απαντήσετε επίσης στο ερώτημα <<εφόσον για μιγαδικό
 με
με  , τα σημεία
, τα σημεία που αντιστοιχούν στο μιγαδικό επίπεδο στους αριθμούς
 ορίζουν τρίγωνο,
ορίζουν τρίγωνο, μπορεί αυτό να περιέχει την αρχή
 και γιατί;>>
και γιατί;>>Υ.Γ. Σε μερικές ασκήσεις της εποχής τότε (όπως και στο 3α) αναφέρεται σε τετραγωνική ρίζα με την διατύπωση '' η ρίζα λαμβάνεται με το θετικό πρόσημο''. Τι εννοεί; Μήπως εννοεί οτι από τις δυο τετραγωνικές ρίζες της υπόρριζης ποσότητας, κρατάμε μόνο την θετική; Τότε έλυναν όλες τις εξισώσεις στο
 και δεν υπήρχε κανένας περιορισμός για το υπόρριζο.
και δεν υπήρχε κανένας περιορισμός για το υπόρριζο.edit's
προσθήκη εξεταστή
προσθήκη του θέματος 2β, κατόπιν διασταύρωσης των πηγών της συγκεκριμένης εξέτασης

 ,
,  στές ρίζες , έχει έχει και δύο τετραγωνικές ρίζες.
στές ρίζες , έχει έχει και δύο τετραγωνικές ρίζες.  ή
ή  και
και  ή
ή  , τιμές που προκύπτουν από τον τύπο της
, τιμές που προκύπτουν από τον τύπο της  είναι το
είναι το  " και
" και "
" και
και  για κάθε
για κάθε  φυσικό και
φυσικό και  για κάθε
για κάθε 
 θετικούς και διαφορετικούς μεταξύ τους.
θετικούς και διαφορετικούς μεταξύ τους. για κάθε
για κάθε 

 , με
, με  θετικούς , το παραπάνω συμπέρασμα δεν αλλάζει.
θετικούς , το παραπάνω συμπέρασμα δεν αλλάζει. για κάθε
για κάθε  για κάθε
για κάθε  μπορούμε να γράψουμε ότι
μπορούμε να γράψουμε ότι  για κάθε
για κάθε 







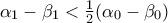
 είναι μεγαλύτερος από τον οποιοδήποτε όρο της
είναι μεγαλύτερος από τον οποιοδήποτε όρο της 
 τυχόντες φυσικοί αριθμοί.
τυχόντες φυσικοί αριθμοί.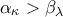
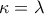

 και επίσης
και επίσης αφού η
αφού η 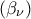 είναι γνησίως αύξουσα , όπως αποδείχθηκε παραπάνω.
είναι γνησίως αύξουσα , όπως αποδείχθηκε παραπάνω.
 αφού η
αφού η 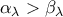
 συγκλίνουν και μάλιστα στον ίδιο πραγματικό αριθμό .
συγκλίνουν και μάλιστα στον ίδιο πραγματικό αριθμό . συγκλίνει σε πραγματικό αριθμό , γιατί είναι γνησίως φθίνουσα και κάτω φραγμένη.
συγκλίνει σε πραγματικό αριθμό , γιατί είναι γνησίως φθίνουσα και κάτω φραγμένη. 
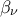 συγκλίνει σε πραγματικό αριθμό , γιατί είναι γνησίως αύξουσα και άνω φραγμένη.
συγκλίνει σε πραγματικό αριθμό , γιατί είναι γνησίως αύξουσα και άνω φραγμένη. 
 το όριο της
το όριο της  το όριο της
το όριο της  , τότε από τον ορισμό της
, τότε από τον ορισμό της  το οποίο ισοδυναμεί με
το οποίο ισοδυναμεί με 
 είναι φθίνουσα, η
είναι φθίνουσα, η  αύξουσα, και
αύξουσα, και  .
.  . ό.έ.δ.
. ό.έ.δ.