parmenides51 έγραψε:Εξετάσεις Αλλοδαπών για τις σχολές ΑΓΡΟΝ(ΟΜΟΙ), ΑΡΧ(ΙΤΕΚΤΟΝΕΣ) , ΜΕΤΑΛΛ(ΕΙΟΛΟΓΟΙ) , ΜΗΧΑΝ(ΟΛΟΓΟΙ), ΠΟΛ(ΙΤΙΚΟΙ), ΤΟΠ(ΟΓΡΑΦΟΙ) , ΧΗΜ(ΙΚΟΙ) ΜΗΧ(ΑΝΙΚΟΙ)
3. Ζητείται να βρεθεί το άθροισμα

των άπειρων όρων της σειράς
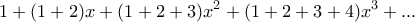
όταν

Πρόκειται για όμορφο θέμα. Η λύση που θα δώσω ίσως δεν είναι η πλέον έξυπνη , όμως θα ωφελήσει τα παιδιά που θα τη μελετήσουν.
Θα βρω κλειστό τύπο για το

.
Iσχύει ότι

Έτσι

 (1)
(1)
Aυτό που θα βρεθεί με κλειστό τύπο είναι το άθροισμα
 Πρόκειται για το άθροισμα
Πρόκειται για το άθροισμα  πρώτων όρων μεικτής προόδου.
πρώτων όρων μεικτής προόδου.
Τι είναι μεικτή πρόοδος;
Είναι μια ακολουθία στην οποία κάθε όρος της είναι γινόμενο δύο ομοτάξιων όρων μιας γεωμετρικής προόδου και μιας αριθμητικής προόδου.
Παραδείγματος χάριν , η ακολουθία
 είναι μεικτή πρόοδος.
είναι μεικτή πρόοδος.
Η πρώτη φορά που είδα αναφορά για μεικτή πρόοδο ήταν όταν ήμουν μαθητής στο άρθρο '' Πρόοδοι '' του Χ.Γκουβιέρου στο τέταρτο τεύχος του '' ΕΥΚΛΕΙΔΗ Β' '' της Ε.Μ.Ε. της περιόδου 1982-1983.
Αυτό που παρουσιάζει ιδιαίτερο ενδιαφέρον είναι ο υπολογισμός του αθροίσματος των  πρώτων όρων μιας μεικτής προόδου.
πρώτων όρων μιας μεικτής προόδου.
Ας το δούμε αυτό στην περίπτωση του

Πολλαπλασιάζουμε με το λόγο

της γεωμετρικής προόδου και έχω

Συνεπώς
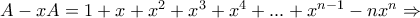


Ας επανέλθουμε τώρα στην
(1). Αυτή γράφεται πλέον

και έτσι βρίσκεται ότι

Είναι γνωστό από τη θεωρία ότι

αφού

.
Με το κριτήριο του λόγου μπορεί εύκολα πλέον να αποδειχθεί ότι

Συνεπώς
 ΜΙΑ ΑΝΑΓΚΑΙΑ ΑΝΑΦΟΡΑ
ΜΙΑ ΑΝΑΓΚΑΙΑ ΑΝΑΦΟΡΑ
Όταν ο Παναγιώτης Χρονόπουλος πριν από δυο χρόνια άρχισε να δημοσιεύει τα παλιά θέματα των εξετάσεων , κάποιοι ίσως θυμήθηκαν τα νεανικά τους χρόνια , κάποιοι άλλοι ίσως τα προσπέρασαν αδιάφορα. Για μένα ήταν η πρώτη φορά που τα έβλεπα σε πλήρη μορφή. Είχα επιτέλους την ευκαιρία να δω αυτά για τα οποία μου μίλαγαν οι παλιοί - όταν ήμουν σχεδόν παιδί - όταν μου περιέγραφαν τις δυσκολίες της καλοκαιρινής προετοιμασίας , την ατελείωτη ύλη , τις μετακινήσεις από το πατρικό σπίτι στην επαρχία στην Αθήνα ή τη Θεσσαλονίκη και ένα σωρό άλλες περιπέτειες από μια εποχή που ένα πτυχίο σήμαινε καταξίωση...
Ο Παναγιώτης Χρονόπουλος στο
http://www.parmenides51.blogspot.com ανεβάζει σταδιακά την πηγή γι αυτόν τον πλούτο θεμάτων , τα ετήσια δελτία του μαθηματικού Αριστείδη Πάλλα , φροντιστού και καθηγητή της Σχολής Ναυτικών Δοκίμων.
Τα βιβλία αυτά '' έσωσαν '' τα θέματα ως την εποχή μας...
Και όχι μόνον των μαθηματικών αλλά και των άλλων μαθημάτων...
Θα ήμουν πολύ μεγάλος ψεύτης αν δεν παραδεχόμουν ότι δεν έκατσα να συγκρίνω κάποιες λύσεις που αναπτύχθηκαν στο forum με τις λύσεις των δελτίων. Σε πολλές περιπτώσεις δεν υπάρχει ουσιαστική διαφορά , σε άλλες όμως οι λύσεις του mathematica δίνουν μια άλλη οπτική γωνία , π.χ. στην παρακάτω
viewtopic.php?f=134&t=40768&p=190141&hi ... B7#p190141
Αποφάσισα οι όποιες δημοσιεύσεις μου στο '' Εξετάσεις Σχολών '' να είναι πλέον τέτοιες που να προσφέρουν κάτι διαφορετικό από τη λύση των δελτίων. Νομίζω ότι αυτό είναι και το πιο έντιμο εκ μέρους μου.
Τηλέμαχος Μπαλτσαβιάς
 και
και  είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης  να δειχθεί η ισότητα
να δειχθεί η ισότητα 
 και ζητείται να υπολογισθεί η τιμή της παράστασης
και ζητείται να υπολογισθεί η τιμή της παράστασης 
 των άπειρων όρων της σειράς
των άπειρων όρων της σειράς 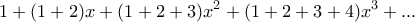 όταν
όταν 
 και
και  είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης  να δειχθεί η ισότητα
να δειχθεί η ισότητα 
 και ζητείται να υπολογισθεί η τιμή της παράστασης
και ζητείται να υπολογισθεί η τιμή της παράστασης 
 των άπειρων όρων της σειράς
των άπειρων όρων της σειράς 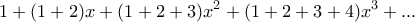 όταν
όταν 
και
είναι οι ρίζες της εξίσωσης
να δειχθεί η ισότητα

 και άρα
και άρα . Η παράσταση γίνεται :
. Η παράσταση γίνεται :
και ζητείται να υπολογισθεί η τιμή της παράστασης



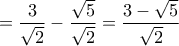




των άπειρων όρων της σειράς
όταν
 .
.

 (1)
(1)
 πρώτων όρων μεικτής προόδου.
πρώτων όρων μεικτής προόδου. είναι μεικτή πρόοδος.
είναι μεικτή πρόοδος. πρώτων όρων μιας μεικτής προόδου.
πρώτων όρων μιας μεικτής προόδου.
 της γεωμετρικής προόδου και έχω
της γεωμετρικής προόδου και έχω
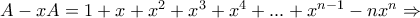




 αφού
αφού  .
.

 , για κάθε
, για κάθε  , πέραν της μεικτής προόδου, είναι ο εξής:
, πέραν της μεικτής προόδου, είναι ο εξής: 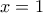 είναι
είναι  .
.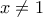 είναι:
είναι: 
 οπότε:
οπότε:  , το οποίο είναι προφανώς ίσο με το
, το οποίο είναι προφανώς ίσο με το  .
.