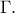3. Να επιλυθεί τρίγωνο  εαν δίνεται
εαν δίνεται  , η διχοτόμος
, η διχοτόμος 
και οτι η διχοτόμος σχηματίζει με την
σχηματίζει με την  οξεία γωνία
οξεία γωνία 
Θα βρούμε το μήκος των πλευρών και τις γωνίες του τριγώνου.
Αν φέρουμε το ύψος

του τριγώνου , τότε το τρίγωνο

είναι ορθογώνιο και ισοσκελές με

.
Αφού

, ισχύει ότι
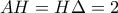

- 1931.png (7.55 KiB) Προβλήθηκε 3539 φορές
Εδώ ας συνεχίσουμε με γεωμετρικές γνώσεις.
Στο τρίγωνο

ισχύει ότι

Στο τρίγωνο

ισχύει ότι

Ισχύει λοιπόν ότι




.
Δηλαδή πρόκειται για
ψευδοορθογώνιο τρίγωνο.
Εδώ να γράψω ότι θεώρησα πως

, και έτσι η

προέκυψε αμβλεία.
Χαρακτηριστική ιδιότητα των τριγώνων αυτών είναι ότι

. Αυτό είναι μια άσκηση Ευκλείδειας Γεωμετρίας της Β' Λυκείου.
Έτσι μπορώ να γράψω ότι

και φυσικά ισχύει ότι

.
Υπολογίζεται πλέον ότι

και

Από το Πυθαγόρειο Θεώρημα στο ορθογώνιο τρίγωνο

προκύπτει ότι

και έτσι

.
Με το ίδιο θεώρημα στο ορθογώνιο τρίγωνο
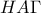
έχω ότι

, κι έτσι
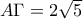
.
Οι πλευρές υπολογίστηκαν , απομένουν οι γωνίες.
Από το ορθογώνιο τρίγωνο
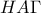
έχω

, και προκύπτει ότι

.
Από το ορθογώνιο τρίγωνο

έχω

.
Άρα

συνεπώς
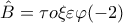
Για να μη γράφω πολλά , από το νόμο του συνημιτόνου μπορώ να βρω ότι

και από δω προκύπτει πλέον και το μέτρο της

.
Αναγνωρίζω ότι ο τρόπος υπολογισμού των γωνιών που προανέφερα δεν είναι ο μόνος , από τη στιγμή που τα μήκη των πλευρών είναι γνωστά.
Ας δούμε και την
ιστορική αξία του θέματος. Στους υπολογισμούς των γωνιών χρησιμοποίησα τις αντίστροφες κυκλικές συναρτήσεις , κάτι που δεν ήταν στη σχολική ύλη το 1931 , ούτε το 2013. Σήμερα , ένα παιδί θα πάει στους πίνακες τριγωνομετρικών αριθμών οξειών γωνιών , και πολύ καλά θα κάνει...
Aν σκεφτούμε κι εμείς έτσι και συμβουλευτούμε το ιστορικής αξίας βιβλίο του Πέτρου Τόγκα '' ΝΕΟΙ ΠΙΝΑΚΕΣ ΛΟΓΑΡΙΘΜΩΝ '' , που περιέχει τους φυσικούς τριγωνομετρικούς αριθμούς με μεγαλύτερη ακρίβεια απ ' ότι οι πίνακες τριγωνομετρικών αριθμών των σχολικών βιβλίων , θα βρούμε ότι
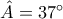
,

,

.
Νομίζω ότι αυτή είναι μια ικανοποιητική απάντηση.
Το 1931 οι υποψήφιοι πήγαιναν στις εξετάσεις με τους πίνακες λογαρίθμων τριγωνομετρικών αριθμών , τους οποίους μπορούσαν να αξιοποιούν κατά τη διάρκεια των εξετάσεων. Πολλοί τόννοι μελάνι χρησιμοποιήθηκαν για την εκτύπωσή τους και άπειρες ώρες διδασκαλίας έγιναν για τη χρήση τους.Και φυσικά αμέτρητος κόπος από την πλευρά των μαθηματικών για τον υπολογισμό τόσων πολλών ψηφίων. Ρωτήστε παλιούς μαθηματικούς να σας πουν....
Το παραπάνω θέμα είχε σκοπό να εξετάσει , εκτός των γνώσεων γεωμετρίας και τριγωνομετρίας , και την ικανότητα των υποψηφίων στη χρήση των λογαρίθμων τριγωνομετρικών αριθμών.
Τη δεκαετία του 1980 σταμάτησε η χρήση και διδασκαλία τους , μια και η εισβολή των Η.Υ. έκανε τα πράγματα απλούστερα, πολύ απλούστερα....
Εδώ και χρόνια τέτοια ζητήματα αντιμετωπίζονται και με τη χρήση ενός scientific calculator.
Αν για ιστορικούς λόγους κάποιος θέλει να δει , τον παραπέμπω στην '' Τριγωνομετρία '' του Ιωάννη Πανάκη , που υπάρχει διαθέσιμη στο internet.
Θέλω να ευχαριστήσω τη Φωτεινή για το σχήμα που έφτιαξε , κατόπιν δικού μου αιτήματος.
 ισχύει
ισχύει  να δείξετε οτι το τρίγωνο είναι ορθογώνιο.
να δείξετε οτι το τρίγωνο είναι ορθογώνιο. και
και 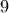 λύσεις του συστήματος
λύσεις του συστήματος 
 ,
,  εαν δίνεται
εαν δίνεται  , η διχοτόμος
, η διχοτόμος 
 σχηματίζει με την
σχηματίζει με την  οξεία γωνία
οξεία γωνία 
 εαν
εαν 

![\displaystyle{\begin{array}{l}
\eta {\mu ^2}A + \eta {\mu ^2}B + \eta {\mu ^2}\Gamma = 2 \Leftrightarrow 2\eta {\mu ^2}A + 2\eta {\mu ^2}B + 2\eta {\mu ^2}\Gamma = 4 \Leftrightarrow \\
\\
\Leftrightarrow 1 - 2\eta {\mu ^2}A + 1 - 2\eta {\mu ^2}B + 1 - 2\eta {\mu ^2}\Gamma = - 1 \Leftrightarrow \\
\\
\Leftrightarrow \sigma \upsilon \nu 2{\rm A} + \sigma \upsilon \nu 2{\rm B} + \sigma \upsilon \nu 2\Gamma = - 1 \Leftrightarrow 2\sigma \upsilon \nu \frac{{2{\rm A} + 2{\rm B}}}{2}\sigma \upsilon \nu \frac{{2{\rm A} - 2{\rm B}}}{2} + 2\sigma \upsilon {\nu ^2}\Gamma - 1 = - 1 \Leftrightarrow \\
\\
\sigma \upsilon \nu ({\rm A} + {\rm B})\sigma \upsilon \nu ({\rm A} - {\rm B}) + \sigma \upsilon {\nu ^2}\Gamma = 0 \Leftrightarrow - \sigma \upsilon \nu \Gamma \sigma \upsilon \nu ({\rm A} - {\rm B}) + \sigma \upsilon {\nu ^2}\Gamma = 0 \Leftrightarrow \\
\\
\Leftrightarrow \sigma \upsilon \nu \Gamma [\sigma \upsilon \nu \Gamma - \sigma \upsilon \nu ({\rm A} - {\rm B})] = 0 \Leftrightarrow \sigma \upsilon \nu \Gamma = 0\,\,\,\, \vee \,\,\,\,\sigma \upsilon \nu \Gamma = \sigma \upsilon \nu ({\rm A} + {\rm B}) \Rightarrow \Gamma = {90^0}\,\, \vee \,\,\,\Gamma = {\rm A} + {\rm B} \Rightarrow \\
\\
\Rightarrow \Gamma = {90^0}\,\, \vee \,\,\,\Gamma = {180^0} - \Gamma \Rightarrow \Gamma = {90^0} \\
\end{array}} \displaystyle{\begin{array}{l}
\eta {\mu ^2}A + \eta {\mu ^2}B + \eta {\mu ^2}\Gamma = 2 \Leftrightarrow 2\eta {\mu ^2}A + 2\eta {\mu ^2}B + 2\eta {\mu ^2}\Gamma = 4 \Leftrightarrow \\
\\
\Leftrightarrow 1 - 2\eta {\mu ^2}A + 1 - 2\eta {\mu ^2}B + 1 - 2\eta {\mu ^2}\Gamma = - 1 \Leftrightarrow \\
\\
\Leftrightarrow \sigma \upsilon \nu 2{\rm A} + \sigma \upsilon \nu 2{\rm B} + \sigma \upsilon \nu 2\Gamma = - 1 \Leftrightarrow 2\sigma \upsilon \nu \frac{{2{\rm A} + 2{\rm B}}}{2}\sigma \upsilon \nu \frac{{2{\rm A} - 2{\rm B}}}{2} + 2\sigma \upsilon {\nu ^2}\Gamma - 1 = - 1 \Leftrightarrow \\
\\
\sigma \upsilon \nu ({\rm A} + {\rm B})\sigma \upsilon \nu ({\rm A} - {\rm B}) + \sigma \upsilon {\nu ^2}\Gamma = 0 \Leftrightarrow - \sigma \upsilon \nu \Gamma \sigma \upsilon \nu ({\rm A} - {\rm B}) + \sigma \upsilon {\nu ^2}\Gamma = 0 \Leftrightarrow \\
\\
\Leftrightarrow \sigma \upsilon \nu \Gamma [\sigma \upsilon \nu \Gamma - \sigma \upsilon \nu ({\rm A} - {\rm B})] = 0 \Leftrightarrow \sigma \upsilon \nu \Gamma = 0\,\,\,\, \vee \,\,\,\,\sigma \upsilon \nu \Gamma = \sigma \upsilon \nu ({\rm A} + {\rm B}) \Rightarrow \Gamma = {90^0}\,\, \vee \,\,\,\Gamma = {\rm A} + {\rm B} \Rightarrow \\
\\
\Rightarrow \Gamma = {90^0}\,\, \vee \,\,\,\Gamma = {180^0} - \Gamma \Rightarrow \Gamma = {90^0} \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/27aec4c89e0e7a4bc1e0e5fbd510782b.png)
 του τριγώνου , τότε το τρίγωνο
του τριγώνου , τότε το τρίγωνο  είναι ορθογώνιο και ισοσκελές με
είναι ορθογώνιο και ισοσκελές με  .
. , ισχύει ότι
, ισχύει ότι 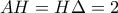

 ισχύει ότι
ισχύει ότι 



 .
. , και έτσι η
, και έτσι η  προέκυψε αμβλεία.
προέκυψε αμβλεία. . Αυτό είναι μια άσκηση Ευκλείδειας Γεωμετρίας της Β' Λυκείου.
. Αυτό είναι μια άσκηση Ευκλείδειας Γεωμετρίας της Β' Λυκείου. και φυσικά ισχύει ότι
και φυσικά ισχύει ότι  .
. και
και 
 προκύπτει ότι
προκύπτει ότι και έτσι
και έτσι  .
.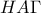 έχω ότι
έχω ότι , κι έτσι
, κι έτσι 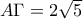 .
. , και προκύπτει ότι
, και προκύπτει ότι  .
. .
. συνεπώς
συνεπώς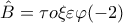
 και από δω προκύπτει πλέον και το μέτρο της
και από δω προκύπτει πλέον και το μέτρο της  .
.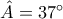 ,
,  ,
,  .
.  κάθετο στην
κάθετο στην  και το
και το  κάθετο στην
κάθετο στην  και
και  προκύπτει εύκολα ότι
προκύπτει εύκολα ότι  και ότι
και ότι  .
. και ότι
και ότι  .
. .
. κάθετη στη
κάθετη στη  είναι ορθογώνιο και έτσι
είναι ορθογώνιο και έτσι  .
. .
. , σύμφωνα με το Πυθαγόρειο Θεώρημα ,
, σύμφωνα με το Πυθαγόρειο Θεώρημα ,

 έχω ότι
έχω ότι 
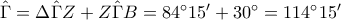
 , βρίσκεται ότι
, βρίσκεται ότι 
 , το μυαλό πάει σε ισόπλευρο τρίγωνο. Έτσι προεκτείνω την
, το μυαλό πάει σε ισόπλευρο τρίγωνο. Έτσι προεκτείνω την  και την
και την  μέχρι να συναντηθούν στο
μέχρι να συναντηθούν στο  .
. , ο υπολογισμός του
, ο υπολογισμός του  μπορεί να γίνει με χρήση του νόμου του συνημιτόνου στο τρίγωνο
μπορεί να γίνει με χρήση του νόμου του συνημιτόνου στο τρίγωνο  .
.
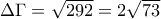 .
.
 , συνεπώς
, συνεπώς  .
. .
. το μέσο της κάθετης πλευράς
το μέσο της κάθετης πλευράς  και
και  το μέσο της κάθετης πλευράς
το μέσο της κάθετης πλευράς 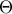 το βαρύκεντρο του τριγώνου
το βαρύκεντρο του τριγώνου 


 προκύπτει ότι
προκύπτει ότι  και έτσι
και έτσι![\displaystyle\varepsilon \varphi \omega =\varepsilon \varphi \left [ 180^{\circ } -\left ( \theta +\varphi \right )\right ]=-\varepsilon \varphi \left ( \theta +\varphi \right )=-\frac{\varepsilon \varphi \theta +\varepsilon \varphi \varphi }{1-\varepsilon \varphi \theta \cdot \varepsilon \varphi \varphi }=\frac{\varepsilon \varphi \theta +\varepsilon \varphi \varphi }{\varepsilon \varphi \theta \cdot \varepsilon \varphi \varphi-1}= \displaystyle\varepsilon \varphi \omega =\varepsilon \varphi \left [ 180^{\circ } -\left ( \theta +\varphi \right )\right ]=-\varepsilon \varphi \left ( \theta +\varphi \right )=-\frac{\varepsilon \varphi \theta +\varepsilon \varphi \varphi }{1-\varepsilon \varphi \theta \cdot \varepsilon \varphi \varphi }=\frac{\varepsilon \varphi \theta +\varepsilon \varphi \varphi }{\varepsilon \varphi \theta \cdot \varepsilon \varphi \varphi-1}=](/forum/ext/geomar/texintegr/latexrender/pictures/12e681fdfdb87faed48abd43ed34481f.png)

 που ισοδυναμεί με
που ισοδυναμεί με 
 της οποίας η διακρίνουσα είναι ίση με
της οποίας η διακρίνουσα είναι ίση με  που είναι ασφαλώς μια θετική ποσότητα.
που είναι ασφαλώς μια θετική ποσότητα.
 είναι οξεία , άρα η εφαπτομένη της είναι θετικός αριθμός , έτσι λοιπόν η αρνητική λύση δεν γίνεται δεκτή.
είναι οξεία , άρα η εφαπτομένη της είναι θετικός αριθμός , έτσι λοιπόν η αρνητική λύση δεν γίνεται δεκτή.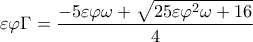
 είναι γνωστή η
είναι γνωστή η  και φυσικά είναι γνωστή και η
και φυσικά είναι γνωστή και η