ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

parmenides51 · #1

1. Θεώρημα τριών καθέτων .

2. Να δειχθεί ότι σε τετράεδρο $\displaystyle{AB\Gamma\Delta}$ με $\displaystyle{ M,N}$ μέσα των $\displaystyle{AB,\Gamma\Delta}$ αντίστοιχα οτι ισχύει
η σχέση $\displaystyle{4MN^2 = A\Delta ^2 + B\Gamma^2 + B\Delta^2 + A\Gamma^2 - AB^2 - \Gamma\Delta^2}$ .
Μετά να δειχθεί οτι αν οι σφαίρες διαμέτρων 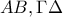$\displaystyle{AB,\Gamma \Delta}$ και οι σφαίρες διαμέτρων $\displaystyle{A\Delta, B\Gamma}$ τέμνονται κάθετα ,
τότε το ίδιο θα συμβαίνει και για τις σφαίρες διαμέτρων 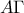$\displaystyle{A\Gamma}$ και $\displaystyle{B\Delta}$ .
Σημείωση : Δύο σφαίρες τέμνονται ορθογώνια όταν το άθροισμα των τετραγώνων των ακτίνων τους ισούται
με το τετράγωνο της διακέντρου τους .

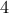3. Δίνεται ευθεία $\displaystyle{(\varepsilon)}$ και $\displaystyle{4}$ διαδοχικά της σημεία $\displaystyle{A,B,\Gamma,\Delta}$ .
Με διαμέτρους $\displaystyle{AB ,\Gamma {\color{red}\Delta} ,A\Delta}$ σχηματίζουμε ημικύκλια στο ένα μέρος της $\displaystyle{(\varepsilon)}$
και με διάμετρο την $\displaystyle{B\Gamma}$ σχηματίζουμε ημικύκλιο στο άλλο μέρος της $\displaystyle{(\varepsilon)}$ .
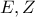Αν $\displaystyle{E,Z}$ είναι τα σημεία τομής του ριζικού άξονα των ημικυκλίων διαμέτρων $\displaystyle{AB ,\Gamma\Delta}$ με τα ημικύκλια διαμέτρων $\displaystyle{A\Delta ,B\Gamma}$
και $\displaystyle{H\Theta}$ είναι η κοινή εφαπτομένη των ημικυκλίων με διαμέτρους $\displaystyle{AB ,\Gamma\Delta}$ να δειχθεί :
α) το 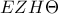$\displaystyle{EZH\Theta}$ είναι ορθογώνιο
β) το εμβαδόν του χωρίου $\displaystyle{AHBZ\Gamma \Theta \Delta E A}$ ισούται με το εμβαδόν κύκλου διαμέτρου $\displaystyle{EZ}$ .

Υ.Γ. Όταν με το καλό βρω και 3η πηγή, θα προσθέσω την ακριβή διατύπωση του 1ου θέματος (ΘΕΩΡΙΑ) όπως είχε ζητηθεί.

edit
Προσθήκη γράμματος στο 3ο

, θενξ Γιώργη

ΚΕΦΑΛΟΝΙΤΗΣ · #2

parmenides51 έγραψε: ↑
Τετ Ιουν 26, 2013 7:31 pm

2. Να δειχθεί ότι σε τετράεδρο $\displaystyle{AB\Gamma\Delta}$ με $\displaystyle{ M,N}$ μέσα των $\displaystyle{AB,\Gamma\Delta}$ αντίστοιχα οτι ισχύει
η σχέση $\displaystyle{4MN^2 = A\Delta ^2 + B\Gamma^2 + B\Delta^2 + A\Gamma^2 - AB^2 - \Gamma\Delta^2}$ .
Μετά να δειχθεί οτι αν οι σφαίρες διαμέτρων $\displaystyle{AB,\Gamma \Delta}$ και οι σφαίρες διαμέτρων $\displaystyle{A\Delta, B\Gamma}$ τέμνονται κάθετα ,
τότε το ίδιο θα συμβαίνει και για τις σφαίρες διαμέτρων $\displaystyle{A\Gamma}$ και $\displaystyle{B\Delta}$ .
Σημείωση : Δύο σφαίρες τέμνονται ορθογώνια όταν το άθροισμα των τετραγώνων των ακτίνων τους ισούται
με το τετράγωνο της διακέντρου τους .

Έστω $M,N,K,\Lambda,Z,E$ τα μέσα των $AB,\Gamma \Delta ,\Delta A,\Gamma B,B\Delta ,A\Gamma$ αντίστοιχα.

Θα εφαρμοστεί ο τύπος που δίνει το μήκος της διαμέσου συναρτήσει των μηκών των πλευρών του τριγώνου.

Στο τρίγωνο $M\Gamma \Delta$ η

είναι διάμεσος. Συνεπώς $\displaystyle MN^{2}=\frac{2M\Gamma ^{2} + 2M\Delta ^{2}-\Gamma \Delta ^{2}}{4}$

Όμως η $M\Gamma$ είναι διάμεσος στο τρίγωνο $AB\Gamma$ και έτσι ισχύει ότι $\displaystyle M\Gamma^{2}=\frac{2A\Gamma ^{2} + 2\Gamma B ^{2}-AB ^{2}}{4}$

Επίσης η $M\Delta$ είναι διάμεσος στο τρίγωνο $AB\Delta$ και έτσι ισχύει ότι $\displaystyle M\Delta^{2}=\frac{2A\Delta ^{2} + 2 \Delta B ^{2}-AB ^{2}}{4}$

Έτσι μπορεί να γραφεί ότι $\displaystyle MN^{2}=\frac{2\frac{2A\Gamma ^{2} + 2\Gamma B ^{2}-AB ^{2}}{4} ^{2} + 2\frac{2A\Delta ^{2} + 2 \Delta B ^{2}-AB ^{2}}{4}-\Gamma \Delta ^{2}}{4}$

και μετά από κάποιες πράξεις και διαδικασίες καταλήγουμε στην ισότητα που θέλει το θέμα,

την $\displaystyle{4MN^2 = A\Delta ^2 + B\Gamma^2 + B\Delta^2 + A\Gamma^2 - AB^2 - \Gamma\Delta^2}$

Νομίζω ότι το το πρώτο υποερώτημα ήταν κάτι εύκολο για τους διαβασμένους υποψηφίους της εποχής...

Ας δούμε και το δεύτερο υποερώτημα...

Oι σφαίρες διαμέτρων

και $\Gamma \Delta$ τέμνονται κάθετα.

Ισχύει λοιπόν ότι $\displaystyle \left ( \frac{AB}{2} \right )^{2} + \left ( \frac{\Gamma \Delta }{2} \right )^{2}=MN^{2}$ που δίνει την ισοδύναμη ισότητα $AB^{2}+\Gamma \Delta ^{2}=4MN^{2}$

Οι σφαίρες διαμέτρων $A\Delta$ και $B\Gamma$ τέμνονται κάθετα.

Ισχύει λοιπόν ότι $\displaystyle \left ( \frac{A\Delta}{2} \right )^{2} + \left ( \frac{B\Gamma }{2} \right )^{2}=K\Lambda ^{2}$ που δίνει την ισοδύναμη ισότητα $A\Delta^{2}+B\Gamma ^{2}=4K\Lambda^{2}$

Αυτό που θέλω να αποδειχθεί είναι η ισότητα $A\Gamma ^{2}+B\Delta ^{2}=4EZ^{2}$

Από το πρώτο υποερώτημα προκύπτει ότι $4EZ^{2}=AB^{2}+B\Gamma ^{2}+\Gamma \Delta ^{2}+\Delta A^{2}-A\Gamma ^{2}-B\Delta ^{2}$

και μπορεί να γραφεί ότι ισχύει $4EZ^{2}=4MN^{2}+4K\Lambda ^{2}-A\Gamma ^{2}-B\Delta ^{2}\Leftrightarrow$

$A\Gamma ^{2}+B\Delta ^{2}=4MN^{2}+4K\Lambda ^{2} - 4EZ^{2}$ (1)

Στο τρίγωνο $AB\Gamma$ ισχύει ότι το $M\Lambda$ είναι παράλληλο με την $A\Gamma$ και ίση με το μισό της.

Στο τρίγωνο $A\Delta \Gamma$ ισχύει ότι το

είναι παράλληλο με την $A\Gamma$ και ίση με το μισό της.

Συνεπώς το $M \Lambda NK$ είναι παραλληλόγραμμο.

Από την Επιπεδομετρία είναι γνωστό ότι: Σε κάθε παραλληλόγραμμο το άθροισμα των τετραγώνων των διαγωνίων του είναι ίσο με το άθροισμα των τετραγώνων των πλευρών του.

Για να μην γίνω πολύ κουραστικός, δεν θα γράψω την απλή απόδειξη του παραπάνω ισχυρισμού. Αν όμως ήμουν υποψήφιος του 1970, θα την έγραφα και μάλιστα πολύ αναλυτικά...
Σε εισαγωγικές εξετάσεις δεν παίζουμε, δεν ρισκάρουμε...

Έτσι λοιπόν έχουμε ότι $MN^{2}+K\Lambda ^{2}=M\Lambda ^{2}+MK^{2}+KN^{2}+N\Lambda ^{2}$

που ισοδυναμεί με $\displaystyle MN^{2}+K\Lambda ^{2}=\left ( \frac{A\Gamma }{2} \right )^{2} +\left ( \frac{B\Delta }{2} \right )^{2}+\left ( \frac{A\Gamma }{2} \right )^{2}+\left ( \frac{B\Delta }{2} \right )^{2}$

που ισοδυναμεί με $4MN^{2}+4K\Lambda ^{2}=2A\Gamma ^{2}+2B\Delta ^{2}$ (2)

H (1) με την βοήθεια της (2) δίνει ότι

$A\Gamma ^{2}+B\Delta ^{2}=4EZ^{2}$

και η πρόταση που θέλαμε να αποδείξουμε έχει αποδειχθεί.

Αφαίρεσα κατόπιν υπόδειξης του Κ.Δόρτσιου μία πρόταση που μπήκε κατά λάθος σε μη σωστή θέση.

Το Ετήσιο Δελτίο του Πάλλα του 1970 στις σελίδες 31 και 32 λύνει το θέμα αυτό.
Στην σελίδα 31, αμέσως μετά την διατύπωση του θέματος, σε παραπομπή γράφει τα εξής:'' Σ.Σ. Το θέμα τούτο δι' άριστον υποψήφιον έχει ανάλυσιν 3 ωρών. Πώς εδόθη;''
Στην σελίδα 32, αμέσως μετά την λύση, γράφει ότι: '' Η σύλληψις και η έκθεσις του θέματος αυτού απαιτεί τουλάχιστον χρόνον 2.30'-3 ωρών από εμπείρους Καθηγητάς ''.

Al.Koutsouridis · #3

parmenides51 έγραψε: ↑
Τετ Ιουν 26, 2013 7:31 pm

2. Να δειχθεί ότι σε τετράεδρο $\displaystyle{AB\Gamma\Delta}$ με $\displaystyle{ M,N}$ μέσα των $\displaystyle{AB,\Gamma\Delta}$ αντίστοιχα οτι ισχύει
η σχέση $\displaystyle{4MN^2 = A\Delta ^2 + B\Gamma^2 + B\Delta^2 + A\Gamma^2 - AB^2 - \Gamma\Delta^2}$ .
Μετά να δειχθεί οτι αν οι σφαίρες διαμέτρων $\displaystyle{AB,\Gamma \Delta}$ και οι σφαίρες διαμέτρων $\displaystyle{A\Delta, B\Gamma}$ τέμνονται κάθετα ,
τότε το ίδιο θα συμβαίνει και για τις σφαίρες διαμέτρων $\displaystyle{A\Gamma}$ και $\displaystyle{B\Delta}$ .
Σημείωση : Δύο σφαίρες τέμνονται ορθογώνια όταν το άθροισμα των τετραγώνων των ακτίνων τους ισούται
με το τετράγωνο της διακέντρου τους .

Το πρώτο ερώτημα με διανύσματα.

$\overrightarrow{NM} =\dfrac{1}{2}\left ( \overrightarrow{DA}+\overrightarrow{DB}-\overrightarrow{DC}\right) \Rightarrow$

$| \overrightarrow{NM} |^2= \dfrac{1}{4}\left( |\overrightarrow{DA}|^2 + |\overrightarrow{DB}|^2+ |\overrightarrow{DC}|^2+2 \overrightarrow{DA} \cdot \overrightarrow{DB} - 2 \overrightarrow{DA} \cdot \overrightarrow{DC} - 2 \overrightarrow{DB} \cdot \overrightarrow{DC}\right)$ ( $\bigstar$ )

'Ομως

$2 \overrightarrow{DA} \cdot \overrightarrow{DB} =|\overrightarrow{DA}|^2 + |\overrightarrow{DB}|^2- |\overrightarrow{AB}|^2$

$2 \overrightarrow{DA} \cdot \overrightarrow{DC} =|\overrightarrow{DA}|^2 + |\overrightarrow{DC}|^2- |\overrightarrow{AC}|^2$

$2 \overrightarrow{DB} \cdot \overrightarrow{DC} =|\overrightarrow{DB}|^2 + |\overrightarrow{DC}|^2- |\overrightarrow{BC}|^2$

Αντικαθιστώντας τις παραπάνω σχέσεις στην ( $\bigstar$ ), βρίσκουμε

$| \overrightarrow{NM} |^2= \dfrac{1}{4}\left( |\overrightarrow{DA}|^2 + |\overrightarrow{BC}|^2+ |\overrightarrow{DB}|^2 + |\overrightarrow{AC}|^2 -|\overrightarrow{DC}|^2 -|\overrightarrow{AB}|^2 \right)$

που είναι το ζητούμενο.

Για το δεύτερο ερώτημα: Αν K,L

είναι τα μέσα των AC, BD

αντίστοιχα και P,Q

τα μέσα τών BC,AD

αντίστοιχα, τότε όμοια με το πρώτο ερώτημα θα έχουμε

4MN^2= DA^2+BC^2+DB^2+AC^2-DC^2-AB^2

Προσθέτοντας κατά μέλη βρίσκουμε ότι

4MN^2+4KL^2+4PQ^2= DA^2+BC^2+DB^2+AC^2+DC^2+AB^2

( $\ast$ )

Όμως από την εκφώνηση

4MN^2= AB^2+CD^2

Οπότε, αφαιρώντας κατά μέλη τις παραπάνω από την ( $\ast$ ), έχουμε

4KL^2= DB^2+AC^2

που είναι ισοδύναμο με το ζητούμενο.

ΚΕΦΑΛΟΝΙΤΗΣ · #4

Οφείλω να παραδεχτώ ότι η λύση του Αλέξανδρου στο 2ο υποερώτημα είναι καλύτερη από την δική μου. Αξιοποιεί πλήρως την ισότητα του 1ου υποερωτήματος, δίχως να ασχολείται με γνώσεις από την Επιπεδομετρία.

#5

ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑
Κυρ Νοέμ 29, 2020 10:54 pm

parmenides51 έγραψε: ↑
Τετ Ιουν 26, 2013 7:31 pm

2. Να δειχθεί ότι σε τετράεδρο $\displaystyle{AB\Gamma\Delta}$ με $\displaystyle{ M,N}$ μέσα των $\displaystyle{AB,\Gamma\Delta}$ αντίστοιχα οτι ισχύει
η σχέση $\displaystyle{4MN^2 = A\Delta ^2 + B\Gamma^2 + B\Delta^2 + A\Gamma^2 - AB^2 - \Gamma\Delta^2}$ .
Μετά να δειχθεί οτι αν οι σφαίρες διαμέτρων $\displaystyle{AB,\Gamma \Delta}$ και οι σφαίρες διαμέτρων $\displaystyle{A\Delta, B\Gamma}$ τέμνονται κάθετα ,
τότε το ίδιο θα συμβαίνει και για τις σφαίρες διαμέτρων $\displaystyle{A\Gamma}$ και $\displaystyle{B\Delta}$ .
Σημείωση : Δύο σφαίρες τέμνονται ορθογώνια όταν το άθροισμα των τετραγώνων των ακτίνων τους ισούται
με το τετράγωνο της διακέντρου τους .
Έστω $M,N,K,\Lambda,Z,E$ τα μέσα των $AB,\Gamma \Delta ,\Delta A,\Gamma B,B\Delta ,A\Gamma$ αντίστοιχα.

Θα εφαρμοστεί ο τύπος που δίνει το μήκος της διαμέσου συναρτήσει των μηκών των πλευρών του τριγώνου.

Στο τρίγωνο $M\Gamma \Delta$ η είναι διάμεσος. Συνεπώς $\displaystyle MN^{2}=\frac{2M\Gamma ^{2} + 2M\Delta ^{2}-\Gamma \Delta ^{2}}{4}$

Όμως η $M\Gamma$ είναι διάμεσος στο τρίγωνο $AB\Gamma$ και έτσι ισχύει ότι $\displaystyle M\Gamma^{2}=\frac{2A\Gamma ^{2} + 2\Gamma B ^{2}-AB ^{2}}{4}$

Επίσης η $M\Delta$ είναι διάμεσος στο τρίγωνο $AB\Delta$ και έτσι ισχύει ότι $\displaystyle M\Delta^{2}=\frac{2A\Delta ^{2} + 2 \Delta B ^{2}-AB ^{2}}{4}$

που με την σειρά της δίνει την ισοδύναμη ισότητα $AB^{2}+\Gamma \Delta ^{2}=4MN^{2}$

Έτσι μπορεί να γραφεί ότι $\displaystyle MN^{2}=\frac{2\frac{2A\Gamma ^{2} + 2\Gamma B ^{2}-AB ^{2}}{4} ^{2} + 2\frac{2A\Delta ^{2} + 2 \Delta B ^{2}-AB ^{2}}{4}-\Gamma \Delta ^{2}}{4}$

και μετά από κάποιες πράξεις και διαδικασίες καταλήγουμε στην ισότητα που θέλει το θέμα,

την $\displaystyle{4MN^2 = A\Delta ^2 + B\Gamma^2 + B\Delta^2 + A\Gamma^2 - AB^2 - \Gamma\Delta^2}$

Νομίζω ότι το το πρώτο υποερώτημα ήταν κάτι εύκολο για τους διαβασμένους υποψηφίους της εποχής...

Ας δούμε και το δεύτερο υποερώτημα...

Oι σφαίρες διαμέτρων και $\Gamma \Delta$ τέμνονται κάθετα.

Ισχύει λοιπόν ότι $\displaystyle \left ( \frac{AB}{2} \right )^{2} + \left ( \frac{\Gamma \Delta }{2} \right )^{2}=MN^{2}$ που δίνει την ισοδύναμη ισότητα $AB^{2}+\Gamma \Delta ^{2}=4MN^{2}$

Οι σφαίρες διαμέτρων $A\Delta$ και $B\Gamma$ τέμνονται κάθετα.

Ισχύει λοιπόν ότι $\displaystyle \left ( \frac{A\Delta}{2} \right )^{2} + \left ( \frac{B\Gamma }{2} \right )^{2}=K\Lambda ^{2}$ που δίνει την ισοδύναμη ισότητα $A\Delta^{2}+B\Gamma ^{2}=4K\Lambda^{2}$

Αυτό που θέλω να αποδειχθεί είναι η ισότητα $A\Gamma ^{2}+B\Delta ^{2}=4EZ^{2}$

Από το πρώτο υποερώτημα προκύπτει ότι $4EZ^{2}=AB^{2}+B\Gamma ^{2}+\Gamma \Delta ^{2}+\Delta A^{2}-A\Gamma ^{2}-B\Delta ^{2}$

και μπορεί να γραφεί ότι ισχύει $4EZ^{2}=4MN^{2}+4K\Lambda ^{2}-A\Gamma ^{2}-B\Delta ^{2}\Leftrightarrow$

$A\Gamma ^{2}+B\Delta ^{2}=4MN^{2}+4K\Lambda ^{2} - 4EZ^{2}$ (1)

Στο τρίγωνο $AB\Gamma$ ισχύει ότι το $M\Lambda$ είναι παράλληλο με την $A\Gamma$ και ίση με το μισό της.

Στο τρίγωνο $A\Delta \Gamma$ ισχύει ότι το είναι παράλληλο με την $A\Gamma$ και ίση με το μισό της.

Συνεπώς το $M \Lambda NK$ είναι παραλληλόγραμμο.

Από την Επιπεδομετρία είναι γνωστό ότι: Σε κάθε παραλληλόγραμμο το άθροισμα των τετραγώνων των διαγωνίων του είναι ίσο με το άθροισμα των τετραγώνων των πλευρών του.

Για να μην γίνω πολύ κουραστικός, δεν θα γράψω την απλή απόδειξη του παραπάνω ισχυρισμού. Αν όμως ήμουν υποψήφιος του 1970, θα την έγραφα και μάλιστα πολύ αναλυτικά...
Σε εισαγωγικές εξετάσεις δεν παίζουμε, δεν ρισκάρουμε...

Έτσι λοιπόν έχουμε ότι $MN^{2}+K\Lambda ^{2}=M\Lambda ^{2}+MK^{2}+KN^{2}+N\Lambda ^{2}$

που ισοδυναμεί με $\displaystyle MN^{2}+K\Lambda ^{2}=\left ( \frac{A\Gamma }{2} \right )^{2} +\left ( \frac{B\Delta }{2} \right )^{2}+\left ( \frac{A\Gamma }{2} \right )^{2}+\left ( \frac{B\Delta }{2} \right )^{2}$

που ισοδυναμεί με $4MN^{2}+4K\Lambda ^{2}=2A\Gamma ^{2}+2B\Delta ^{2}$ (2)

H (1) με την βοήθεια της (2) δίνει ότι

$A\Gamma ^{2}+B\Delta ^{2}=4EZ^{2}$

και η πρόταση που θέλαμε να αποδείξουμε έχει αποδειχθεί.

Το Ετήσιο Δελτίο του Πάλλα του 1970 στις σελίδες 31 και 32 λύνει το θέμα αυτό.
Στην σελίδα 31, αμέσως μετά την διατύπωση του θέματος, σε παραπομπή γράφει τα εξής:'' Σ.Σ. Το θέμα τούτο δι' άριστον υποψήφιον έχει ανάλυσιν 3 ωρών. Πώς εδόθη;''
Στην σελίδα 32, αμέσως μετά την λύση, γράφει ότι: '' Η σύλληψις και η έκθεσις του θέματος αυτού απαιτεί τουλάχιστον χρόνον 2.30'-3 ωρών από εμπείρους Καθηγητάς ''.

Τηλέμαχε καλησπέρα...

Αναρτώ τρία σχήματα με μικρές επικολλημένες ετικέτες που αφορούν
τη λύση σου.(Σ' ευχαριστώ που μου το ζήτησες να το πράξω...)

1ο σχήμα

: Τετράεδρο Πολυτεχνείου 1.png (14.11 KiB) Προβλήθηκε 1483 φορές

Στο σχήμα αυτό εργάζεσαι για το πρώτο ερώτημα.

2ο σχήμα

: Τετράεδρο Πολυτεχνείου 2.png (33.74 KiB) Προβλήθηκε 1483 φορές

Στο σχήμα αυτό εργάζεσαι για το δεύτερο ερώτημα.

3ο σχήμα

: Τετράεδρο Πολυτεχνείου 3.png (68.71 KiB) Προβλήθηκε 1483 φορές

Στο σχήμα αυτό φαίνεται το ένα από τρία ζεύγη των σφαιρών οι οποίες τέμνονται ορθογώνια.
Δηλαδή των σφαιρών με διαμέτρους τις ακμές $\displaystyle{AB}$ και $\displaystyle{\Gamma \Delta}$ .
Μάλιστα στο σχήμα σχεδίασα για του λόγου το αληθές τους δυο αντίστοιχους ισημερινούς
κύκλους των σφαιρών αυτών καθώς επίσης και την γωνία τομής (με κόκκινο χρώμα) αυτών.

Κώστας Δόρτσιος

ΚΕΦΑΛΟΝΙΤΗΣ · #6

Nα ευχαριστήσω τον Κ.Δόρτσιο για μια ακόμη φορά...
Για τα όμορφα σχήματα που αναδεικνύουν το θέμα και τις λύσεις...
Δεν πρέπει να θεωρούμε την προσφορά του Κώστα ως δεδομένη, απαιτείται κόπος και χρόνος.
Θα ήθελα να ευχαριστήσω τον Αλέξανδρο για την πετυχημένη λύση που έγραψε. Αυτήν τη λύση μάλλον δεν την είχε υπ' όψιν του ο Πάλλας...
Και τώρα κάτι που θέλω να γράψω εδώ και λίγες εβδομάδες, ακολουθεί αμέσως...
Ίσως να φαίνομαι αθεράπευτα ρομαντικός ή και οπισθοδρομικός που ασχολούμαι με παλιά θέματα Στερεομετρίας. Κάποιοι θα λένε ότι είμαι εκτός τόπου και χρόνου...
Τις τελευταίες εβδομάδες η κόρη μου παρακολουθεί - φυσικά μέσω υπολογιστή - ένα μάθημα με τίτλο '' Παραστατική και Προοπτική Γεωμετρία '', ένα υποχρεωτικό μάθημα στο πρόγραμμα σπουδών του τμήματος όπου φοιτά. Ο καθηγητής του μαθήματος αυτού έχει τονίσει συχνά την αξία της Στερεομετρίας και την λύπη του για την απουσία της από την μέση εκπαίδευση. Η αξία της Στερεομετρίας έχει τονιστεί από πολλούς καθηγητές ΑΕΙ που εκπαιδεύουν μηχανικούς. Με λίγα λόγια, η Στερεομετρία είναι απαραίτητη...
Απαραίτητη όχι μόνο για όσους θέλουν να ακολουθήσουν σπουδές μηχανικού αλλά και για κάποια θέματα της καθημερινότητας.

Al.Koutsouridis · #7

ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑
Τρί Δεκ 01, 2020 9:53 pm

Ίσως να φαίνομαι αθεράπευτα ρομαντικός ή και οπισθοδρομικός που ασχολούμαι με παλιά θέματα Στερεομετρίας. Κάποιοι θα λένε ότι είμαι εκτός τόπου και χρόνου...

Απαραίτητη όχι μόνο για όσους θέλουν να ακολουθήσουν σπουδές μηχανικού αλλά και για κάποια θέματα της καθημερινότητας.

Ρομαντισμός μπορεί να είναι το να παραθέσουμε μια λύση στο

, το να διδάσκεται και εξετάζεται η στερεομετρία είναι ρεαλισμός για μένα.

ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Re: ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Re: ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Re: ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Re: ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Re: ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Re: ΠΟΛΥΤΕΧΝΙΚΟΣ ΚΥΚΛΟΣ 1970 ΓΕΩΜΕΤΡΙΑ

Μέλη σε σύνδεση