 με ακέραιους συντελεστάς και
με ακέραιους συντελεστάς και  .
. α) να δείξετε ότι
 , όπου
, όπου  πολυώνυμον με άκεραίους συντελεστάς .
πολυώνυμον με άκεραίους συντελεστάς .β) Έστω
 ακέραιος διάφορος του μηδενός και του
ακέραιος διάφορος του μηδενός και του  και η αναδρομική σχέση
και η αναδρομική σχέση 
Να δείξετε ότι o
 είναι πρώτος ως προς τους
είναι πρώτος ως προς τους  .
.2. Έστω
 με ρίζες
με ρίζες  και οι σχέσεις
και οι σχέσεις  και
και  .
.α) Εαν ισχύει μια από τις παραπάνω σχέσεις , να αποδείξετε οτι ισχύει και η άλλη κι αντίστροφα .
β) Εαν ισχύει μια από τις παραπάνω σχέσεις και ισχύει
 , να λύσετε την εξίσωση
, να λύσετε την εξίσωση  .
. 3.΄Έστω συνάρτησις
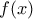 με τιμές στο
με τιμές στο  . Αν ισχύει
. Αν ισχύει  για
για  , τότε
, τότε α) Να δείξετε ότι
 .
.β) Αν
 ρητός άριθμός , να δείξετε ότι
ρητός άριθμός , να δείξετε ότι 
γ) Αν
 ακέραιοι και ισχύει
ακέραιοι και ισχύει  , να δείξετε ότι για ακέραιο
, να δείξετε ότι για ακέραιο 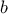 , ο
, ο  είναι ακέραιος.
είναι ακέραιος.edit
προσθήκη αριθμού στο 2β, κάτι υποψιάστηκε ο Δημήτρης

 , να λύσετε την εξίσωση
, να λύσετε την εξίσωση 




 , (δεδομένου ότι δίνεται
, (δεδομένου ότι δίνεται  )
)

 και από προηγουμένως, είδαμε ότι από εδώ έπεται ότι:
και από προηγουμένως, είδαμε ότι από εδώ έπεται ότι:
 ,
, . Parmenides, ξανακοίταξε την πηγή της εκφώνησης, μήπως χρειάζεται κάποια διόρθωση
. Parmenides, ξανακοίταξε την πηγή της εκφώνησης, μήπως χρειάζεται κάποια διόρθωση , ενώ αναζητούμε τις λύσεις της δοσμένης εξίσωσης στο σύνολο
, ενώ αναζητούμε τις λύσεις της δοσμένης εξίσωσης στο σύνολο  των μιγαδικών αριθμών.
των μιγαδικών αριθμών.  , ενώ επί πλέον δίνεται και η
, ενώ επί πλέον δίνεται και η 
 και
και  .
.  , και έχουμε να λύσουμε την εξίσωση:
, και έχουμε να λύσουμε την εξίσωση: 
![\displaystyle{(x-1)[3x^2 +3(a+1)x+a^2 +3a+3]=0} \displaystyle{(x-1)[3x^2 +3(a+1)x+a^2 +3a+3]=0}](/forum/ext/geomar/texintegr/latexrender/pictures/3ab78d23a078a0621c666becdeb68d73.png) .
. 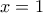 ή
ή 

 και
και 
 των πραγματικών αριθμών, τότε θα έπρεπε να απαιτούσαμε
των πραγματικών αριθμών, τότε θα έπρεπε να απαιτούσαμε  , και οι ρίζες της εξίσωσης θα ήσαν
, και οι ρίζες της εξίσωσης θα ήσαν 
 παίρνουμε
παίρνουμε 
 πράγματι:
πράγματι: 
 :
: ![f(\rho x)=f(x)+f[(\rho -1)x] f(\rho x)=f(x)+f[(\rho -1)x]](/forum/ext/geomar/texintegr/latexrender/pictures/a3f57e887a0f4a200f5218f9a74b6e93.png)
 :
: ![f[(\rho -1) x]=f(x)+f[(\rho -2)x] f[(\rho -1) x]=f(x)+f[(\rho -2)x]](/forum/ext/geomar/texintegr/latexrender/pictures/37afdb1c1780d2ea92ce735389fd674e.png)

 :
: 
![\displaystyle{f(\rho x)+f[(\rho -1)x]+...+f[(\rho -(\rho -2)+1)x]=\mathop\underbrace{f(x)+f(x)+...+f(x)}_{(\rho -3) \; \; o\rho o\iota}+f[(\rho -1)x]+...+f[(\rho -(\rho -2)+1)x] +3f(x) \displaystyle{f(\rho x)+f[(\rho -1)x]+...+f[(\rho -(\rho -2)+1)x]=\mathop\underbrace{f(x)+f(x)+...+f(x)}_{(\rho -3) \; \; o\rho o\iota}+f[(\rho -1)x]+...+f[(\rho -(\rho -2)+1)x] +3f(x)](/forum/ext/geomar/texintegr/latexrender/pictures/7bbe8124f61caee6651a82f0b6a256c2.png)

 με
με  τότε το γινόμενο ακεραίων δε δίνει ακέραιο;
τότε το γινόμενο ακεραίων δε δίνει ακέραιο;
 όταν η
όταν η  είναι
είναι 

 όμως που δίνεται στην εκφώνηση είναι ακέραιος.Δηλαδή αγνοώ τα
όμως που δίνεται στην εκφώνηση είναι ακέραιος.Δηλαδή αγνοώ τα  που δεν είναι ακέραιοι και ορίζω την
που δεν είναι ακέραιοι και ορίζω την  ακεραίων είναι ακέραιος.Σωστά;
ακεραίων είναι ακέραιος.Σωστά;
 ισχύει για κάποια
ισχύει για κάποια  όχι για όλα...
όχι για όλα... για κάθε
για κάθε  (απόδειξη με επαγωγή + περιττή συμμετρία) οπότε
(απόδειξη με επαγωγή + περιττή συμμετρία) οπότε 
 πχ δεν ισχύει για την
πχ δεν ισχύει για την  )
) και
και  :
: 
 άρα
άρα  οπότε
οπότε  τότε
τότε σημαίνει
σημαίνει  δηλαδη
δηλαδη 
 και το ζητούμενο έπεται άμεσα.
και το ζητούμενο έπεται άμεσα.  είναι ακέραιοι στην διαίρεση του
είναι ακέραιοι στην διαίρεση του  με το
με το  εκτελώντας την διαίρεση
εκτελώντας την διαίρεση