Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2022
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1292
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2022
Aς ξεκινήσουμε με το 4ο θέμα...
ΘΕΜΑ Δ
Δίνεται η συνάρτηση με
με
![f\left ( x \right ) =\begin{cases}-x^{3}+3x+1 , -1\leq x\leq 0 \right ] \\ x^{x}, \displaystyle 0< x\leq \frac{2}{e}\end{cases} f\left ( x \right ) =\begin{cases}-x^{3}+3x+1 , -1\leq x\leq 0 \right ] \\ x^{x}, \displaystyle 0< x\leq \frac{2}{e}\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/2567b431a2d76a71de8ca662d538f40e.png)
Δ1. Να αποδείξετε ότι η είναι συνεχής αλλά μη παραγωγίσιμη στο
είναι συνεχής αλλά μη παραγωγίσιμη στο 
MONAΔΕΣ 6
Δ2. i. Nα βρείτε τα κρίσιμα σημεία της (μονάδες 3).
(μονάδες 3).
ii. Nα βρείτε το σύνολο τιμών της (μονάδες 5).
(μονάδες 5).
MONAΔΕΣ 8
Δ3. Να αποδείξετε ότι για κάθε![\displaystyle a, b \epsilon \left [ -1,\frac{2}{e} \right ] \displaystyle a, b \epsilon \left [ -1,\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6df67123ead7c9b834949b8874cb213b.png) υπάρχει
υπάρχει ![\displaystyle\xi \epsilon \left [ -1,\frac{2}{e} \right ] \displaystyle\xi \epsilon \left [ -1,\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b0657f74a479849203a69bf000eded78.png) τέτοιο
τέτοιο
ώστε
MONAΔΕΣ 5
Δ4. Nα αποδείξετε ότι
MONAΔΕΣ 6
ΛΥΣΗ
Δ1.
Φυσικά θεώρησα δεδομένο ότι , αυτό αποδεικνύεται με τον κανόνα De l' Hospital.
, αυτό αποδεικνύεται με τον κανόνα De l' Hospital.

'Αρα
Έτσι η είναι συνεχής στο
είναι συνεχής στο 
Θα εξεταστεί η παραγωγισιμότητα της στο
στο 
![\displaystyle{
\lim_{x\to0^{+}}\frac{f\left ( x \right )-f\left ( 0 \right )}{x-0}=\lim_{x\to0^{+}}\frac{x^{x}-1}{x}=\lim_{x\to0^{+}}\frac{e^{xlnx}-1}{x}=\lim_{x\to0^{+}}\frac{\left ( e^{xlnx}-1 \right )'}{\left ( x \right )'}=\lim_{x\to0^{+}}\left [ \left ( 1+lnx \right )e^{xlnx} \right ]=
\displaystyle{
\lim_{x\to0^{+}}\frac{f\left ( x \right )-f\left ( 0 \right )}{x-0}=\lim_{x\to0^{+}}\frac{x^{x}-1}{x}=\lim_{x\to0^{+}}\frac{e^{xlnx}-1}{x}=\lim_{x\to0^{+}}\frac{\left ( e^{xlnx}-1 \right )'}{\left ( x \right )'}=\lim_{x\to0^{+}}\left [ \left ( 1+lnx \right )e^{xlnx} \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/ce10d089aa9f40818923261a5a6ed4cf.png)
![\left [ 1+\left (-\infty \right ) \right ]\cdot e^{0}=-\infty
\left [ 1+\left (-\infty \right ) \right ]\cdot e^{0}=-\infty](/forum/ext/geomar/texintegr/latexrender/pictures/4ab2dc20e345291241c6e313e94dd676.png)
Έτσι η δεν είναι παραγωγίσιμη στο
δεν είναι παραγωγίσιμη στο 
Δ2.
![f'\left ( x \right ) =\begin{cases}-3x^{2}+3 , -1\leq x< 0 \right ] \\ x^{x}\left ( 1+lnx \right ), \displaystyle 0< x\leq \frac{2}{e}\end{cases} f'\left ( x \right ) =\begin{cases}-3x^{2}+3 , -1\leq x< 0 \right ] \\ x^{x}\left ( 1+lnx \right ), \displaystyle 0< x\leq \frac{2}{e}\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/c73fefce6f5a9d913c8df1755e0db681.png)
Ένα κρίσιμο σημείο για την είναι το
είναι το 
Θα βρεθούν τώρα οι ρίζες της
Για έχω
έχω  και
και 
Φυσικά γίνεται δεκτή μόνο η τιμή
Για έχω
έχω

To είναι κρίσιμο σημείο για την
είναι κρίσιμο σημείο για την 
Το δεν είναι κρίσιμο σημείο της
δεν είναι κρίσιμο σημείο της  , ως άκρο του διαστήματος
, ως άκρο του διαστήματος ![\displaystyle \left [ -1,\frac{2}{e} \right ] \displaystyle \left [ -1,\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/d37101031c496ff4bfe9b53502a5c0b7.png)
στο οποίο ορίζεται η
Aς δούμε και το πεδίο τιμών της
Όπως γνωρίζουμε από τη θεωρία του τριωνύμου δευτέρου βαθμού , ισχύει ότι
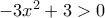 για κάθε
για κάθε  με
με 
Άρα για κάθε
για κάθε 
Aυτό σημαίνει ότι η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\left [ -1,0 \right ] \left [ -1,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/94bb6b1b482e40058b53bfc8275c30ee.png)

Mπορεί να γραφεί ότι![\left [ -1,0 \right ]\rightarrow \left [ -1,1 \right ] \left [ -1,0 \right ]\rightarrow \left [ -1,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2c877117e1d85e76edbdff9916f09fc7.png)
Aς δούμε τι γίνεται για τα για τα οποία
για τα οποία 
Για αυτά ισχύει ότι
 όπως ήδη γράφηκε.
όπως ήδη γράφηκε.
Ισχύει ότι
και ότι
Έχουμε δει ότι και εύκολα βρίσκεται ότι
και εύκολα βρίσκεται ότι
![\displaystyle (0,\frac{1}{e}]\rightarrow [e^{-\frac{1}{e}},1) \displaystyle (0,\frac{1}{e}]\rightarrow [e^{-\frac{1}{e}},1)](/forum/ext/geomar/texintegr/latexrender/pictures/7af68b37580349b58310c4f35dbad44a.png) και
και ![\displaystyle \left [ \frac{1}{e},\frac{2}{e} \right ]\rightarrow \left [ e^{-\frac{1}{e}},\left ( \frac{2}{e} \right )^{\frac{2}{e}} \right ] \displaystyle \left [ \frac{1}{e},\frac{2}{e} \right ]\rightarrow \left [ e^{-\frac{1}{e}},\left ( \frac{2}{e} \right )^{\frac{2}{e}} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/dd6f041e25646abf16822eaecc5999ef.png)
Άρα![\displaystyle (0,\frac{2}{e}]\rightarrow [e^{-\frac{1}{e}},1) \displaystyle (0,\frac{2}{e}]\rightarrow [e^{-\frac{1}{e}},1)](/forum/ext/geomar/texintegr/latexrender/pictures/5531c7e97e85a18cc8fa137374eb0b80.png)
To ζητούμενο πεδίο τιμών, όπως εύκολα καταλαβαίνει κάποιος, είναι το![\left [ -1,1 \right ] \left [ -1,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a0b036fb2288b797367124c31f125474.png)
Δ3.
Πριν γραφεί οτιδήποτε πρέπει να γραφεί ότι η ποσότητα
 βρίσκεται μεταξύ των
βρίσκεται μεταξύ των
 όταν
όταν 
Διακρίνω περιπτώσεις:
1η περίπτωση:
Οι συνθήκες του Θεωρήματος Ενδιαμέσων Τιμών ικανοποιούνται.
Άρα υπάρχει ένα τουλάχιστον τέτοιο ώστε
τέτοιο ώστε 
2η περίπτωση:
Σε αυτήν την περίπτωση
To ζητούμενο είναι το
είναι το  και το
και το 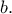
Δ4.
Για κάθε![\displaystyle x \epsilon \left [ \frac{1}{e},\frac{2}{e} \right ] \displaystyle x \epsilon \left [ \frac{1}{e},\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e84cb85782d1a73f3681fab6c02226ba.png) ισχύει ότι
ισχύει ότι 
Άρα ισχύει

Συνεπώς
Φυσικά για τον υπολογισμό του
ελήφθη υπ' όψιν
ότι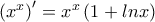
ΘΕΜΑ Δ
Δίνεται η συνάρτηση
 με
με![f\left ( x \right ) =\begin{cases}-x^{3}+3x+1 , -1\leq x\leq 0 \right ] \\ x^{x}, \displaystyle 0< x\leq \frac{2}{e}\end{cases} f\left ( x \right ) =\begin{cases}-x^{3}+3x+1 , -1\leq x\leq 0 \right ] \\ x^{x}, \displaystyle 0< x\leq \frac{2}{e}\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/2567b431a2d76a71de8ca662d538f40e.png)
Δ1. Να αποδείξετε ότι η
 είναι συνεχής αλλά μη παραγωγίσιμη στο
είναι συνεχής αλλά μη παραγωγίσιμη στο 
MONAΔΕΣ 6
Δ2. i. Nα βρείτε τα κρίσιμα σημεία της
 (μονάδες 3).
(μονάδες 3).ii. Nα βρείτε το σύνολο τιμών της
 (μονάδες 5).
(μονάδες 5).MONAΔΕΣ 8
Δ3. Να αποδείξετε ότι για κάθε
![\displaystyle a, b \epsilon \left [ -1,\frac{2}{e} \right ] \displaystyle a, b \epsilon \left [ -1,\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6df67123ead7c9b834949b8874cb213b.png) υπάρχει
υπάρχει ![\displaystyle\xi \epsilon \left [ -1,\frac{2}{e} \right ] \displaystyle\xi \epsilon \left [ -1,\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b0657f74a479849203a69bf000eded78.png) τέτοιο
τέτοιο ώστε

MONAΔΕΣ 5
Δ4. Nα αποδείξετε ότι

MONAΔΕΣ 6
ΛΥΣΗ
Δ1.

Φυσικά θεώρησα δεδομένο ότι
 , αυτό αποδεικνύεται με τον κανόνα De l' Hospital.
, αυτό αποδεικνύεται με τον κανόνα De l' Hospital.
'Αρα

Έτσι η
 είναι συνεχής στο
είναι συνεχής στο 
Θα εξεταστεί η παραγωγισιμότητα της
 στο
στο 
![\displaystyle{
\lim_{x\to0^{+}}\frac{f\left ( x \right )-f\left ( 0 \right )}{x-0}=\lim_{x\to0^{+}}\frac{x^{x}-1}{x}=\lim_{x\to0^{+}}\frac{e^{xlnx}-1}{x}=\lim_{x\to0^{+}}\frac{\left ( e^{xlnx}-1 \right )'}{\left ( x \right )'}=\lim_{x\to0^{+}}\left [ \left ( 1+lnx \right )e^{xlnx} \right ]=
\displaystyle{
\lim_{x\to0^{+}}\frac{f\left ( x \right )-f\left ( 0 \right )}{x-0}=\lim_{x\to0^{+}}\frac{x^{x}-1}{x}=\lim_{x\to0^{+}}\frac{e^{xlnx}-1}{x}=\lim_{x\to0^{+}}\frac{\left ( e^{xlnx}-1 \right )'}{\left ( x \right )'}=\lim_{x\to0^{+}}\left [ \left ( 1+lnx \right )e^{xlnx} \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/ce10d089aa9f40818923261a5a6ed4cf.png)
![\left [ 1+\left (-\infty \right ) \right ]\cdot e^{0}=-\infty
\left [ 1+\left (-\infty \right ) \right ]\cdot e^{0}=-\infty](/forum/ext/geomar/texintegr/latexrender/pictures/4ab2dc20e345291241c6e313e94dd676.png)
Έτσι η
 δεν είναι παραγωγίσιμη στο
δεν είναι παραγωγίσιμη στο 
Δ2.
![f'\left ( x \right ) =\begin{cases}-3x^{2}+3 , -1\leq x< 0 \right ] \\ x^{x}\left ( 1+lnx \right ), \displaystyle 0< x\leq \frac{2}{e}\end{cases} f'\left ( x \right ) =\begin{cases}-3x^{2}+3 , -1\leq x< 0 \right ] \\ x^{x}\left ( 1+lnx \right ), \displaystyle 0< x\leq \frac{2}{e}\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/c73fefce6f5a9d913c8df1755e0db681.png)
Ένα κρίσιμο σημείο για την
 είναι το
είναι το 
Θα βρεθούν τώρα οι ρίζες της

Για
 έχω
έχω  και
και 
Φυσικά γίνεται δεκτή μόνο η τιμή

Για
 έχω
έχω 
To
 είναι κρίσιμο σημείο για την
είναι κρίσιμο σημείο για την 
Το
 δεν είναι κρίσιμο σημείο της
δεν είναι κρίσιμο σημείο της  , ως άκρο του διαστήματος
, ως άκρο του διαστήματος ![\displaystyle \left [ -1,\frac{2}{e} \right ] \displaystyle \left [ -1,\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/d37101031c496ff4bfe9b53502a5c0b7.png)
στο οποίο ορίζεται η

Aς δούμε και το πεδίο τιμών της

Όπως γνωρίζουμε από τη θεωρία του τριωνύμου δευτέρου βαθμού , ισχύει ότι
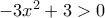 για κάθε
για κάθε  με
με 
Άρα
 για κάθε
για κάθε 
Aυτό σημαίνει ότι η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\left [ -1,0 \right ] \left [ -1,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/94bb6b1b482e40058b53bfc8275c30ee.png)

Mπορεί να γραφεί ότι
![\left [ -1,0 \right ]\rightarrow \left [ -1,1 \right ] \left [ -1,0 \right ]\rightarrow \left [ -1,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2c877117e1d85e76edbdff9916f09fc7.png)
Aς δούμε τι γίνεται για τα
 για τα οποία
για τα οποία 
Για αυτά ισχύει ότι

 όπως ήδη γράφηκε.
όπως ήδη γράφηκε.Ισχύει ότι

και ότι

Έχουμε δει ότι
 και εύκολα βρίσκεται ότι
και εύκολα βρίσκεται ότι ![\displaystyle (0,\frac{1}{e}]\rightarrow [e^{-\frac{1}{e}},1) \displaystyle (0,\frac{1}{e}]\rightarrow [e^{-\frac{1}{e}},1)](/forum/ext/geomar/texintegr/latexrender/pictures/7af68b37580349b58310c4f35dbad44a.png) και
και ![\displaystyle \left [ \frac{1}{e},\frac{2}{e} \right ]\rightarrow \left [ e^{-\frac{1}{e}},\left ( \frac{2}{e} \right )^{\frac{2}{e}} \right ] \displaystyle \left [ \frac{1}{e},\frac{2}{e} \right ]\rightarrow \left [ e^{-\frac{1}{e}},\left ( \frac{2}{e} \right )^{\frac{2}{e}} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/dd6f041e25646abf16822eaecc5999ef.png)
Άρα
![\displaystyle (0,\frac{2}{e}]\rightarrow [e^{-\frac{1}{e}},1) \displaystyle (0,\frac{2}{e}]\rightarrow [e^{-\frac{1}{e}},1)](/forum/ext/geomar/texintegr/latexrender/pictures/5531c7e97e85a18cc8fa137374eb0b80.png)
To ζητούμενο πεδίο τιμών, όπως εύκολα καταλαβαίνει κάποιος, είναι το
![\left [ -1,1 \right ] \left [ -1,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a0b036fb2288b797367124c31f125474.png)
Δ3.
Πριν γραφεί οτιδήποτε πρέπει να γραφεί ότι η ποσότητα
 βρίσκεται μεταξύ των
βρίσκεται μεταξύ των  όταν
όταν 
Διακρίνω περιπτώσεις:
1η περίπτωση:

Οι συνθήκες του Θεωρήματος Ενδιαμέσων Τιμών ικανοποιούνται.
Άρα υπάρχει ένα τουλάχιστον
 τέτοιο ώστε
τέτοιο ώστε 
2η περίπτωση:

Σε αυτήν την περίπτωση

To ζητούμενο
 είναι το
είναι το  και το
και το 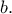
Δ4.
Για κάθε
![\displaystyle x \epsilon \left [ \frac{1}{e},\frac{2}{e} \right ] \displaystyle x \epsilon \left [ \frac{1}{e},\frac{2}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e84cb85782d1a73f3681fab6c02226ba.png) ισχύει ότι
ισχύει ότι 
Άρα ισχύει

Συνεπώς

Φυσικά για τον υπολογισμό του

ελήφθη υπ' όψιν
ότι
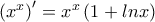
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2022
Δίνω τη γραφική παράσταση τηςΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Παρ Σεπ 01, 2023 8:01 pmAς ξεκινήσουμε με το 4ο θέμα...
ΘΕΜΑ Δ
Δίνεται η συνάρτησημε
Δ1. Να αποδείξετε ότι ηείναι συνεχής αλλά μη παραγωγίσιμη στο
MONAΔΕΣ 6
Δ2. i. Nα βρείτε τα κρίσιμα σημεία της(μονάδες 3).
ii. Nα βρείτε το σύνολο τιμών της(μονάδες 5).
MONAΔΕΣ 8
Δ3. Να αποδείξετε ότι για κάθευπάρχει
τέτοιο
ώστε
MONAΔΕΣ 5
Δ4. Nα αποδείξετε ότι
MONAΔΕΣ 6
ΛΥΣΗ
Δ1.
Φυσικά θεώρησα δεδομένο ότι, αυτό αποδεικνύεται με τον κανόνα De l' Hospital.
'Αρα
Έτσι ηείναι συνεχής στο
Θα εξεταστεί η παραγωγισιμότητα τηςστο
Έτσι ηδεν είναι παραγωγίσιμη στο
Δ2.
Ένα κρίσιμο σημείο για τηνείναι το
Θα βρεθούν τώρα οι ρίζες της
Γιαέχω
και
Φυσικά γίνεται δεκτή μόνο η τιμή
Γιαέχω
Toείναι κρίσιμο σημείο για την
Τοδεν είναι κρίσιμο σημείο της
, ως άκρο του διαστήματος
στο οποίο ορίζεται η
Aς δούμε και το πεδίο τιμών της
Όπως γνωρίζουμε από τη θεωρία του τριωνύμου δευτέρου βαθμού , ισχύει ότι
για κάθε
με
Άραγια κάθε
Aυτό σημαίνει ότι ηείναι γνησίως αύξουσα στο
Mπορεί να γραφεί ότι
Aς δούμε τι γίνεται για ταγια τα οποία
Για αυτά ισχύει ότι
όπως ήδη γράφηκε.
Ισχύει ότι
και ότι
Έχουμε δει ότικαι εύκολα βρίσκεται ότι
και
Άρα
To ζητούμενο πεδίο τιμών, όπως εύκολα καταλαβαίνει κάποιος, είναι το
Δ3.
Πριν γραφεί οτιδήποτε πρέπει να γραφεί ότι η ποσότητα
βρίσκεται μεταξύ των
όταν
Διακρίνω περιπτώσεις:
1η περίπτωση:
Οι συνθήκες του Θεωρήματος Ενδιαμέσων Τιμών ικανοποιούνται.
Άρα υπάρχει ένα τουλάχιστοντέτοιο ώστε
2η περίπτωση:
Σε αυτήν την περίπτωση
To ζητούμενοείναι το
και το
Δ4.
Για κάθεισχύει ότι
Άρα ισχύει
Συνεπώς
Φυσικά για τον υπολογισμό του
ελήφθη υπ' όψιν
ότι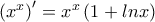
 στη λύση του Τηλέμαχου.
στη λύση του Τηλέμαχου.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
