 .
.Ελάχιστα απλούστερο είναι το :
 , το οποίο επιπλέον μικραίνει το διάστημα .
, το οποίο επιπλέον μικραίνει το διάστημα . .
. , το οποίο επιπλέον μικραίνει το διάστημα .
, το οποίο επιπλέον μικραίνει το διάστημα .emouroukos έγραψε: ↑Δευ Ιουν 06, 2022 5:23 pm.......
Θεωρούμε τη συνάρτηση

με.
Ηείναι παραγωγίσιμη στο
, με
για κάθε.
Είναι:
και
Eπομένως, ηπαρουσιάζει ολικό ελάχιστο στο
. Θα αποδείξουμε ότι
, οπότε θα είναι
για κάθε
και η δοσμένη εξίσωση είναι αδύνατη. Πράγματι, είναι:
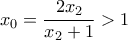 αλλά και
αλλά και 
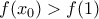 καθώς
καθώς  είναι το ολικό ελάχιστο της
είναι το ολικό ελάχιστο της 
 καθώς η συνάρτηση είναι κυρτή άρα η
καθώς η συνάρτηση είναι κυρτή άρα η  βρίσκεται πάνω από την εφαπτομένη εκτός του σημείου επαφής.
βρίσκεται πάνω από την εφαπτομένη εκτός του σημείου επαφής. 
![f(x)\leq 0 , x \in[x_{1} , x_{2}}] f(x)\leq 0 , x \in[x_{1} , x_{2}}]](/forum/ext/geomar/texintegr/latexrender/pictures/1e215c50de16a9ef7c1ad3be4ca17cf8.png) ,
,  και
και 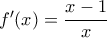 , έχουμε :
, έχουμε : 
![=\displaystyle\left [ xf(x) \right ]_{x_{1}}^{x_{2}}-\int_{x_{2}}^{x_{1}}x\dfrac{x-1}{x}dx =\displaystyle\left [ xf(x) \right ]_{x_{1}}^{x_{2}}-\int_{x_{2}}^{x_{1}}x\dfrac{x-1}{x}dx](/forum/ext/geomar/texintegr/latexrender/pictures/dc71d64fa691f1962b4d5bfe3fdd1d9f.png)
 .
. :
:![h(x)=f(2-x)-f(x)=[2-x-ln(6-3x)]-[x-ln(3x)] h(x)=f(2-x)-f(x)=[2-x-ln(6-3x)]-[x-ln(3x)]](/forum/ext/geomar/texintegr/latexrender/pictures/2fb09af785a623d2dad78b45ee309e4d.png) , για την οποία ισχύει
, για την οποία ισχύει  . Η
. Η  είναι θετική στο
είναι θετική στο 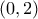 , συνεπώς από την
, συνεπώς από την  προκύπτει η
προκύπτει η  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες